5.2. Линейные алгоритмические процессы

Линейным принято называть вычислительный процесс, в котором операции выполняются последовательно, в порядке их записи. На схеме блоки, отображающие эти операции, располагаются в линейной последовательности.

На рис. 6 показан пример линейного алгоритма, определяющего процесс вычисления арифметического выражения для различных значений переменных.

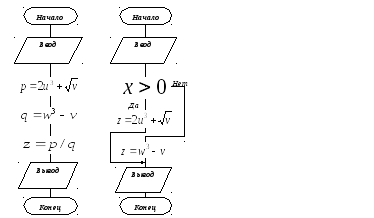
Рис. 6 Рис. 7

5.3. Разветвляющиеся алгоритмические процессы

Вычислительный процесс называется разветвляющимся, если для его реализации предусмотрено несколько направлений (ветвей). Каждое конкретное направление процесса обработки данных является отдельной ветвью вычислений. Ветвление в программе – это выбор одной из нескольких последовательностей команд при выполнении программы. Выбор направления зависит от заранее определенного признака, который может относиться к исходным данным, к промежуточным или конечным результатам. Признак характеризует свойство данных и имеет два или более значений.

Разветвляющийся процесс, включающий в себя две ветви, называется простым, более двух ветвей – сложным. Сложный разветвляющийся процесс можно представить с помощью комбинации простых разветвляющихся процессов. Направление ветвления выбирается логической проверкой, в результате которой возможны два ответа: «да» («+») – условие выполнено и «нет» («–») – условие не выполнено. Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса.

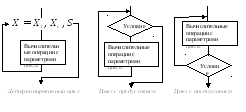
Разветвляющиеся алгоритмические процессы существуют в четырех вариантах:

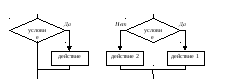НЕПОЛНОЕ ВЕТВЛЕНИЕ ПОЛНОЕ ВЕТВЛЕНИЕ

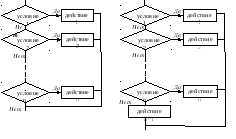
ВЫБОР ВЫБОР-ИНАЧЕ

На рис. 7. показан пример алгоритма ЕСЛИ-ТО-ИНАЧЕ для вычисления следующего выражения:

В зависимости от истинности или ложности условия, указанного в символе «решение», значение функции вычисляется по одному из двух альтернативных выражений.

5.4. Циклические алгоритмические процессы

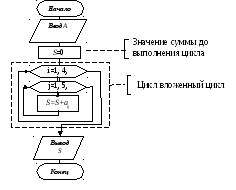
Циклическими называются алгоритмы, содержащие циклы.

Цикл – управляющая структура, организующая многократное выполнение какого-либо действия(действий).

Значения входящих в цикл величин изменяется по мере его повторения. Такие переменные называются параметрами цикла.

Для организации цикла необходимо:

1. задание начальных значений параметров цикла;

2. предусмотреть изменение параметров цикла перед каждым его повторением;

3. проверить условие повторения и завершения цикла;

4. предусмотреть переход в начало цикла, если он не закончен или выход из цикла в противном случае.

Все циклы можно разделить на детерминированные и недетерминированные.

Цикл называется детерминированным, если число повторений тела цикла заранее известно или может быть определено из выражений, в противном случае цикл является недетерминированным.

В детерминированном цикле для управления циклом вводится некоторая переменная для которой задаются начальное значениеи конечное значение, а также шаг– величина на которую изменяется переменная () за каждый цикл. Величинызаписываются в блок «подготовка».

В начале цикла переменной присваивается значение, после чего программа выполняет вычислительные операции с параметрами цикла. Затем программа снова возвращается в блок «подготовка», где переменнаяувеличивается на величину шага, т.е теперьи т. д. До тех пор пока переменнаяне достигнет значения.

Число повторений цикла, определяемое как отношение разности конечного (Х_k) и начального () значений переменной цикла к шагу () плюс один.

В циклах с неизвестным заранее числом повторений различают алгоритмы с предусловием и постусловием.

Для цикла с постусловием тело цикла выполняется как минимум один раз, так как сначала производятся вычисления, а затем проверяется условие выхода из цикла, данному типу циклов соответствует фраза «выполнять действия пока условие истинно (ложно)». В случае цикла с предусловием тело цикла может не выполниться ни разу в случае, если сразу соблюдается условие выхода данный тип циклов можно описать фразой: «Пока условие истинно (ложно) выполнять действия».

После выхода из цикла алгоритм переходит на этап продолжения программы.

Как правило, формулы, обеспечивающие изменение параметров цикла с точки зрения математики «бессмысленны», например, , но без них построение циклов было бы невозможно.

Для того чтобы разобраться в принципах функционирования циклов рассмотрим, что происходит в оперативной памяти компьютера при выполнении программы с циклом.

На определенных участках программы в ней объявляются переменные (в нашем случае Y), для хранения значений этих переменных компьютер выделяет какое-то количество ячеек оперативной памяти, каждая из которых имеет свой уникальный адрес. При обращении программы к переменной компьютер берет ее значение именно из тех ячеек, в которые она была записана. Если на входе выполнения программы переменная меняет свое значение, то из ячеек памяти стирается текущее значение и в них записывается новое. То есть выражение означает, что «новое» значение переменнойY получается путем прибавления к «прошлому» значению переменной Y единицы.

Рассмотрим примеры задач, в решении которых используются циклические структуры.

Пример 1. Найти сумму ряда

Алгоритм решения:

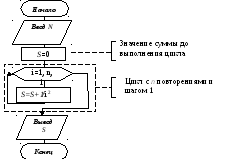
В данном примере был применен детерминированный цикл, т.к. число его повторений было известно из условия задачи.

Пример 2. Определить через, сколько лет размер банковского вклада увеличится в два раза, если начальный вклад составлял K, руб., а процентная ставка N%.

Решение данной задачи возможно двумя способами (рис. 8), вариант а) использует цикл с предусловием, вариант б) цикл с пост условием.

Вложенные циклы. В случае если цикл находится в теле другого цикла, то его называют вложенным. Вложенный цикл по отношению к циклу, в тело которого он вложен, будет именоваться внутренним циклом, и наоборот цикл, в теле которого существует вложенный цикл, будет именоваться внешним по отношению к вложенному. Внутри вложенного цикла в свою очередь может быть вложен еще один цикл, образуя следующий уровень вложенности и так далее. Количество уровней вложенности, как правило, не ограничивается.

На первом проходе, внешний цикл вызывает внутренний, который исполняется до своего завершения, после чего управление передается в тело внешнего цикла. На втором проходе внешний цикл опять вызывает внутренний. И так до тех пор, пока не завершится внешний цикл.

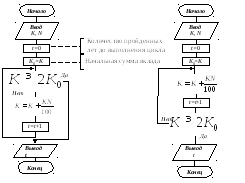
а) б)

Рис. 8

Пример: Найти сумму элементов двумерного массива

Решение:

Строки обозначим индексом i столбцы индексом j.