
- •1 Статистическое наблюдение
- •2 Абсолютные и относительные велечины. Абсолютные статистические величины
- •Относительные статистические величины
- •Виды относительных величин
- •3. Определение относительных величин. Виды относительных величин.
- •5 Ряды распределения их виды и построение
- •6 Понятие задачи и виды статистических группировок
3. Определение относительных величин. Виды относительных величин.
Наряду с абсолютными статистическими величинами большое значение в статистике имеют относительные величины. В процессе выявления ряда важнейших для социально-экономической жизни вопросов возникает необходимость в изучении структуры явления, соотношения между отдельными его частями, развития во времени.
Относительная величина в статистике — это обобщающий показатель, который представляет собой частное от деления одного абсолютного показателя на другой и дает числовую меру соотношения между ними.
Основное условие правильного расчета относительной величины — сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Величина, с которой производится сравнение (знаменатель дроби), обычно называется базой сравнения или основанием.
В зависимости, от выбора базы сравнения относительный показатель может быть представлен в различных долях единицы: десятых; сотых (т. е. процентах); тысячных (десятая часть процента называется промилле); десятитысячных (сотая часть процента называется продецимилле).
По своему содержанию относительные величины подразделяются на виды: относительные величины динамики, планового задания, структуры, интенсивности, уровня экономического развития, координации и сравнения.
1). Относительная величина динамики - она характеризует изменение уровня какого-либо явления во времени и показывает во сколько раз увеличился (или уменьшился) уровень показателя по сравнению с предшествующем периодом.
Различают относительные показатели динамики с постоянной и переменной базой сравнения. Если сравнение осуществляется с одним и тем же базисным уровнем (например, с первым годом рассматриваемого периода), то получают относительные показатели динамики с постоянной базой (базисным).
Если сравнение осуществляется с предшествующим уровнем, то получают показатели динамики с переменной базой (цепным)
 ;
;
 ,
где
,
где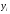 -
это уровень показателей в текущем
(отчетном периоде),
-
это уровень показателей в текущем
(отчетном периоде), -
это уровень показателей в предшествующем
периоде,
-
это уровень показателей в предшествующем
периоде, -
это уровень показателей в базисном
периоде.
-
это уровень показателей в базисном
периоде.
Если данный показатель выраженный в кратком отношении, он называется коэффициентом роста при умножении на 100% получают темп роста.
2). Относительная
величина выполнения плана отражает
фактический уровень показателя в
процентах или коэффициентах по сравнению
с плановым уровнем. Она хар-ет степень
выполнения плана. ,
где
,
где -это
фактический уровень показателя в
отчетном периоде,
-это
фактический уровень показателя в
отчетном периоде, -это
планируемый уровень показателя на
отчетный период.
-это
планируемый уровень показателя на
отчетный период.
3). Относительная величина планового задания характеризует напряженность планового задания. Она показывает на сколько планируется увеличить (или уменьшить) уровень показателя в текущем периоде по сравнению с фактически достигнутым уровнем предшествующего периода.
 ,
где
,
где
 -
это фактический уровень показателя в
базисном периоде.
-
это фактический уровень показателя в
базисном периоде.
4). Относительными
величинами структуры
называются
показатели,
характеризующие долю отдельных частей
изучаемой совокупности
во всем ее объеме.
 ,
где
,
где - это показатель характеризующий i
часть совокупности, сумма
- это показатель характеризующий i
часть совокупности, сумма
 - это показатель по всей совокупности
в целом.
- это показатель по всей совокупности
в целом.
5) Относительная
величина координации характеризует
соотношение между частями одного целого.
Она показывает во сколько раз одна часть
совокупности больше другой или сколько
единиц одной части приходится на 1, 10,
100…1000 и т. д. единиц другой части.
 ,
где
,
где -
это уровень показателей хар-щий часть
совокупности выбранную в качестве базы
сравнения.
-
это уровень показателей хар-щий часть
совокупности выбранную в качестве базы
сравнения.
6). Относительная
величина интенсивности называют
показатель,
характеризующий степень распространения
или уровень развития
того или иного явления в определенной
среде. Они вычисляются
путем сравнения разноименных величин,
находящихся
в определенной связи между собой. Эти
показатели обычно
определяются в расчете на 100, 1000 и т.д.
единиц изучаемой совокупности (на
100 га земли, на 1000 человек населения
и т.д.) и являются именованными числами.
 ,
где
,
где - это показатель характер-ий явления А,
- это показатель характер-ий явления А,
 -
это показатель хар-ий среду распространения
явления А.
-
это показатель хар-ий среду распространения
явления А.
7) Относительная
величина сравнения характеризует
сравнительные размеры одноименных
абсолютных величин относящихся к одному
и тому же периоду или моменту времени,
но к различным объектам или территориям.
 ,
где
,
где -
это показатель хар-ий объект А,
-
это показатель хар-ий объект А, -
показатель хар-ий объект Б.
-
показатель хар-ий объект Б.
12 Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу, любимому занятию в свободное время и т.д. Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Таким образом, величина каждого варианта объективна. Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Средняя величина признака в двух совокупностях может бьпъ одинакрвои, но в одном случае все индивидуальные значения отличаются от нее мало, а в другом — эти отличия велики, т.е. в одном случае вариация признака мала, а в другом - велика, это имеет весьма важное значение для характеристики надежности средней величины. К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации. Самым элементарным показателем вариации признака является размах вариации R, представляющий собой разность между максимальным и минимальным значениями признака: R=Xmax-Xmin
Среднее линейное отклонение d‾ представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта: (х - x‾).
Среднее линейное отклонение: для несгруппированных данных d =∑ | x-x‾| / n
где п — число членов ряда; для сгруппированных данных d‾=∑ | x-x‾| f / ∑ f
где ∑f - сумма частот вариационного ряда.
Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий ( в зависимости от исходных данных):1) простая дисперсия для несгруппированных данных σ2=∑(X-X‾)2 / n 2)взвешенная дисперсия для вариационного ряда σ2=∑(X-X‾)2 f / ∑f Cвойства дисперсии: 1)если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не изменится; 2)если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится или увеличится в i2 раз. Используя второе свойство дисперсии, разделив все варианты на величину интервала, получим следующую формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
![]()
где а — дисперсия, исчисленная по способу моментов; i— величина интервала; x1=x-A/ i новые (преобразованные) значения вариантов
(А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);
— момент второго порядка;
— квадрат момента первого порядка
Среднее квадратическое отклонение σ равно корню квад-| ратному из дисперсии:
для несгруппированных данных
![]()
для вариационного ряда
![]()
Среднее квадратическое отклонение — это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные ва- рианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.
Обозначим: 1 — наличие интересующего нас признака; 0 — его отсутствие; р — доля единиц, обладающих данным признаком; q — доля единиц, не обладающих данным признаком; р + q =1. Исчислим среднее значение альтернативного признака и его дисперсию. Среднее значение альтернативного признака так как p + q = l.,то
![]()
Дисперсия альтернативного признака
![]()
Подст-в в формулу дисперсии q = 1 - р, получим
![]()
Среднее квад-ое отклонение альтерн-ого признака
![]()
Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:: V= σ / X‾ *100
Общая дисперсия σ2 измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака х от общей средней х и может быть вычислена как простая дисперсия
Межгрупповая дисперсия δ 2 характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних X‾i от общей средней X‾ :
![]()
Внутригрупповая (частная) дисперсия σ2 i отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы х) (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
![]()
![]() На
основании внутригрупповой дисперсии
по каждой группе, т.е. на основании
σ2
i
можно
определить общую среднюю
извнутригрупповых дисперсий :
На
основании внутригрупповой дисперсии
по каждой группе, т.е. на основании
σ2
i
можно
определить общую среднюю
извнутригрупповых дисперсий :
![]()
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:
![]()
Внутригрупповые дисперсии показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.) , кроме различий в квалификационном разряд . Средняя из внутригрупповых дисперсий отражает вариацию выработки, обусловленную всеми факторами, кроме квалификации рабочих, но в среднем по всей совокупности. Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп рабочих по квалификационному разряду. Общая дисперсия отражает суммарное влияние всех возможных факторов на общую вариацию среднечасовой выработки изделий всеми рабочими цеха.
Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации ( ή 2 ) — показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
ή 2=δ2 / σ2 Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х (остальная часть общей вариации у обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэф равен 0, а при функциональной связи – единице. Эмпирическое корреляционное отношение — это корень квадратный из эмпирического коэффициента детерминации: v
ή=√ δ2 / σ2 оно показывает тесноту связи между группировочным и результативным признаками.
Эмпирическое корреляционное отношение ή , как и ή 2, может принимать значения от 0 до 1. Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии , т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.
Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
