2.2. Расчет размерной цепи вероятностным методом

2.2.1. Определить коэффициент точности размерной цепи (так как вероятностный метод позволяет расширить допуски по сравнению с методом расчета на максимум-минимум, добавлен индекс «Р»).

,

.

2.2.2. Выбраем значение табличного стандартного коэффициента точности размерной цепи, как ближайшее к рассчитанному .

, [2 с. 42].

Назначаем квалитет для всех составляющих звеньев с неизвестными допусками, соответствующий табличному коэффициенту точности.

IT15, [2 с. 42].

Установить величины допусков размеров составляющих звеньев в соответствии с назначенным квалитетом.

,, ,. [2 с. 7].

2.2.3. Вычисляем коэффициент - определяющий вероятность появления брака по замыкающему звену.

,

.

2.2.4. Проверяем соответствие величины назначенных допусков условию:

,

где -назначенный расширенный допуск составляющего i-го звена.

,

.

2.2.5. Определяем коэффициент риска появления брака по замыкающему звену.

,

где t_H - коэффициент риска для всех составляющих звеньев принимается одинаковый и равный t_H=3, т.к. предполагается, что при получении всех размеров

составляющих звеньев используются технологические процессы, близкие к оптимальным (т.к. данный метод расчета применяется в условиях устоявшегося крупносерийного или массового производства).

.

2.2.6. Определяем вероятный процент брака по замыкающему звену:

т.е. 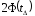-интегральная функция Лапласа, определяемая по

стандартным таблицам [2] с. 45... 46.

,

.

Таблица 2.2 – Расчет размерной цепи методом полной взаимозаменяемости.

Номинальный размер, мм	Обозначение размера	Квалитет	Поле допуска	Допуск размера	Разновидность составляющего звена	Предельные отклонения		Предельные размеры
						верхнее	нижнее	max	min
3		IT15	js15	0,4	увеличивающее	+ 0,2	- 0,2	3,2	2,8
20		IT15	js15	0,84	увеличивающее	+ 0,42	- 0,42	20,42	19,58
30		IT15	js15	0,84	увеличивающее	+ 0,42	- 0,42	30,42	19,58
50		IT15	js15	1	уменьшающее	+ 0,5	- 0,5	50,5	49,5
3		–	–	2,1	замыкающее	+ 1,5	- 0,6	4,5	2,4

2.2.7. Выводы о преимуществах и недостатках обоих методов расчета размерной цепи.

При решении прямой и обратной задач находят применение два метода расчета уравнений размерной цепи: максимума-минимума и вероятностный.

В размерных цепях, в которых должна быть обеспечена полная взаимозаменяемость, допуски рассчитываются по методу максимума-минимума. Методика расчета по этому методу достаточно проста, однако при его использовании предъявляются жесткие требования к точности составляющих звеньев. Такие требования предполагают увеличение затрат на изготовление изделий.

Если по условиям производства целесообразно назначать более широкие допуски на составляющие звенья размерных цепей, допуская при этом выход размеров замыкающего звена за пределы поля допуска у некоторой небольшой части изделий, то следует использовать теоретико-вероятностный метод.