veterinarnia_b_o (1)

1. Термин “информатика” возник:

а) в 40-е годы

б) в 60-е годы

в) в 80-е годы

г) в 90-е годы

2. Информатика – это область человеческой деятельности, связанная …

а) с изобретением и разработкой компьютеров

б) с процессами преобразования информации с помощью компьютеров и их взаимодействием со средой применения

в) только с хранением информации

г) только с применением компьютеров к различным областям науки.

3. Главная функция информатики заключается в …

а) преобразовании информации с помощью компьютеров и их взаимодействии со средой применения

б) разработке компьютерных программ, облегчающих деятельность человека

в) разработке средств хранения информации

г) разработке методов и средств преобразования информации и их использовании в организации технологического процесса переработки информации

4. Информация – это

а) предмет изучения науки информатики

б) знания или сведения о ком-либо или о чем-либо

в) нет точного определения

г) то, что можно хранить в памяти компьютера.

5. Свойством информации НЕ является:

а) дополняемость

б) полнота

в) достоверность

г) эргономичность

6. Носителем информации может быть:

а) любой предмет

б) только бумага

в) только электронные устройства

г) только звук

7. Сигнал называют дискретным, если он …

а) представлен совокупность сигналов различной природы

б) непрерывно изменяется по амплитуде и во времени

в) может принимать лишь конечное число значений в конечном числе моментов времени

г) сообщает об ошибочном действии пользователя

8. Аналоговым называют сигнал, если он

а) представлен совокупность сигналов различной природы

б) непрерывно изменяется по амплитуде и во времени

в) может принимать лишь конечное число значений в конечном числе моментов времени

г) сообщает об ошибочном действии пользователя

9. Информационные системы не обеспечивают

а) сбор информации

б) хранение информации

в) поиск информации

г) анализ и развитие новой информации

10. Процесс, использующий совокупность средств и методов сбора, обработки и передачи данных для получения информации нового качества о состоянии объекта, процесса или явления называется

а) информационным процессом

б) информационной системой

в) информационной технологией

г) процессом переработки информации

11. Первое механическое вычислительное устройство изобрел:

а) Б. Паскаль;

б) Г. Лейбниц;

в) Дж. Байрон;

г) Ч. Бэббидж.

12. Основателем всей современной вычислительной техники считают:

а) Б. Паскаля;

б) Г. Лейбница;

в) Ч. Бэббиджа;

г) Дж. Байрона.

13. Конъюнкция двух высказываний есть истинное высказывание только в том случае, когда:

а) оба высказывания истинны;

б) хотя бы одно из высказываний истинно;

в) только одно из высказываний истинно;

г) оба высказывания ложны.

14. Дизъюнкция двух высказываний есть истинное высказывание только в том случае, когда:

а) оба высказывания истинны;

б) хотя бы одно из высказываний истинно;

в) только одно из высказываний истинно;

г) оба высказывания ложны.

15. В базовую конфигурацию компьютера входят устройства:

а) системный блок и монитор;

б) системный блок, монитор, клавиатура;

в) системный блок, монитор, клавиатура, мышь;

г) системный блок, монитор, клавиатура, мышь, аудио колонки.

16. Периферийными называют:

а) устройства, находящиеся внутри системного блока;

б) только внешние запоминающие устройства;

в) устройства, входящие в базовую конфигурацию компьютера;

г) внешние дополнительные устройства, предназначенные для ввода, вывода и длительного хранения данных.

17. Микропроцессорный комплект (чипсет) – это:

а) микросхема, предназначенная для длительного хранения данных, в том числе и когда компьютер выключен;

б) набор микросхем, управляющих работой внутренних устройств компьютера и определяющих основные функциональные возможности материнской платы;

в) набор микросхем, предназначенных для временного хранения данных, когда компьютер включен;

г) наборы проводников, по которым происходит обмен сигналами между внутренними устройствами компьютера;

18. Шины – это:

а) микросхема, предназначенная для длительного хранения данных, в том числе и когда компьютер выключен;

б) набор микросхем, управляющих работой внутренних устройств компьютера и определяющих основные функциональные возможности материнской платы;

в) набор микросхем, предназначенных для временного хранения данных, когда компьютер включен;

г) наборы проводников, по которым происходит обмен сигналами между внутренними устройствами компьютера;

19. Оперативная память (оперативное запоминающее устройство, ОЗУ) – это:

а) микросхема, предназначенная для длительного хранения данных, в том числе и когда компьютер выключен;

б) набор микросхем, управляющих работой внутренних устройств компьютера и определяющих основные функциональные возможности материнской платы;

в) набор микросхем, предназначенных для временного хранения данных, когда компьютер включен;

г) наборы проводников, по которым происходит обмен сигналами между внутренними устройствами компьютера;

20. ПЗУ (постоянное запоминающее устройство) – это:

а) микросхема, предназначенная для длительного хранения данных, в том числе и когда компьютер выключен;

б) набор микросхем, управляющих работой внутренних устройств компьютера и определяющих основные функциональные возможности материнской платы;

в) набор микросхем, предназначенных для временного хранения данных, когда компьютер включен;

г) наборы проводников, по которым происходит обмен сигналами между внутренними устройствами компьютера.

21. Чему равен 1 байт?

а) 10 бит

б) 10 Кбайт

в) 8 бит

г) 1 бод

22. Чему равен 1 Кбайт?

а) 1000 бит

б) 1000 байт

в) 1024 бит

г) 1024 байт

23. Чему равен 1 Гб?

а) 1024 Мб

б) 1024 Кб

в) байт

г) 1024 бит

24. 48 бит это … байт:

а)

б) 49152

в) 6

г) 384

25. 2 Мб это … Кб

а) 16

б) 2048

в)

г) 2000

26. 4 байта это … бит:

а) 0,5

б) 32

в) 4096

г) 4000

27. 3072 Кб это … Мб

а) 3

б) 384

в) 1024

г) 3145728

28. Число 56 в римской нумерации имеет вид:

а) MVI

б) LIV

в) LVI

г) CVI

29. Число 125 в римской нумерации имеет вид:

а) MXXV

б) LXXV

в) CXVX

г) CXXV

30. Число 2012 в римской нумерации имеет вид:

а) LLXII

б) MMXII

в) CCXII

г) DDXII

31. Число 3624 в римской нумерации имеет вид:

а) MMDCXXIV

б) MMCDXXIV

в) MMDCXXVI

г) MMCDXXVI

32. Число 4444 в римской нумерации имеет вид:

а) MMMMDCLXIV

б) MMMMCDXLIV

в) MMMMCDLXIV

г) MMMMCDXLVI

33. Число CCLX в арабской нумерации имеет вид:

а) 1110

б) 209

в) 240

г) 260

34. Число MCD в арабской нумерации имеет вид:

а) 540

б) 1600

в) 1400

г) 560

35. Число CDXXI в арабской нумерации имеет вид:

а) 921

б) 1121

в) 621

г) 421

36. Число MMMMMDLV в арабской нумерации имеет вид:

а) 5555

б) 555

в) 5455

г) 545

37. Число MMDCXCII в арабской нумерации имеет вид:

а) 2702

б) 2112

в) 2692

г) 2712

38. Число 56 в двоичной системе счисления записывается как:

а) 111

б) 000111

в) 101010

г) 111000

39. Число 75 в двоичной системе счисления записывается как:

а) 1101001

б) 101011

в) 1001011

г) 110101

40. Число 31 в троичной системе счисления записывается как:

а) 1011

б) 1101

в) 121

г) 211

41. Число 56 в троичной системе счисления записывается как:

а) 3233

б) 22

в) 2002

г) 20002

42. Число 74 в восьмеричной системе счисления записывается как:

а) 74

б) 112

в) 211

г) 534

43. Число 100 в восьмеричной системе счисления записывается как:

а) 441

б) 124

в) 100

г) 144

44. Число 54 в шестнадцатеричной системе счисления записывается как:

а) 54

б) 3

в) 63

г) 36

45. Число 572 в шестнадцатеричной системе счисления записывается как:

а) 23В

б) С32

в) 23С

г) В32

46. Число в десятичной с.с. записывается как:

а) 45

б) 61

в) 63

г) 50

47. Число в десятичной с.с. записывается как:

а) 14

б) 112

в) 66

г) 42

48. Число в десятичной с.с. записывается как:

а) 456

б) 71

в) 57

г) 17

49. Число в десятичной с.с. записывается как:

а) 5631

б) 7247

в) 15

г) 5628

50. Минимальным объектом, используемым в текстовом редакторе, является...

а) слово б) точка экрана (пиксель) в) абзац г) символ (знакоместо)

51. В текстовом редакторе при задании параметров страницы устанавливаются...

а)гарнитура, размер, начертание б) отступ, интервал в) поля, ориентация г) стиль, шаблон

52. Чтобы сохранить текстовый файл (документ) в определенном формате, необходимо задать...

а) размер шрифта

б) тип файла

в) параметры абзаца

г) размеры страницы

53. В электронных таблицах выделена группа ячеек А1:ВЗ. Сколько ячеек входит в эту группу?

а) 6

б) 5

в) 4

г) 3

54. В электронных таблицах выделена группа ячеек А1:С2. Сколько ячеек входит в эту группу?

а) 6

б) 5

в) 4

г) 3

55. Ввод формулы в ячейку электронной таблицы начинается со знака:

а) «–»;

б) «+»;

в) «=»;

г) «f(x)».

56. Результатом вычислений в ячейке С1 будет:

	A	B	C
1	10	=A1/2	=A1+B1

а) 20

б) 15

в) 10

г) 5

57. Р

    	A	B	C
    1	5	=A1*2	=A1+B1

    езультатом вычислений в ячейке С1 будет:

а) 5

б) 10

в) 15

г) 20

58. К

    	Название	Площадь, тыс. км2	Население, тыс. чел
    1	Болгария	110,9	8470
    2	Венгрия	93	10300
    3	Испания	504	39100
    4	Люксембург	2,6	392

    акую строку будет занимать запись Болгария после проведения сортировки по возрастанию в поле Площадь, тыс. км²?

а) 1

б) 2

в) 3

г) 4

59. k элементные подмножества n элементного множества, отличающиеся друг от друга или самими элементами или их порядком, называют:

а) размещениями из n элементов по k элементам;

б) сочетаниями из n элементов по k элементам;

в) перестановками из n элементов;

г) элементарными событиями.

60. Множества из n элементов, отличающиеся друг от друга только порядком называют:

а) размещениями из n элементов по k элементам;

б) сочетаниями из n элементов по k элементам;

в) перестановками из n элементов;

г) элементарными событиями.

61. k элементные подмножества n элементного множества, отличающиеся друг от друга хотя бы одним элементом, называют:

а) размещениями из n элементов по k элементам;

б) сочетаниями из n элементов по k элементам;

в) перестановками из n элементов;

г) элементарными событиями.

62. Число размещений из n элементов по k элементам обозначается:

а) ;

б) ;

в) ;

г) .

63. Число размещений из n элементов по k элементам вычисляется по формуле:

а) ;

б) ;

в) ;

г) .

64. Число сочетаний из n элементов по k элементам вычисляется по формуле:

а) ;

б);

в) ;

г) .

65. Число перестановок из n элементов вычисляется по формуле:

а);

б) ;

в) ;

г) .

66. Как перестановки связаны с размещениями?

а) число перестановок из n элементов есть число размещений из n элементов по n элементам;

б) число размещений из n элементов есть число перестановок из n элементов по n элементам;

в) у перестановок и размещений нет связи;

г) нет верного ответа.

67. В классе 30 учащихся. Сколькими способами могут быть выбраны староста и его заместитель, если каждый учащийся может быть выбран на одну из этих должностей?

ОТВЕТ:

68. В седьмом классе изучается 14 предметов. Сколькими способами можно составить расписание занятий на субботу, если в этот день недели должно быть 5 различных уроков?

ОТВЕТ:

69. Сколько различных двухзначных чисел можно составить из цифр 1, 2, 3, 4 при условии, что в каждом числе нет одинаковых цифр?

ОТВЕТ:

70. Для дежурства в классе в течение недели (кроме воскресенья) выделены 6 учащихся. Сколькими способами можно установить очередность дежурств, если каждый учащийся дежурит один раз?

ОТВЕТ:

71. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что в числе цифры не повторяются?

ОТВЕТ:

72. Для проведения экзамена создается комиссия из двух преподавателей. Сколько различных комиссий можно составить из пяти преподавателей?

ОТВЕТ:

73. Сколько экзаменационных комиссий, состоящих из 7 членов, можно образовать из 14 преподавателей?

ОТВЕТ:

74. В чемпионате страны по футболу участвуют 18 команд. Каждые 2 команды играют между собой 1 раз. Сколько матчей сыграно?

ОТВЕТ:

75. Событие, которое не может не произойти и при повторении испытания всякий раз происходит называют:

ОТВЕТ: достоверным

76. Событие, которое не может произойти называют:

ОТВЕТ: невозможным

77. Событие, которое при испытании может произойти, а может не произойти называют:

ОТВЕТ: случайным

78. Вероятность достоверного события равна:

ОТВЕТ:

79. Вероятность невозможного события равна:

ОТВЕТ:

80. Вероятность произвольного события может принимать значение:

а) [0; 1];

б) (1; + )

в) 0;

г) 1.

81. Если при одном испытании появление одного события исключает появление другого, то события называют:

ОТВЕТ: несовместными

82. Если при одном испытании появление одного события не исключает появление другого, то события называют:

ОТВЕТ: совместными

83. При подбрасывании камня событие, состоящее в том, что камень упадет на землю является:

ОТВЕТ: достоверным

84. При одном выстреле по мишени события А = {попадание} и событие B = {промах} являются:

ОТВЕТ: несовместными

85. В ящике 20 шаров 10 белых, 5 красных, 3 голубых, 2 желтых. Наудачу, не глядя, берут 1 шар. Какова вероятность того, что шар окажется белым?

ОТВЕТ:

86. Брошена игральная кость. Какова вероятность события А = {выпавшее число очков четное}?

ОТВЕТ:

87. Талоны занумерованы всеми двузначными числами. Из пачки берут один талон. Какова вероятность того, что номер талона состоит из одинаковых цифр?

ОТВЕТ:

88. В ящике 20 шаров 10 белых, 5 красных, 3 голубых, 2 желтых. Наудачу, не глядя, берут 1 шар. Какова вероятность того, что шар окажется красным?

ОТВЕТ:

89. В ящике 20 шаров 10 белых, 5 красных, 4 голубых, 2 желтых. Наудачу, не глядя, берут 1 шар. Какова вероятность того, что шар окажется голубым?

ОТВЕТ:

90. В ящике 20 шаров 10 белых, 5 красных, 4 голубых, 2 желтых. Наудачу, не глядя, берут 1 шар. Какова вероятность того, что шар окажется желтым?

ОТВЕТ:

91. Событие С, состоящее в наступлении хотя бы одного из событий А или В называют:

а) суммой событий А и В;

б) произведением событий А и В;

в) условной вероятностью события В;

г) разностью событий А и В.

92. Вероятность наступления одного из двух несовместных событий равна:

а) произведению вероятностей этих событий;

б) сумме вероятностей этих событий;

в) разности произведения вероятностей и суммы;

г) сумме вероятностей событий минус вероятность их произведения.

93. Событие С, состоящее в совместном наступлении событий А и В называют:

а) суммой событий А и В;

б) произведением событий А и В;

в) условной вероятностью события В;

г) разностью событий А и В.

94. Вероятность события В при условии, что событие А уже произошло, называется:

а) суммой событий А и В;

б) произведением событий А и В;

в) условной вероятностью события В;

г) разностью событий А и В.

95. Вероятность произведения двух событий равна:

а) произведению вероятностей этих событий;

б) сумме вероятностей этих событий;

в) сумме вероятностей этих событий минус вероятность их произведения;

г) произведению вероятности одного из них на условную вероятность другого.

96. Вероятность произведения независимых событий равна:

а) произведению вероятностей этих событий;

б) сумме вероятностей этих событий;

в) сумме вероятностей этих событий минус вероятность их произведения;

г) произведению вероятности одного из них на условную вероятность другого.

97. Вероятность наступления суммы двух совместных событий равна:

а) произведению вероятностей этих событий;

б) сумме вероятностей этих событий;

в) сумме вероятностей этих событий минус вероятность их произведения;

г) произведению вероятности одного из них на условную вероятность другого.

98. Пусть А – событие, состоящее в том, что выбранная из стада корова имеет годовой удой от 3000 до 3500 кг., В – выбранная из стада корова имеет годовой удой свыше 3500 кг. Что означает событие А + В?

а) выбранная корова имеет годовой удой свыше 3000 кг.;

б) выбранная корова имеет годовой удой свыше 3500 кг.;

в) выбранная корова имеет годовой удой от 3000 до 3500 кг.;

г) выбранная корова имеет годовой удой ниже 3000 кг.

99. В ящике 4 белых, 5 красных, 8 зеленых и 3 голубых шара. Шары перемешиваются и наудачу извлекается один шар. Какова вероятность того, что выбранный шар окажется цветным?

ОТВЕТ:

100. Пусть событие А = {пассажир отправился на вокзал}, В = {пассажир купил билет на поезд}, С = {пассажир сел в поезд}, D = {поезд уехал}. Тогда событие АВСD состоит в том, что:

а) пассажир уехал;

б) поезд уехал;

в) пассажир добрался до вокзала;

г) пассажир сел в поезд.

101. В ящике 60 груш сорта А и 40 груш сорта В. Отбирают 2 груши. Какова вероятность события, что обе груши сорта А?

а) 0,1575;

б) 0,3575;

в) 0,3576;

г) 0,1576.

102. В ящике 60 груш сорта А и 40 груш сорта В. Отбирают 2 груши. Какова вероятность события, что обе груши сорта В?

а) 0,1575;

б) 1;

в) 0,3575;

г) 0,1576.

103. В ящике 60 груш сорта А и 40 груш сорта В. Отбирают 2 груши. Какова вероятность события, что одна груша сорта А, а другая сорта В?

а) 0,4848;

б) 1;

в) 0,2424;

г) 0,4849.

104. Из нижеперечисленных формул выбрать формулу Бернулли:

а) ;

б) ;

в) ;

г)

105. Что показывает формула Бернулли?

а) вероятность события А;

б) вероятность того, что при n испытаниях, событие А произошло k раз;

в) вероятность того, что при k испытаниях, событие А произошло n раз;

г) вероятность произведения событий.

106. Локальная теорема Муавра – Лапласа: если вероятность наступления события А в каждом из n независимых испытаний постоянна и равна p, то справедлива формула:

а) ;

б) ;

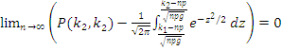в) ;

г) .

107. Следствием из локальной теоремы Муавра – Лапласа является формула:

а);

б) ;

в) ;

г) .

108. Интегральная теорема Муавра – Лапласа: если вероятность наступления события А в каждом из n независимых испытаний постоянна и равна p, то справедлива формула:

а) ;

б) ;

в) ;

г) .

109. Следствием из интегральной теоремы Муавра – Лапласа является формула:

а) ;

б)

в) ;

г) .

110. Функция Лапласа является:

а) нечетной;

б) четной;

в) общего вида;

г) периодической.

111. На опытной делянке посеяно 8 семян. Всхожесть всех семян одинакова и равна 80%. Найти вероятность события, что из 8 посеянных семян взойдет 4, безразлично в какой последовательности:

а) 0,0459;

б) 0,0458;

в) 0,5;

г) 0.

112. На опытной делянке посеяно 8 семян. Всхожесть всех семян одинакова и равна 80%. Найти вероятность события, что из 8 посеянных семян не взойдет ни одно:

а) ;

б) 0,8;

в) 0,0256;

г) 0,1678.

113. На опытной делянке посеяно 8 семян. Всхожесть всех семян одинакова и равна 80%. Найти вероятность события, что из 8 посеянных семян взойдет одно:

а) 0,00008;

б) 0,8;

в) 0,1678;

г) 0,3355.

114. На опытной делянке посеяно 8 семян. Всхожесть всех семян одинакова и равна 80%. Найти вероятность события, что из 8 посеянных семян взойдет 8:

а) 0,1678;

б) 0,8;

в) 1;

г) 0,00000256.

115. Садовод сделал осенью 6 прививок. Известно, что 7 из 10 черенков после зимы остаются жизнеспособными. Найти вероятность события, что 4 черенка прижились?

а) 0,3241;

б) 0,7;

в) 0,2269;

г) 0,6667.

116. Садовод сделал осенью 6 прививок. Известно, что 7 из 10 черенков после зимы остаются жизнеспособными. Найти вероятность события, что 3 черенка прижились?

а) 0,1852;

б) 0,7;

в) 0,5;

г) 0,1853.

117. В лаборатории из партии семян, имеющих всхожесть 90%, высеяно 600 семян. Найти вероятность события, что число семян, давших всходы, не менее 520 и не более 570, если принять, что каждое посеянное зерно взойдет с одной и той же вероятностью Р = 0,9?

а) 1,36;

б) 0,9558;

в) 0,9967;

г) 0,7.

118. Вероятность рождения мальчика p = 0,515. Какова вероятность того, что среди 1000 новорожденных будет 520 мальчиков?