
- •Министерство аграрной политики украины
- •2. Объем курсового проекта
- •3. Порядок выполнения курсового проекта
- •4.Синтез кинематических схем рычажных (стержневых) механизмов.
- •4.4.Синтез кинематической схемы с качающейся кулисой по коэффициенту δ изменеия скорости хода ползуна.
- •4.5.Синтез кинематитческой схемы кривошипно – ползунного механизма по средней скорости ползуна и частоте вращения кривошипа.
- •5.Кинематическое исследование рычажных механизмов
- •5.1.Общие положения
- •5.2.Опеределение перемещений звеньев и траекторий, описываемых точками звеньев.
- •5.3.3.Группа ассура второго класса, третьего вида.
- •5.4.Определение ускорений точек звеньев и угловых ускорения звеньев. (метод планов).
- •5.4.1.Группа ассура второго класса первого вида.
- •5.4.2.Группа ассура второго класса второго вида.
- •5.4.3.Группа ассура второго класса третьего вида.
- •5.5.Построение кинематических диаграмм
- •5.5.1.Построение диаграммы положений.
- •5.5.2.Построение диаграмм скоростей и ускорений.
- •6.Силовой анализ рычажных механизмов.
- •6.1.Общие положения.
- •6.2.Определение сил тяжести и сил инерции.
- •6.3.Силы полезного сопротивления.
- •6.4.Силы в кинематических парах.
- •6.5.Условия статической определимости кинематических цепей и общий порядок силового расчёта.
- •6.6.Силовой расчёт группы ассура второго класса
- •6.7. Силовой расчёт группы ассура второго класса второго вида.
- •6.8. Силовой расчёт группы ассура второго класса третьего вида.
- •6.9. Силовой расчёт входного звена.
- •7.Исследование кулачкового механизма.
- •7.1.Общие положения.
- •7. 2. Синтез кулачкового механизма
- •Из начальных условий (7.6) следует,
- •7.2.2. Синтез профиля кулачка при равноускоренном
- •7.2.3.Синтез профиля кулачка при синусоидальном законе изменения аналога ускорения толкателя.
- •7.2.4. Синтез профиля кулачка при косинусоидальном законе изменеия аналога ускорения толкателя.
- •7.2.5.Выбор минимального радиуса кулачка.
- •7.2.6.Порядок построения профиля кулачка.
- •7.3.2. Экспериментальное уравновешивание
- •7.3.3.Определение значения уравновешивающей
- •8. Исследование зубчатых передач
- •8.1. Общие положения
- •8.2. Зубчатые передачи с неподвижными осями.
- •8.2.1.Синтез зубчатых передач с неподвижными осями.
- •8.4.Зубчатые передачи с подвижными осями.
- •8.3.1 Синтез планетарных зубчатых передач.
- •Условие соосности.
- •Условие отсутствия подрезания и интерференции зубьев.
- •Условие соседства.
- •Условие сборки.
- •8.3. Определение линейных скоростей точек звеньев у планетарных зубчатых передач.
- •9.Задания на курсовое проектирование.
- •Продолжение таблицы 9.1
- •Приложение 1
- •Список литературы
5.3.3.Группа ассура второго класса, третьего вида.
Рассмотрим построение плана скоростей для группы, изображенной ена рис. 5.6.
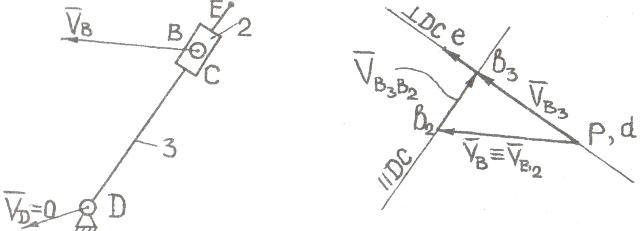
Рис. 5.6 Рис.5.7
Группа Асура (5.6) состоит из двух звеньев и двух вращательных (крайних) кинематических пар В, Dи внутренней поступательной кинематической пары С.
Отметим, что в точке В мгновенно совпадает точка В2принадлежащая звену 2 и точка В3относительно точке В2, из уравнения (5.1) найдётся
![]() ,
(5.8)
,
(5.8)
А скорость
![]() относительно точкиDопределится
относительно точкиDопределится
![]() (5.9)
(5.9)
Приравнивая правые части уравнений (5.8) и (5.9), имеем
![]() (5.10)
(5.10)
В уравнении (5.10) положим, что
![]() , тогда
, тогда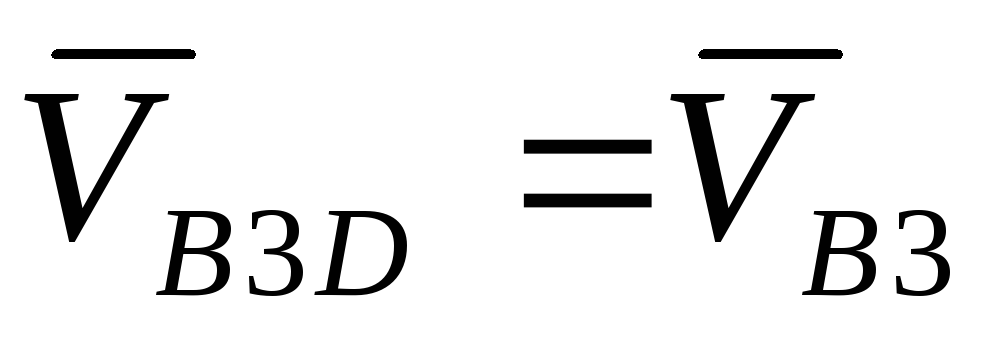 .
.
Выбрав масштаб
![]() , построим план скоростей (рис.5.7),
соответствующий уравнению (5.10). Из полюса
р проводим отрезок рв2, изображающий
в масштабе
, построим план скоростей (рис.5.7),
соответствующий уравнению (5.10). Из полюса
р проводим отрезок рв2, изображающий
в масштабе![]() скорость
скорость![]() .
.
Вектор скорости ползуна 2 относительно
кулисы 3
![]() направлен вдоль кулисы. В соответствии
с левой частью уравнения (5.10) из точки
в2плана скоростей проводим линию,
параллельную кулисе. Точка В3,
принадлежащая кулисе относительно
точкиDсовершает
вращательное движение, так как в точкеDрасположена вращательная
кинематическая пара, поэтому вектор
скорости
направлен вдоль кулисы. В соответствии
с левой частью уравнения (5.10) из точки
в2плана скоростей проводим линию,
параллельную кулисе. Точка В3,
принадлежащая кулисе относительно
точкиDсовершает
вращательное движение, так как в точкеDрасположена вращательная
кинематическая пара, поэтому вектор
скорости![]() направлен перпендикулярно кулисе 3.
Через точку р проводим линию,
перпендикулярную направлению кулисы
3. В точке в3в соответствии с
уравнением (5.10) сойдутся векторы рв3,
в2в3. Значение скорости
направлен перпендикулярно кулисе 3.
Через точку р проводим линию,
перпендикулярную направлению кулисы
3. В точке в3в соответствии с
уравнением (5.10) сойдутся векторы рв3,
в2в3. Значение скорости![]() найдётся
найдётся![]() найдётся
найдётся![]() .
.
Угловая скорость кулисы 3 определится
![]()
где
![]() - расстояние между точкамиDи В3звенаDB.
- расстояние между точкамиDи В3звенаDB.
Линейная скорость точки Е
![]()
Так как
![]() и относительная скорость
и относительная скорость![]() , то направление скорости
, то направление скорости![]() совпадает с направлением скорости
совпадает с направлением скорости![]() ,
а величина
,
а величина![]() найдётся из уравнения
найдётся из уравнения
![]() ,
,
где
![]() - расстояние между точкамиDиEзвена 3.
- расстояние между точкамиDиEзвена 3.
На плане скоростей (рис. 5.7) абсолютная
скорость точки Е изображена вектором
ре. Значение вектора
![]() найдётся
найдётся
![]() .
.
5.4.Определение ускорений точек звеньев и угловых ускорения звеньев. (метод планов).
5.4.1.Группа ассура второго класса первого вида.
Ускорение точек звеньев и угловые ускорения звеньев группы Ассура (рис. 5.8) определяются на основании векторных уравнений связывающих абсолютные aабс, переносные апер и относительные аотн, ускорения
![]() (5.11)
(5.11)
Для рассматриваемого случая из уравнения (5.11) получим
![]() ;
;
![]() .
(5.12)
.
(5.12)
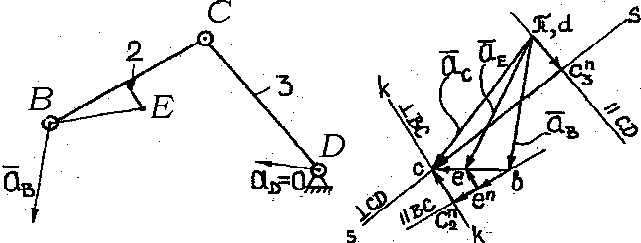
Рис. 5.8 Рис. 5.9
Так как точка С совершает относительно точек B и D неравномерные вращательные относительные движения, уравнения (5.12) запишутся
![]() (5.13)
(5.13)
![]() (5.14)
(5.14)
где
![]() - абсолютное ускорение точки С, которое
необходимоопределить;
- абсолютное ускорение точки С, которое
необходимоопределить;
![]() и
и
![]() - известные как по величине так и по
направлению абсолютные ускорения точек
В иD;
- известные как по величине так и по
направлению абсолютные ускорения точек
В иD;
![]() ,
,
![]() - нормальные
относительные ускорения точки С
относительно точек B
и D;
- нормальные
относительные ускорения точки С
относительно точек B
и D;
![]() ,
,
![]() -
тангенциальные относительные ускорения
точки С относительно точек B
и D.
Положив, что
-
тангенциальные относительные ускорения
точки С относительно точек B
и D.
Положив, что
![]() ,
имеем
,
имеем![]() .
Приравняем правые части уравнений
(5.13) и (5.14).
.
Приравняем правые части уравнений
(5.13) и (5.14).
![]() (5.15)
(5.15)
Значения векторов нормальных
ускорений
![]() ,
,![]() определятся
определятся
![]() ;
;![]()
Вектор ускорения
![]() направлен по звену ВС от точки Ск
точке В.
направлен по звену ВС от точки Ск
точке В.
Вектор ускорения
![]() направлен по звенуDC
от точки С к точке D.
направлен по звенуDC
от точки С к точке D.
Тангенциальные
ускорения
![]() ,
,![]() имеют направление,
перпендикулярное звеньям BC
и DC
соответственно. Таким образом в
уравнении(5.15неизвестны только величины
ускорений
имеют направление,
перпендикулярное звеньям BC
и DC
соответственно. Таким образом в
уравнении(5.15неизвестны только величины
ускорений
![]() и
и![]() ,
определять которые
будем из плана ускорений.
,
определять которые
будем из плана ускорений.
План ускорений (рис. 5.9)строится в масштабе a , величина которого выбирается из удобства вычислений и графических построений.
Масштаб a
определяется аналогично масштабу v.
Размерность масштаба
![]() .
.
Последовательность построения плана ускорений:
1. Выбираем полюс (рис. 5.9).
2. Из полюса
проводим по направлению вектора
![]() отрезок b,
который изображает в масштабе a
величину ускорения
отрезок b,
который изображает в масштабе a
величину ускорения
![]() .
Вектор ускорения
.
Вектор ускорения
![]() остался в полюсе .
остался в полюсе .
3. В соответствии с уравнением
(5.15) из конца вектора b
проводим отрезок bc2n,
параллельный_звену BС
в направлении точки B,
который изображает вектор
![]() ,
а из полюса
проводим отрезок c3n
параллельный звену DC
(в направлении к точке D),
который изображает в масштабе a
, вектор
,
а из полюса
проводим отрезок c3n
параллельный звену DC
(в направлении к точке D),
который изображает в масштабе a
, вектор
![]() .
.
4. В соответствии с уравнением
(5.5) из конца вектора b
проводим отрезок bc2n,
параллельный_звену BС
в направлении точки B,
который изображает вектор
![]() ,
а из полюса
проводим отрезок c3n
параллельный звену DC
(в направлении к точке D),
который изображает в масштабе a
, вектор
,
а из полюса
проводим отрезок c3n
параллельный звену DC
(в направлении к точке D),
который изображает в масштабе a
, вектор
![]() .
.
5. Из точек c2n
и c3n
проводим линии k
- k
и s
- s,
перпендикулярные звеньям СB
и СD.
По этим линиям, k
- k
и s
– s
направлены ускорения
![]() и
и
![]() соответсвенно. Точка
С определит направление векторов: c2nc
- соответствующего ускорению
соответсвенно. Точка
С определит направление векторов: c2nc
- соответствующего ускорению
![]() ,
,![]() - соответствующего ускорению
- соответствующего ускорению![]() ,с
- соответствующего ускорению аС,
которые удовлетворяют векторные
уравнения (2.9) - (2.11). Вектор bс
определяет в масштабе
a
относительное ускорение
,с
- соответствующего ускорению аС,
которые удовлетворяют векторные
уравнения (2.9) - (2.11). Вектор bс
определяет в масштабе
a
относительное ускорение
![]() Вектор c
определяет в масштабе a
ускорение
Вектор c
определяет в масштабе a
ускорение
![]() .
.
Величина абсолютного ускорения точки С найдется
![]()
5.Звенья 2 и 3 совершают
неравномерные вращательные движения
относительно точек В
и D.
Количественно эта неравномерность
вращательного движения определяется
тангенциальными ускорениями
![]() |
и
|
и
![]() ,
которые могут быть выражены через
угловыеускорения звеньев
2 и 3,
,
которые могут быть выражены через
угловыеускорения звеньев
2 и 3,
![]() ;
;
![]() ,
,
Откуда с учетом плана ускорений
![]() ;
;
![]()
6.Ускорение точки Е из уравнения (5.11) определится
![]()
или
![]()
Величины векоторов
![]() и
и![]() вычисляются по выражениям
вычисляются по выражениям
![]() ;
;![]() ,
,
где
![]() - расстояние между точкамиВиЕзвена 2.
- расстояние между точкамиВиЕзвена 2.
Вектор
![]() направлен от точкиЕ
к точке В.
Вектор
направлен от точкиЕ
к точке В.
Вектор
![]() направлен перпендикулярно линииЕВ.
направлен перпендикулярно линииЕВ.
На рис. 5.9 отрезки ben
, ene
, be
и
![]() е
изображают
е
изображают
в масштабе
![]() векторы
векторы![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.
