
- •Министерство аграрной политики украины
- •2. Объем курсового проекта
- •3. Порядок выполнения курсового проекта
- •4.Синтез кинематических схем рычажных (стержневых) механизмов.
- •4.4.Синтез кинематической схемы с качающейся кулисой по коэффициенту δ изменеия скорости хода ползуна.
- •4.5.Синтез кинематитческой схемы кривошипно – ползунного механизма по средней скорости ползуна и частоте вращения кривошипа.
- •5.Кинематическое исследование рычажных механизмов
- •5.1.Общие положения
- •5.2.Опеределение перемещений звеньев и траекторий, описываемых точками звеньев.
- •5.3.3.Группа ассура второго класса, третьего вида.
- •5.4.Определение ускорений точек звеньев и угловых ускорения звеньев. (метод планов).
- •5.4.1.Группа ассура второго класса первого вида.
- •5.4.2.Группа ассура второго класса второго вида.
- •5.4.3.Группа ассура второго класса третьего вида.
- •5.5.Построение кинематических диаграмм
- •5.5.1.Построение диаграммы положений.
- •5.5.2.Построение диаграмм скоростей и ускорений.
- •6.Силовой анализ рычажных механизмов.
- •6.1.Общие положения.
- •6.2.Определение сил тяжести и сил инерции.
- •6.3.Силы полезного сопротивления.
- •6.4.Силы в кинематических парах.
- •6.5.Условия статической определимости кинематических цепей и общий порядок силового расчёта.
- •6.6.Силовой расчёт группы ассура второго класса
- •6.7. Силовой расчёт группы ассура второго класса второго вида.
- •6.8. Силовой расчёт группы ассура второго класса третьего вида.
- •6.9. Силовой расчёт входного звена.
- •7.Исследование кулачкового механизма.
- •7.1.Общие положения.
- •7. 2. Синтез кулачкового механизма
- •Из начальных условий (7.6) следует,
- •7.2.2. Синтез профиля кулачка при равноускоренном
- •7.2.3.Синтез профиля кулачка при синусоидальном законе изменения аналога ускорения толкателя.
- •7.2.4. Синтез профиля кулачка при косинусоидальном законе изменеия аналога ускорения толкателя.
- •7.2.5.Выбор минимального радиуса кулачка.
- •7.2.6.Порядок построения профиля кулачка.
- •7.3.2. Экспериментальное уравновешивание
- •7.3.3.Определение значения уравновешивающей
- •8. Исследование зубчатых передач
- •8.1. Общие положения
- •8.2. Зубчатые передачи с неподвижными осями.
- •8.2.1.Синтез зубчатых передач с неподвижными осями.
- •8.4.Зубчатые передачи с подвижными осями.
- •8.3.1 Синтез планетарных зубчатых передач.
- •Условие соосности.
- •Условие отсутствия подрезания и интерференции зубьев.
- •Условие соседства.
- •Условие сборки.
- •8.3. Определение линейных скоростей точек звеньев у планетарных зубчатых передач.
- •9.Задания на курсовое проектирование.
- •Продолжение таблицы 9.1
- •Приложение 1
- •Список литературы
7.3.2. Экспериментальное уравновешивание
КУЛАЧКА
Профиль кулачка (рис. 7.10) вычерчен
кривыми, которые соответствуют углам
его поворота :
![]() (высотой толкателя в верхнем положении)
– профиль кулачка очерчен другой
окружности радиуса
(высотой толкателя в верхнем положении)
– профиль кулачка очерчен другой
окружности радиуса![]() (опускание толкателя фаза сближения) –
радиус кулачка уменьшается, профиль
кулачка очерчен кривой, которая определена
функцией
(опускание толкателя фаза сближения) –
радиус кулачка уменьшается, профиль
кулачка очерчен кривой, которая определена
функцией![]() ;
;
![]() (высотой толкателя в нижнем положении)
– профиль кулачка очерчен дугой радиусомrmin;
(высотой толкателя в нижнем положении)
– профиль кулачка очерчен дугой радиусомrmin;![]() (подъём толкателя – фаза удаления) –
радиус кулачка увеличивается, профиль
кулачка очерчен кривой, которая описана
функцией
(подъём толкателя – фаза удаления) –
радиус кулачка увеличивается, профиль
кулачка очерчен кривой, которая описана
функцией![]() .
.
Рис. 7.10
Положим, что дисковый кулачок (рис. 7.10)
имеем толщину Н, выполнен из стали, имеет
постоянную плотность по объёму, равною
![]() или
или![]() ,
а диаметр распределительного вала, на
котором установлен кулачёк, равенd.
,
а диаметр распределительного вала, на
котором установлен кулачёк, равенd.
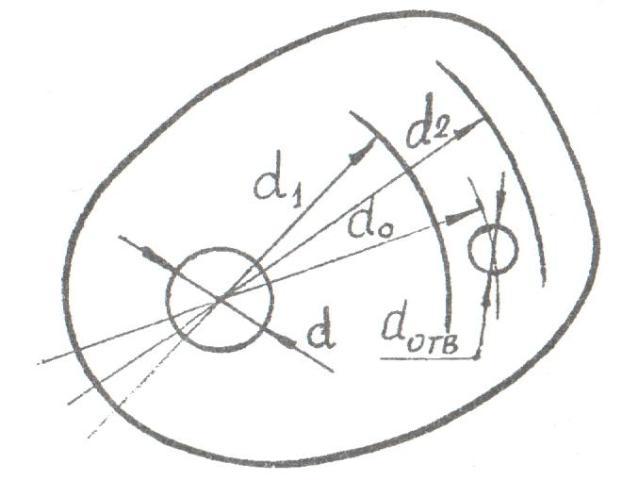
Требуется уравновесить кулачёк, удалив массу с помощью сверления отверстия между окружностями диаметров d1=1,5dиd2=1,5R.
Для этого необходимо определить: 1.положение центра тяжести Тккулачка (рис. 7.11); 2. массуmккулачка; 3. массуm0удаляемого материала для смещения центра тяжести кулачка на ось его вращения. Для этого необходимо:
а)задаться диаметров d0окружности, на которой будет сверлиться отверстие диаметровdотв.
б)определить диаметр dотв. Отверстия из условия равенства массы противовесаmпри массыmоматериала из отверстия, т.е.
mпр= mо
4.Выполнить чертёж кулачка с отверстием диаметров dотв.
Рассмотрим один из способов определения положения центра тяжести кулачка и определения его массы. Разделим кулачёк на четыре части (рис. 7.12). Одна часть І– диск радиусаrminс отверстием в центре диаметровdи трёх частейІІ, ІІІ, ІV, образованных окружностью радиусаrmin и контуром кулачка. ЧастьІІ
соответствует углу
![]() ,
часть ІІІ соответствует углу
,
часть ІІІ соответствует углу![]() ,
часть ІVсоответствует
углу
,
часть ІVсоответствует
углу![]() .
Центр тяжести, (точка Т1) части
кулачкаІрасположен в
точке О, а его масса равна
.
Центр тяжести, (точка Т1) части
кулачкаІрасположен в
точке О, а его масса равна
![]() . (7.44)
. (7.44)
Рис. 7.12
Часть ІІІ имеет вид части кругового кольца. Центр тяжести части кругового кольца с центральным углом φ (рис. 7.13) находится на осиn-nсимметрии, которая делит угол φ пополам , т.е. на биссектрисе этого угла.
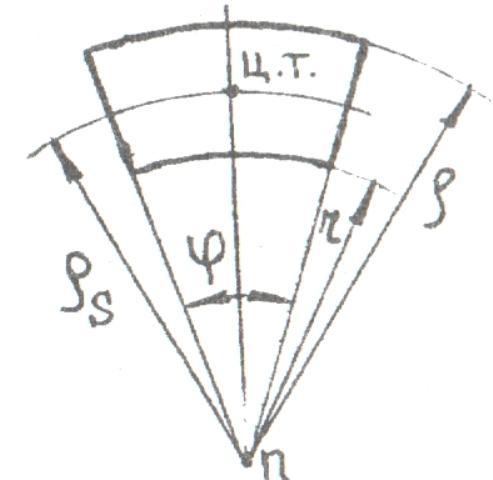
Рис. 7.13.
Координата
![]() центра тяжести (ц.т.) части кругового
кольца определяется из зависимости
центра тяжести (ц.т.) части кругового
кольца определяется из зависимости
![]() ,
(7.45)
угол записан
в радианах(1 радиан
,
(7.45)
угол записан
в радианах(1 радиан
![]() ˚)
˚)
Масса кругового кольца определяется из выражения
![]() ,
(7.46)
,
(7.46)
Где S– площадь кругового кольца.
![]() (мм2)
(мм2)
Окончательно масса части кругового кольца запишется
![]() (7.47)
(7.47)
Часть ІІІ
представляет собой часть кругового
кольца, у которого![]() ,
,
r=rmin, а![]() .
.
Координата центра тяжести (точка Т3частиІІІ кругового кольца из зависимости (7.45) найдётся
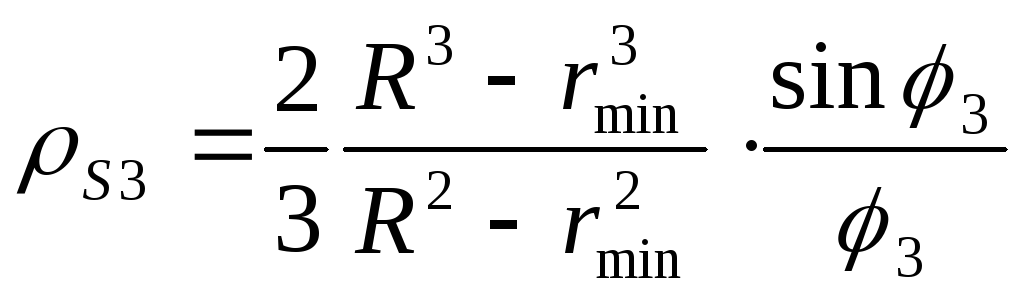 (7.48)
(7.48)
а маса из выражения (7.47)
![]() (7.49)
(7.49)
Опредедление массы и центра тяж ести частей ІІиІVэтих криволинейных треугольниковa0a10c2 и K0K10C4(рис. 7.13) выполним графически.
Построения для криволинейных треугольников a0a10c2 и K0K10C4 будут идентичны, поэтому рассмотрим методику определения центра тяжести и массы для одного из них, например, криволинейного тркцгольникаa0a10c2 (частьІІ кулачка) (рис.7.12).
Известно, что у треугольников центр тяж ести распологается на пересечении медиан (линии соединяющей вершину угла с серединой противоположной стороны). Построим одну из медиан криволинейного треугольника. Для этого отрезок каждого из 10 лучей, с помощью которых строился профиль кулачка между окружностью радиусомrminи профилем кулачка разделим пополам и полученные точки соединим плавной кривой. (криваяa0b2). Далее представим криволинейный треугольникa0a10c2 (рис. 7.14), но со сторонами равными длинами сторон криволинейного треугольникаa0a10c2.
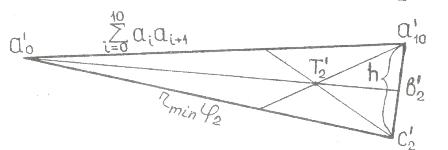
Рис. 7.14
Стороны
треугольника
![]() равны
равны
![]() , (7.50)
, (7.50)
угол
![]() измеряется в радианах:
измеряется в радианах:
![]() ; (7.51)
; (7.51)
длина стороны
![]() подсчитывается как сумма длин хорд
подсчитывается как сумма длин хорд
a0a1 ; a1a2 ; a2a3 ; a3a4 и т.д. (рис. 7.12), т.е.
![]() (7.52)
(7.52)
Центр тяжести треугольника
![]() лежит в точке Т΄2(пересечения
медиан).
лежит в точке Т΄2(пересечения
медиан).
Переносим точку
Т΄2 на кривуюa0b2(рис. 7.12). Для этого измерим отрезок![]() (рис. 7.14), а кривуюa0b2
представим как систему хорд,
соединяющих точки пересечения этой
кривой с лучами Оаi
. На ломанной линииa0b2от точкиb2 отложим
измеренное ранее у треугольника
(рис. 7.14), а кривуюa0b2
представим как систему хорд,
соединяющих точки пересечения этой
кривой с лучами Оаi
. На ломанной линииa0b2от точкиb2 отложим
измеренное ранее у треугольника![]() расстояние
расстояние![]() .
В полученную точку Т*2на
одной из хорд ломанной линииa0b2
проведём луч из точки О.
.
В полученную точку Т*2на
одной из хорд ломанной линииa0b2
проведём луч из точки О.
Пересечение этого луча с кривой a0b2 и определит искомую точку Т2– центр тяжести частиІІ кулачка.
Массу m2частиІІ кулачка определим
как массу треугольника![]() .
.
Известно, что
площадь S![]() треугольника определяется как
треугольника определяется как
![]() ,
(7.53)
,
(7.53)
где
![]() - полупериметр, аa,b,c– длины сторон произвольного треугольника.
- полупериметр, аa,b,c– длины сторон произвольного треугольника.
Используя
уравнение (7.53) для
![]() (частьІІ) имеем
(частьІІ) имеем
![]() , (7.54)
, (7.54)
Где![]() .
.
Используя зависимости (7.46) и (7.54), получим массу m2
![]() . (7.55)
. (7.55)
Аналогичными построениями, как и для части ІІ кулачка, получаем координату Т4 части ІVкулачка, а её масса определится
![]() (7.56)
(7.56)
Таким образом на чертеже (рис. 7.12) имеем точки Т1, Т2 , Т3, Т4 , В которых условно сосредоточены массыm1, m2,m3, m4, соответственно.
Для нахождения центра тяжести кулачка воспользуемся правилом рычага.
Центр тяжести масс m1 иm3точка Т1,3 , находится на линии Т1, Т3и делит отрезок Т1, Т3 обратно пропорционально массамm1 иm3 т.е.
![]() (7.57)
(7.57)
Так как Т1Т1,3=Т1Т3-Т3Т1,3,
то
![]() .
(7.58)
.
(7.58)
В точке Т1,3теперь условно сосредоточена массаm1,3=m1+m3
Центр тяжести масс m2 иm4 , точку Т2,4, находим аналогично предыдущему на линии Т2Т4, а
![]() . (7.59)
. (7.59)
В точке Т2,4теперь условно сосредоточена массаm2,4=m2+m4.
Определим положение центра тяжести кулачка. Соединим точки Т1,3 и Т2,4 прямой. На этой прямой в точке Тклежит центр тяжести кулачка, масса которого
![]() . (7.60)
. (7.60)
Положение точки Ткопределяется как-же по правилу рычага,
![]() . (7.61)
. (7.61)
