
- •Введение
- •Кинематика
- •5. Кинематика вращательного движения.
- •Динамика материальной точки
- •6. Первый закон Ньютона.
- •8. Механические системы.
- •9. Масса.
- •10.Импульс.
- •11.Второй закон Ньютона
- •12.Принцип независимости действия сил.
- •13.Третий закон Ньютона
- •14.Закон сохранения импульса
- •15.Закон движения центра масс.
- •16. Силы в механике.
- •1) Силы тяготения (гравитационные силы).
- •17. Работа, энергия, мощность.
- •18. Кинетическая и потенциальная энергия механической системы
- •19.Закон сохранения энергии.
- •20. Соударения
- •Механика твердого тела
- •21. Момент инерции.
- •22.Кинетическая энергия вращения.
- •23. Момент силы.
- •24.Основное уравнение динамики вращательного движения твердого
- •25. Момент импульса и закон его сохранения.
- •26.Сопоставим основные величины и соотношения для поступательного движения тела и для его вращения вокруг неподвижной оси.
- •Деформации твердого тела
- •27. Деформации твердого тела
- •28. Закон Гука.
- •Элементы механики жидкостей
- •29. Давление в жидкости и газе.
- •30.Уравнение неразрывности.
- •31 .Уравнение Бернулли.
- •32. Вязкость (внутреннее трение)
- •33.Два режима течения жидкостей.
- •34.Методы определения вязкости
- •Потенциальное поле сил.
- •35.Поле сил тяготения.
- •36. Космические скорости.
- •Элементы специальной теории относительности
- •37. Преобразования Галилея
- •38.Постулаты Эйнштейна.
- •39.Преобразования Лоренца.
- •40. Основные соотношения релятивистской динамики.
- •Свободные колебания
- •1. Колебания. Общий подход к изучению колебаний различной физичес кой природы.
- •2. Гармонические колебания и их характеристики.
- •3. Дифференциальное уравнение гармонических колебаний.
- •4. Метод векторных диаграмм.
- •5. Экспоненциальная форма записи гармонических колебаний.
- •6. Механические гармонические колебания.
- •7. Энергия материальной точки, совершающей гармонические колебания.
- •8. Гармонический осциллятор.
- •9. Пружинный маятник.
- •10. Математический маятник.
- •11 .Физический маятник.
- •12.Сложение гармонических колебаний.
- •13. Биения.
- •14. Разложение Фурье.
- •15. Сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты.
- •16.Линейно поляризованные колебания.
- •17. Циркулярно поляризованные колебания.
- •18 .Фигуры Лиссажу.
- •Затухающие и вынужденные колебания
- •19. Затухающие колебания.
- •20.Дифференциальное уравнение свободных затухающих колебаний линейной системы
- •21. Декремент затухания.
- •22.Добротность колебательной системы.
- •Волны в упругой среде.
- •23.Волновой процесс.
- •24.Упругие волны.
- •36. Упругая гармоническая волна.
- •37.Бегущие волны.
- •25.Уравнение плоской волны.
- •25.Фазовая скорость.
- •26. Уравнение сферической волны.
- •28.Принцип суперпозиции.
- •29.Групповая скорость.
- •30. Интерференция волн.
- •31. Стоячие волны.
- •32. Эффект Доплера.
- •2)Приемник приближается к источнику, а источник покоится:
- •3)Источник приближается к приемнику, а приемник покоится:
- •4)Источник и приемник движутся друг относительно друга.
- •1. Статистический и термодинамический методы исследования.
- •2. Термодинамическая система.
- •3. Температура.
- •4. Идеальный газ.
- •5.Закон Бойля-Мариотта.
- •6. Закон Авогадро,
- •7. Закон Дальтона.
- •8 .Закон Гей-Люссака.
- •9. Уравнение состояния идеального газа.
- •10.Основное уравнение молекулярно-кинетической теории идеальных газов.
- •11 .Средняя квадратичная скорость молекул идеального газа:
- •18.Средняя длина свободного пробега молекул.
- •19.Эксперименты, подтверждающие молекулярно-кинетическую теорию.
- •20.Явления переноса.
- •21 .Теплопроводность.
- •22. Диффузия.
- •23.Внутреннее трение (вязкость).
- •24.Внутренняя энергия термодинамической системы.
- •25. Число степеней свободы.
- •26.3Акон Больцмана о равномерном распределении энергии по степеням свободы (закон равнораспределения).
- •27. Первое начало термодинамики.
- •28.Работа газа при его расширении.
- •29. Теплоемкость.
- •30.Молярная теплоемкость при постоянном объеме.
- •31 .Молярная теплоемкость при постоянном давлении. Уравнение Майера.
- •36. Работа газа в адиабатическом процессе.
- •39. Кпд кругового процесса.
- •40. Обратимый и необратимый процессы.
- •41 .Энтропия.
- •42. Изменение энтропии.
- •Изменение энтропии в процессах идеального газа
- •43. Статистическое толкование энтропии.
- •44. Принцип возрастания энтропии.
- •45. Второе начало термодинамики.
- •46.Третье начало термодинамики.
- •47.Тепловые двигатели и холодильные машины.
- •48. Теорема Карно
- •50.Уравнение Ван-дер-Ваальса.
- •51. Изотермы реальных газов.
- •52. Внутренняя энергия реального газа.
- •53.Жидкости и их описание.
- •54. Поверхностное натяжение.
- •55. Смачивание.
- •56. Давление под искривленной поверхностью жидкости.
- •57. Капиллярные явления.
- •58. Кристаллические и аморфные твердые тела.
- •59. Типы кристаллов.
- •60.Дефекты в кристаллах.
- •61 .Теплоемкость твердых тел.
- •62. Изменение агрегатного состояния.
- •63.Фазовые переходы.
- •64.Диаграмма состояния.
- •65.Уравнение Клапейрона-Клаузиуса
- •66.Анализ диаграммы состояния.
- •Приложение
- •6.Вектор.
- •12.Градиент.
- •13.Поток поля через поверхность.
- •14.Производная по объему.
- •15. Дивергенция векторного поля.
- •17.Оператор Лапласа.
- •18.Ротор векторного поля.
- •19.Теорема Стокса.
- •Греческий алфавит
- •Приставки к обозначению единиц
- •Основные физические постоянные
66.Анализ диаграммы состояния.
Диаграмма состояния, позволяет судить, в каком состоянии находится данное вещество при определенных р и Т, а также какие фазовые переходы будут происходить в том или ином процессе.
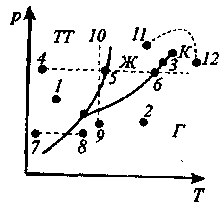 Например,
при
условиях,
обозначенных:
точкой
1 вещество
—
в
твердом
состоянии
(TТ),
2— в
газообразном
(Г).
3—
одновременно
в
жидком
(Ж)
и
газообразном.
Например,
при
условиях,
обозначенных:
точкой
1 вещество
—
в
твердом
состоянии
(TТ),
2— в
газообразном
(Г).
3—
одновременно
в
жидком
(Ж)
и
газообразном.
При изобарном нагреве 4-5-6 в точке 5 начинается плавление, 6— кипение.
При изобарном нагреве 7-8 твердое тело превращается в газ, минуя жидкую фазу.
При изотермическом сжатии 9-10 вещество пройдет три состояния: газ-жидкость-кристалл.
Кривая испарения заканчивается критической точкой (К). Поэтому возможен непрерывный переход вещества из жидкого состояния в газообразное и обратно в обход критической точки, без пересечения кривой испарения (переход 11-12), т.е. такой переход, который не сопровождается фазовыми превращениями.
Это возможно потому, что различие между газом и жидкостью является чисто количественным (оба эти состояния, например, являются изотропными).
Переход же кристаллического состояния в жидкое или газообразное может быть только скачкообразным (в результате фазового перехода), поэтому кривые плавления и сублимации не могут обрываться, как это имеет место для кривой испарения в критической точке.
Кривая плавления уходит в бесконечность, а кривая сублимации идет в точку, где р=0 и Т=0.
Приложение
Основные понятия математического аппарата физики.
1.Понятие производной функции.
Функция
f
называется дифференцируемой
в точке
![]() ,
если существует предел разностного
отношения функцииf
в точке
,
если существует предел разностного
отношения функцииf
в точке
![]()
![]()
Этот
предел называется производной
функции f
в точке
![]() и обозначается:
и обозначается:
![]()
2.Производные некоторых элементарных функций.
|
|
|
|
|
|
|
|
3. Частная производная.
Пусть
функция
f
определена в некоторой окрестности
точки
![]() .
Функцияf
называется дифференцируемой по
.
Функцияf
называется дифференцируемой по
![]() ,
если существует предел разностного
отношения
,
если существует предел разностного
отношения
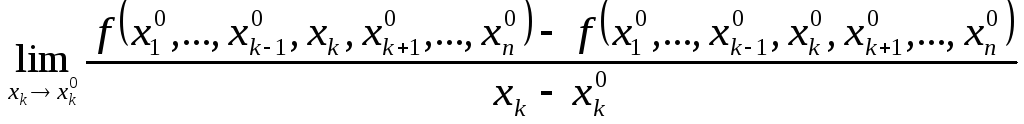
этот
предел называется частной
производной функции
f
(по
![]() )
в точке Р0
и
обозначается:
)
в точке Р0
и
обозначается:
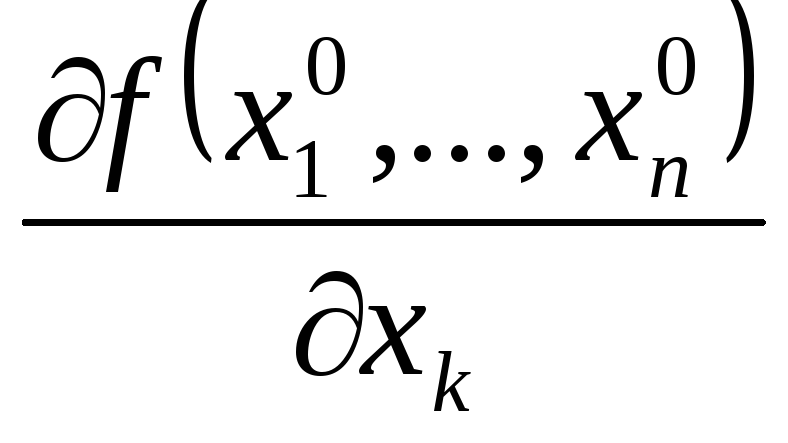 или
или![]()
4.Полный
дифференциал функции
f
в
точке
![]() :
:
![]()
5.Определенный интеграл.
Пусть
функция f(x)
определена и ограничена на отрезке
[a,b].
Разобьем этот отрезок на "элементарные"
отрезки введением и точек
![]() -
следующим образом:
-
следующим образом:![]()
Обозначим
через dx
длину элементарного отрезка
![]() .
В каждом элементарном отрезке выберем
произвольное число
.
В каждом элементарном отрезке выберем
произвольное число
![]() .
.
Число
![]() называется
интегральной
суммой.
называется
интегральной
суммой.
Функция
f(x)
называется интегрируемой на отрезке
[a,b],
если существует число I
со следующим свойством: для любого ε>0
найдется такое δ(ε)>0,
что при любом разбиении на отрезки dx,
для которого dx<δ
, выполняется
неравенствo
![]() независимо от выбора
независимо от выбора![]() .
.
Число
I
называется определенным
интегралом
функции f(x)
на отрезке [а,b]
и обозначается:
![]() .
Здесьх
называется переменной
интегрирования,
a
и b
— соответственно нижним
и верхним пределами интегрирования.
.
Здесьх
называется переменной
интегрирования,
a
и b
— соответственно нижним
и верхним пределами интегрирования.
6.Вектор.
Геометрический
вектор
![]() — это направленный отрезок в пространстве.
Длина вектора
— это направленный отрезок в пространстве.
Длина вектора![]() называется егомодулем
и обозначается:
называется егомодулем
и обозначается:
![]() .
.
В
прямоугольной
декартовой системе
координат
каждый вектор
![]() можно
однозначно представить в виде
можно
однозначно представить в виде
![]() ,где
i,j,k
—
единичные векторы (орты)
по
осям координат x,y,z.
Числа
,где
i,j,k
—
единичные векторы (орты)
по
осям координат x,y,z.
Числа
![]() называютсяпрямоугольными
декартовыми
координатами
вектора
называютсяпрямоугольными
декартовыми
координатами
вектора
![]() .
.
7. Скалярное произведение векторов.
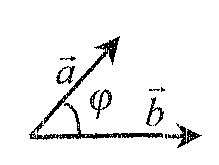
Скалярное
произведение векторов
![]() и
и![]() есть
число
есть
число
![]()
где
φ
- угол между векторами
![]() и
и![]()
8. Векторное произведение векторов.
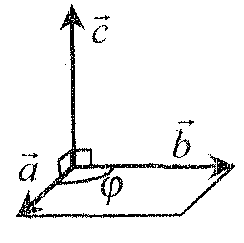
Под
векторным произведением векторов
![]() и
и![]() понимаютвектор
понимаютвектор
![]() ,
имеющий длину
,
имеющий длину![]() (площадь
параллелограмма, построенного на
(площадь
параллелограмма, построенного на
![]() и
и![]() как
на сторонах) и направленный перпендикулярно
к
как
на сторонах) и направленный перпендикулярно
к
![]() и
и![]() ,
причем
так, что векторы
,
причем
так, что векторы
![]() ,
,![]() и
и![]() образуютправую
тройку векторов.
образуютправую
тройку векторов.
Обозначение:
![]() .
.
9.Скалярное поле.
Если
каждой точке М
пространства
ставится в соответствие скалярная
величина U,
то
возникает скалярное
поле
U(M)
(например,
поле температуры неравномерно нагретого
тела, поле плотности в неоднородной
среде, поле электростатического
потенциала). Если М
имеет
декартовы координаты (x,y,z),
то
пишут U
= U(x,y,z)
или
![]() с векторным аргументом (радиусом
вектором)
с векторным аргументом (радиусом
вектором)![]() .
.
10. Векторное поле
Если
каждой точке М
ставится
в соответствие вектор
![]() ,
то говорят овекторном
поле
,
то говорят овекторном
поле
![]() (например,
поле скоростей движущейся жидкости,
гравитационное поле Солнца, поле
электрической напряженности, поле
магнитной напряженности). В декартовых
координатах:
(например,
поле скоростей движущейся жидкости,
гравитационное поле Солнца, поле
электрической напряженности, поле
магнитной напряженности). В декартовых
координатах:
![]()
где
![]() - радиус-вектор. КомпонентыAx,Ay,Az
образуют
три
скалярных поля
и
однозначно определяют
- радиус-вектор. КомпонентыAx,Ay,Az
образуют
три
скалярных поля
и
однозначно определяют
![]() —
векторную функцию векторного аргумента.
—
векторную функцию векторного аргумента.
11.Производная по направлению.
Пусть
скалярное поле
![]() имеет в некоторой точкеМ0
значение U0,
и
пусть при перемещении
имеет в некоторой точкеМ0
значение U0,
и
пусть при перемещении
![]() по направлению вектора
по направлению вектора![]() мы
приходим из точки М0
в
точку М,
где
скалярное поле имеет значение
Us.
Приращение
U
при
этом перемещении равно
мы
приходим из точки М0
в
точку М,
где
скалярное поле имеет значение
Us.
Приращение
U
при
этом перемещении равно
![]() .
Предел отношения этого приращения
dU
к
численной величине перемещения ds
называется
производной
скаляра
U
в
точке
М0
по
направлению
.
Предел отношения этого приращения
dU
к
численной величине перемещения ds
называется
производной
скаляра
U
в
точке
М0
по
направлению
![]() :
:
![]()
Значение
этой производной существенно
зависит
от
выбора направления
![]() и
ее ни в коем случае нельзя
смешивать
с
обыкновенной частной производной по
скалярному параметру s.
Чтобы подчеркнуть это обстоятельство,
часто такую производную обозначают:
и
ее ни в коем случае нельзя
смешивать
с
обыкновенной частной производной по
скалярному параметру s.
Чтобы подчеркнуть это обстоятельство,
часто такую производную обозначают: ![]()
