
- •Методическое пособие
- •Введение
- •Понятие неопределенного интеграла, его свойства. Таблица интегралов. Непосредственное интегрирование
- •Метод введения новой переменной
- •Метод интегрирования по частям.
- •Интегрирование рациональных функций
- •Интегрирование тригонометрических функций
- •Интегрирование иррациональных функций
- •Определенный интеграл как предел интегральных сумм. Геометрический и экономический смысл
- •Свойства определенного интеграла
- •Интеграл с переменным верхним пределом интегрирования. Формула Ньютона-Лейбница
- •Формула Ньютона-Лейбница
- •Вычисление определенных интегралов
- •Несобственные интегралы Несобственные интегралы с бесконечными пределами интегрирования
- •Несобственные интегралы от неограниченных функций
- •Приложения определенного интеграла Геометрические приложения определенного интеграла Вычисление площадей плоских фигур
- •Вычисление длины дуги
- •Нахождение объёма тела по площадям поперечных сечений
- •Вычисление объемов тел вращения
- •Площадь поверхности вращения
- •Приложения определенного интеграла к решению некоторых задач механики и физики
- •Использование понятия определенного интеграла в экономике
- •Приближённое вычисление определённых интегралов
- •Квадратурные формулы левых и правых прямоугольников
- •Квадратурная формула центральных прямоугольников
- •Квадратурная формула трапеций
- •Оценки ошибок формул трапеций и центральных прямоугольников
- •Квадратурная формула Симпсона (формула парабол)
- •Квадратурные формулы более высокого порядка точности
- •Практическая оценка погрешности при применении квадратурных формул
- •Задания для самостоятельного решения
- •9. Найти
- •Набор заданий для выполнения расчетно-графической работы
- •Теоретические упражнения
- •Расчетные задания
- •Формулы. Справочный материал. Неопределенный интеграл
- •Определенный интеграл
- •Несобственные интегралы
- •Литература
Приложения определенного интеграла Геометрические приложения определенного интеграла Вычисление площадей плоских фигур
Пусть
функция y=f(x)
неотрицательна и непрерывна на отрезке
[a,
b].
Тогда по геометрическому смыслу
определенного интеграла площадь S
под кривой y=f(x)
на [ a,
b]
численно равна определенному интегралу
![]() ,
т.е.
,
т.е.
S=![]() .
.
Пример.
Найти площадь фигуры, ограниченной
линиями
![]()
S
=
 (кв. ед.)
(кв. ед.)
Пусть
функция y=f(x)
неположительна и непрерывна на отрезке
[a,
b].
Площадь S
над кривой y=f(x)
на [ a,
b]
отличается знаком от определенного
интеграла
![]() ,
т.е.
,
т.е.
S=
-![]() .
(17)
.
(17)
Приведем формулу, применение которой упрощает решение задач на вычисление площадей плоских фигур.
Теорема.
Пусть на отрезке [a,
b]
заданы непрерывные функции y=f1(x)
и y=f2(x)
такие, что
![]() .
Тогда площадьS
фигуры, заключенной между кривыми
y=f1(x)
и y=f2(x)
на отрезке
[ a,
b]
вычисляется по формуле
.
Тогда площадьS
фигуры, заключенной между кривыми
y=f1(x)
и y=f2(x)
на отрезке
[ a,
b]
вычисляется по формуле
S=![]() .
(18)
.
(18)
Пример.
Вычислить площадь фигуры, ограниченной
линиями
![]()
Найдем
координаты точек пересечения параболы
![]() и прямой
и прямой![]() ,
решив систему этих уравнений: (-1; -1) и
(2; 2). На отрезке [-1; 2]
,
решив систему этих уравнений: (-1; -1) и
(2; 2). На отрезке [-1; 2]
![]() .
Воспользуемся формулой (18), полагая
f2(x)=x,
f1(x)=x2
– 2. Абсциссы
точек пересечения линий зададут пределы
интегрирования:
.
Воспользуемся формулой (18), полагая
f2(x)=x,
f1(x)=x2
– 2. Абсциссы
точек пересечения линий зададут пределы
интегрирования:

П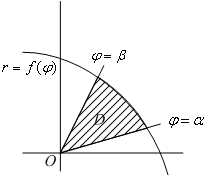 лощадькриволинейного
сектора,
ограниченного кривой, заданной в полярных
координатах уравнением r=f(
лощадькриволинейного
сектора,
ограниченного кривой, заданной в полярных
координатах уравнением r=f(![]() )
и двумя лучами
)
и двумя лучами![]() и
и![]() вычисляется по формуле:
вычисляется по формуле:

Пример.
Найдём площадь
![]() области,
ограниченной частью спиралиr=a
области,
ограниченной частью спиралиr=a![]() (a>0)
при
(a>0)
при
![]() ;
;![]() и
отрезком
и
отрезком![]() ;
;![]() оси
оси![]() (см.
рис.).
(см.
рис.).

Применяя формулу, получаем:

Если область
![]() имеет
границу, состоящую из двух отрезков
лучей
имеет
границу, состоящую из двух отрезков
лучей![]() и
и![]() (эти отрезки могут вырождаться в одну
точку) и двумя линиями, заданными
уравнениями в полярных координатах:r=f1(
(эти отрезки могут вырождаться в одну
точку) и двумя линиями, заданными
уравнениями в полярных координатах:r=f1(![]() )
иr=f2(
)
иr=f2(![]() ),
причёмf1(
),
причёмf1(![]() f2(
f2(![]() ),
при всех
),
при всех![]()
![]() (см.рис.)
(см.рис.)
т о
площадь
о
площадь![]() области
области![]() можно
представить как разность двух площадей:S2—
площади области, лежащей между лучами
можно
представить как разность двух площадей:S2—
площади области, лежащей между лучами
![]() и
и![]() ,
и линиейr=f2(
,
и линиейr=f2(![]() ),
иS1—
площади области, лежащей между лучами
),
иS1—
площади области, лежащей между лучами
![]() и
и![]() ,
линиейr=f1(
,
линиейr=f1(![]() ).
).
Каждую из площадей S1 и S2 можно подсчитать по формуле, так что получаем в итоге

Если кривая задана параметрическими уравнениями x=x=(t) и y=y(t), то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x=a, x=b и отрезком [a,b] оси Ox выражается формулой
 .
.
Вычисление длины дуги
1.
Явное задание кривой.
В этом случае кривая задается в виде
![]() ,
,![]() ,
и длина ее дуги равна L=
,
и длина ее дуги равна L= .
.
2. Кривая
в полярных координатах.
Уравнение
кривой имеет в этом случае вид
![]() и длина ее дуги равнаL=
и длина ее дуги равнаL=![]() .
.
3.
Параметрическое
задании кривой.
Пусть функции
x(t)
и y(t)
имеют на отрезке
![]() непрерывные
производные
непрерывные
производные
![]() и
и![]() .
Тогда длина дуги кривой
.
Тогда длина дуги кривой
L= .
.
Пример.
Найдём длину дуги кривой (циклоиды),
заданной на плоскости
![]() параметрическими
уравнениями
параметрическими
уравнениями
![]()
л ежащей
между точкамиO(0;0)
(соответствует
ежащей
между точкамиO(0;0)
(соответствует
![]() )
иA(2
)
иA(2![]() a;0)
(соответствует
a;0)
(соответствует
![]() ).
).
Для функций
f1(t)=a(t-sint)
и f2(t)=a(1-cost)
вычислим производные:
![]()
Тогда искомая длина дуги равна

П ример.
Пусть линия на плоскости с полярными
координатами (r;
ример.
Пусть линия на плоскости с полярными
координатами (r;![]() )
задана уравнениемr=a
)
задана уравнениемr=a![]() (a>0).
Поскольку функция f(
(a>0).
Поскольку функция f(![]() )=a
)=a![]() периодична
с периодом
периодична
с периодом
![]() ,
достаточно рассматривать только значения
аргумента
,
достаточно рассматривать только значения
аргумента![]()
![]() ,
при которых выражение
,
при которых выражение![]() неотрицательно.
Кривая имеет вид, изображённый на
следующем рисунке.
неотрицательно.
Кривая имеет вид, изображённый на
следующем рисунке.
Найдём длину этой линии.
Имеем

Поэтому искомая
длина
![]() равна
равна


