
- •Методическое пособие
- •Введение
- •Понятие неопределенного интеграла, его свойства. Таблица интегралов. Непосредственное интегрирование
- •Метод введения новой переменной
- •Метод интегрирования по частям.
- •Интегрирование рациональных функций
- •Интегрирование тригонометрических функций
- •Интегрирование иррациональных функций
- •Определенный интеграл как предел интегральных сумм. Геометрический и экономический смысл
- •Свойства определенного интеграла
- •Интеграл с переменным верхним пределом интегрирования. Формула Ньютона-Лейбница
- •Формула Ньютона-Лейбница
- •Вычисление определенных интегралов
- •Несобственные интегралы Несобственные интегралы с бесконечными пределами интегрирования
- •Несобственные интегралы от неограниченных функций
- •Приложения определенного интеграла Геометрические приложения определенного интеграла Вычисление площадей плоских фигур
- •Вычисление длины дуги
- •Нахождение объёма тела по площадям поперечных сечений
- •Вычисление объемов тел вращения
- •Площадь поверхности вращения
- •Приложения определенного интеграла к решению некоторых задач механики и физики
- •Использование понятия определенного интеграла в экономике
- •Приближённое вычисление определённых интегралов
- •Квадратурные формулы левых и правых прямоугольников
- •Квадратурная формула центральных прямоугольников
- •Квадратурная формула трапеций
- •Оценки ошибок формул трапеций и центральных прямоугольников
- •Квадратурная формула Симпсона (формула парабол)
- •Квадратурные формулы более высокого порядка точности
- •Практическая оценка погрешности при применении квадратурных формул
- •Задания для самостоятельного решения
- •9. Найти
- •Набор заданий для выполнения расчетно-графической работы
- •Теоретические упражнения
- •Расчетные задания
- •Формулы. Справочный материал. Неопределенный интеграл
- •Определенный интеграл
- •Несобственные интегралы
- •Литература
Квадратурная формула центральных прямоугольников
Снова рассмотрим
отрезки разбиения
![]()
![]() ,
гдеi=1,2…n.
и x0=a
и xn=b
, выберем в качестве точек разметки
середины каждого из этих отрезков, то
есть точки
,
гдеi=1,2…n.
и x0=a
и xn=b
, выберем в качестве точек разметки
середины каждого из этих отрезков, то
есть точки

(Мы будем эти середины обозначатьxi-1/2.) Возьмём за приближённое значение интеграла интегральную сумму, построенную по такому размеченному разбиению. Каждое слагаемое в этой сумме, равное
![]()
выражает
площадь прямоугольника с основанием
![]()
![]() ,и
высотой, равной значению функции в
середине этого отрезка (см. рис.3):
,и
высотой, равной значению функции в
середине этого отрезка (см. рис.3):

Рис.3.
Получим тогда квадратурную формулу:

называемую формулой центральных прямоугольников.
Если
взять все отрезки разбиения равной
длины
![]() ,
то эта квадратурная формула принимает
вид
,
то эта квадратурная формула принимает
вид

Заметим, что в этом
случае
![]()
Для выяснения
характера ошибки
![]() ,
возникающей при замене
,
возникающей при замене![]() наIR,
заметим, что если функция f(x)
дифференцируема, то прямоугольник
площади S
наIR,
заметим, что если функция f(x)
дифференцируема, то прямоугольник
площади S![]() равновелик
трапеции, верхней стороной которой
служит касательная к графику y=
f(x),
проведённая при
равновелик
трапеции, верхней стороной которой
служит касательная к графику y=
f(x),
проведённая при
![]() (см.
рис.4):
(см.
рис.4):

Рис.4.
Действительно,
заштрихованные на рисунке треугольники
равны, отчего равны площади прямоугольника
![]() и
трапеции
и
трапеции![]() .
.
Отсюда следует,
что если функция f(x)
имеет вторую производную, то при
![]() график
является выпуклым кверху иIR>I
(так как из чертежа видно, что площадь
трапеции, равная Si,
больше площади под графиком функции, а
при график является выпуклым книзу и
IR<I.
Значит, при
график
является выпуклым кверху иIR>I
(так как из чертежа видно, что площадь
трапеции, равная Si,
больше площади под графиком функции, а
при график является выпуклым книзу и
IR<I.
Значит, при
![]() на
на
![]() .
.![]() получаем
получаем![]() ,
а при
,
а при![]() —
—![]() .
.
Квадратурная формула трапеций
Пусть снова взято
разбиение отрезка
![]() .
.![]() на части
на части![]()
![]() ,
где i=1,2…n. Приближённо заменим площадь
под графиком y=f(x), лежащую над промежутком
разбиения
,
где i=1,2…n. Приближённо заменим площадь
под графиком y=f(x), лежащую над промежутком
разбиения![]()
![]() ,
на площадь трапеции, параллельными
основаниями которой служат отрезки,
задающие значения функции в концах
промежутка, то есть f(xi-1)и f(xi) (см. рис.5).
,
на площадь трапеции, параллельными
основаниями которой служат отрезки,
задающие значения функции в концах
промежутка, то есть f(xi-1)и f(xi) (см. рис.5).
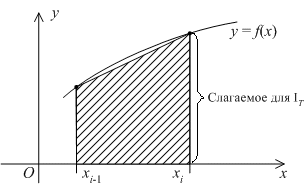
Рис.5.
Тогда площадь такой трапеции равна, очевидно,

Суммируя все площади Si, получаем квадратурную формулу трапеций:

Это та же формула, что была получена при комбинировании формул левых и правых прямоугольников, в которой мы обозначали правую часть через Irl.
Заметим, что при
подсчёте площади каждой очередной
трапеции Si
достаточно вычислить значение функции
f
лишь в одной новой точке — в правом
конце xi
очередного
промежутка
![]()
![]() ,
поскольку точкаxi-1
была правым
концом предыдущего отрезка и значение
в этой точке уже было вычислено при
нахождении площади предыдущей трапеции.
,
поскольку точкаxi-1
была правым
концом предыдущего отрезка и значение
в этой точке уже было вычислено при
нахождении площади предыдущей трапеции.
Если все отрезки
разбиения выбираются одинаковой длины
![]() ,
то формула трапеций приобретает вид
,
то формула трапеций приобретает вид
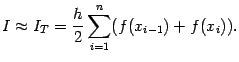
Все значения функции f(xi), кроме f(x0)=f(a) иf(xn)=f(b), встречаются в этой формуле по два раза. Поэтому, объединяя равные слагаемые, мы можем записать формулу трапеций в виде

где xi=a+ih , i=1,…,n-1.
Пусть функция f(x)
имеет вторую производную f//(x),
сохраняющую знак на интервале (a;b).
Как легко видно из предыдущего рисунка,
характер ошибки
![]() этой квадратурной формулы таков: еслиf//(x)<0,
то есть если график y=f(x)
является выпуклым кверху, то I>IT,
значит,
этой квадратурной формулы таков: еслиf//(x)<0,
то есть если график y=f(x)
является выпуклым кверху, то I>IT,
значит,
![]() ;
если жеf//(x)>0
и график имеет выпуклость книзу, то I<IT
и
;
если жеf//(x)>0
и график имеет выпуклость книзу, то I<IT
и
![]() .
.
Если сравнить это с изученными выше
значениями ошибки
![]() формулы
центральных прямоугольников, то мы
видим, что для функций, вторая производная
которых сохраняет знак на отрезке
интегрирования, знаки ошибок
формулы
центральных прямоугольников, то мы
видим, что для функций, вторая производная
которых сохраняет знак на отрезке
интегрирования, знаки ошибок![]() и
и![]() противоположны. Возникает желание
соединить формулу трапеций и формулу
центральных прямоугольников так, чтобы
эти ошибки по возможности скомпенсировались.
Для того, чтобы понять, какую комбинацию
формул следует брать, нам нужно выяснить,
какую величину имеют эти ошибки
противоположны. Возникает желание
соединить формулу трапеций и формулу
центральных прямоугольников так, чтобы
эти ошибки по возможности скомпенсировались.
Для того, чтобы понять, какую комбинацию
формул следует брать, нам нужно выяснить,
какую величину имеют эти ошибки![]() и
и![]() в зависимости от выборашага
в зависимости от выборашага![]() .
Эти оценкиошибок
имеют и самостоятельное значение,
поскольку позволяют узнать точность
полученного при применении соответствующей
квадратурной формулы приближённого
значения интеграла.
.
Эти оценкиошибок
имеют и самостоятельное значение,
поскольку позволяют узнать точность
полученного при применении соответствующей
квадратурной формулы приближённого
значения интеграла.
