
- •Методическое пособие
- •Введение
- •Понятие неопределенного интеграла, его свойства. Таблица интегралов. Непосредственное интегрирование
- •Метод введения новой переменной
- •Метод интегрирования по частям.
- •Интегрирование рациональных функций
- •Интегрирование тригонометрических функций
- •Интегрирование иррациональных функций
- •Определенный интеграл как предел интегральных сумм. Геометрический и экономический смысл
- •Свойства определенного интеграла
- •Интеграл с переменным верхним пределом интегрирования. Формула Ньютона-Лейбница
- •Формула Ньютона-Лейбница
- •Вычисление определенных интегралов
- •Несобственные интегралы Несобственные интегралы с бесконечными пределами интегрирования
- •Несобственные интегралы от неограниченных функций
- •Приложения определенного интеграла Геометрические приложения определенного интеграла Вычисление площадей плоских фигур
- •Вычисление длины дуги
- •Нахождение объёма тела по площадям поперечных сечений
- •Вычисление объемов тел вращения
- •Площадь поверхности вращения
- •Приложения определенного интеграла к решению некоторых задач механики и физики
- •Использование понятия определенного интеграла в экономике
- •Приближённое вычисление определённых интегралов
- •Квадратурные формулы левых и правых прямоугольников
- •Квадратурная формула центральных прямоугольников
- •Квадратурная формула трапеций
- •Оценки ошибок формул трапеций и центральных прямоугольников
- •Квадратурная формула Симпсона (формула парабол)
- •Квадратурные формулы более высокого порядка точности
- •Практическая оценка погрешности при применении квадратурных формул
- •Задания для самостоятельного решения
- •9. Найти
- •Набор заданий для выполнения расчетно-графической работы
- •Теоретические упражнения
- •Расчетные задания
- •Формулы. Справочный материал. Неопределенный интеграл
- •Определенный интеграл
- •Несобственные интегралы
- •Литература
Приближённое вычисление определённых интегралов
Рассмотрим задачу о приближённом нахождении значения определённого интеграла
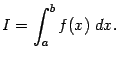
Относительно
подынтегральной функции f(x)
мы будем предполагать, что она непрерывна
на отрезке интегрирования, а также,
когда это понадобится, что она имеет на
этом отрезке производные до некоторого
порядка. Вычислять значение интеграла
![]() мы
будем по значениям функцииf(x)
в некоторых точках отрезка xi.
Эти значения yi=f(xi.)
мы будем предполагать известными, то
есть предполагать, что у нас есть
некоторый эффективный способ вычисления
значений функции с любой требуемой
точностью. Формулы, позволяющие по
известным значениям yi
приближённо
определить значение
мы
будем по значениям функцииf(x)
в некоторых точках отрезка xi.
Эти значения yi=f(xi.)
мы будем предполагать известными, то
есть предполагать, что у нас есть
некоторый эффективный способ вычисления
значений функции с любой требуемой
точностью. Формулы, позволяющие по
известным значениям yi
приближённо
определить значение
![]() ,
называютсяквадратурными
формулами.
,
называютсяквадратурными
формулами.
Для наглядности
мы будем прибегать к геометрической
интерпретации смысла определённого
интеграла, как площади некоторой
криволинейной трапеции, в случае функции
f(x)![]() .
Следует, однако, иметь в виду, что
квадратурные формулы, которые мы будем
получать, имеют смысл для функций,
принимающих значения произвольного
знака.
.
Следует, однако, иметь в виду, что
квадратурные формулы, которые мы будем
получать, имеют смысл для функций,
принимающих значения произвольного
знака.
При f(x)![]() вычислить интеграл
вычислить интеграл![]() значит
найти площадь под графикомy=f(x),
расположенную над отрезком
значит
найти площадь под графикомy=f(x),
расположенную над отрезком
![]() .
.![]() .
Естественной идеей является следующее
построение: разобьём отрезок на части
точками деленияx1,
x2,
… xn-1
и положим
x0=a
и xn=b
(см. определение значения определённого
интеграла). Тогда разбиение отрезка
.
Естественной идеей является следующее
построение: разобьём отрезок на части
точками деленияx1,
x2,
… xn-1
и положим
x0=a
и xn=b
(см. определение значения определённого
интеграла). Тогда разбиение отрезка
![]() .
.![]() состоит из отрезков
состоит из отрезков![]()
![]() приi=1,2…n.
Вместо площади под графиком, равной
приi=1,2…n.
Вместо площади под графиком, равной
![]() ,
будем приближённо находить суммарную
площадь узких полосок, лежащих над
отрезками разбиения
,
будем приближённо находить суммарную
площадь узких полосок, лежащих над
отрезками разбиения![]()
![]() (см. рис.1).
(см. рис.1).
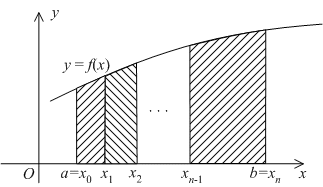
Рис.1.
Квадратурные формулы левых и правых прямоугольников
Самый простой
метод приближённого вычисления площадей
узких полосок — заменить их площадями
Si
прямоугольников,
основанием которых служит отрезок
![]()
![]() на оси
на оси![]() ,
а высотой — отрезок, задающий значение
функции в одном из концов основания, то
есть либо в точкеxi-1,
либо в точке xi.
Тогда в первом случае площадь Si
равняется f(xi-1)(
xi-
xi-1),
а во втором
,
а высотой — отрезок, задающий значение
функции в одном из концов основания, то
есть либо в точкеxi-1,
либо в точке xi.
Тогда в первом случае площадь Si
равняется f(xi-1)(
xi-
xi-1),
а во втором
Si= f(xi)( xi- xi-1).
Суммируя
по всем отрезкам разбиения, то есть по
![]() от
от![]() до
до![]() ,
получаем в первом случаеквадратурную
формулу левых прямоугольников:
,
получаем в первом случаеквадратурную
формулу левых прямоугольников:

а во втором случае квадратурную формулу левых прямоугольников:

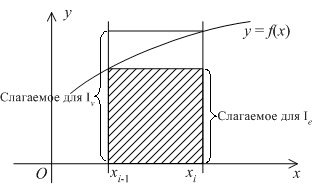
Рис.2.
Из приведённого
чертежа ясно, что ошибки![]() и
и![]() ,
которые возникают при замене точного
значения интеграла
,
которые возникают при замене точного
значения интеграла![]() на
его приближённое значениеIl
или Ir
соответственно, обладают такими
свойствами:
на
его приближённое значениеIl
или Ir
соответственно, обладают такими
свойствами:
если
функция f(x)
возрастает на
![]() .
.![]() ,
то
,
то![]() ,
посколькуI>Il;
,
посколькуI>Il;
если
функция f(x)
убывает на
![]() .
.![]() ,
то
,
то![]() ,
посколькуI<Il;
,
посколькуI<Il;
если
функция f(x)
возрастает на
![]() .
.![]() ,
то
,
то![]() ,
посколькуI<Ir
;
,
посколькуI<Ir
;
если
функция f(x)
убывает на
![]() .
.![]() ,
то
,
то![]() ,
посколькуI>Ir.
,
посколькуI>Ir.
Таким
образом, в случае монотонной функции f
ошибки
![]() и
и![]() имеют
разные знаки. Возникает желание взаимно
скомпенсировать эти ошибки (хотя бы
частично), взяв полусумму чиселIl
и Ir
за приближённое значение интеграла.
Получаем при этом такую квадратурную
формулу:
имеют
разные знаки. Возникает желание взаимно
скомпенсировать эти ошибки (хотя бы
частично), взяв полусумму чиселIl
и Ir
за приближённое значение интеграла.
Получаем при этом такую квадратурную
формулу:

Как мы впоследствии
увидим, полученная квадратурная формула
в точности совпадает с формулой
трапеций.
Она часто применяется на практике для
вычисления интеграла благодаря своей
простоте. Сами же формулы для Il
и Ir
, из которых она возникла, на практике
применяются чрезвычайно редко ввиду
своей малой точности: ошибки
![]() и
и![]() слишком значительны даже при достаточно
мелких разбиениях. Большую точность
обеспечивает следующий метод, применение
которого ничуть не сложнее.
слишком значительны даже при достаточно
мелких разбиениях. Большую точность
обеспечивает следующий метод, применение
которого ничуть не сложнее.
