Нахождение объёма тела по площадям поперечных сечений

Пусть в пространстве задано тело. Пусть построены его сечения плоскостями, перпендикулярными осии проходящими через точкиx на ней. Площадь фигуры, образующейся в сечении, зависит от точки х, определяющей плоскость сечения. Пусть эта зависимость известна и задана непрерывной на функцией. Тогда объем части тела, находящейся между плоскостямих=а и х=в вычисляется по формуле

Пример. Найдём объём ограниченного тела, заключённого между поверхностью цилиндра радиуса :, горизонтальной плоскостьюи наклонной плоскостьюz=2y и лежащего выше горизонтальной плоскости .

Очевидно, что рассматриваемое тело проектируется на осьв отрезок, а приxпоперечное сечение тела представляет собою прямоугольный треугольник с катетамиy и z=2y, где y можно выразить через x из уравнения цилиндра:

Поэтому площадь S(x) поперечного сечения такова:

Применяя формулу, находим объём тела :

Вычисление объемов тел вращения

Пусть на отрезке [a, b] задана непрерывная знакопостоянная функция y=f(x). Объемы тела вращения, образованного вращением вокруг оси Ох (или оси Оу) криволинейной трапеции, ограниченной кривой y=f(x) (f(x)0) и прямыми у=0, х=а, х=b, вычисляются соответственно по формулам:

, (19)

(20)

Если тело образуется при вращении вокруг оси Оу криволинейной трапеции, ограниченной кривойи прямымиx=0, y=c, y=d, то объем тела вращения равен

. (21)

Пример. Вычислить объем тела, полученного вращением фигуры, ограниченной линиями вокруг осиОх.

По формуле (19) искомый объем

(ед.²)

Пример. Пусть в плоскости xOy рассматривается линия y=cosx на отрезке .

Эта линия вращается в пространстве вокруг оси, и полученная поверхность вращения ограничивает некоторое тело вращения (см. рис.). Найдём объёмэтого тела вращения.

Согласно формуле, получаем:

Площадь поверхности вращения

Если дуга кривой, заданная неотрицательной функцией ,, вращается вокруг осиOx, то площадь поверхности вращения вычисляется по формуле , гдеa и b — абсциссы начала и конца дуги.

Если дуга кривой, заданная неотрицательной функцией ,, вращается вокруг осиOy, то площадь поверхности вращения вычисляется по формуле

,

где с и d — абсциссы начала и конца дуги.

Если дуга кривой задана параметрическими уравнениями ,, причем, то

Если дуга задана в полярных координатах , то

.

Пример. Вычислим площадь поверхности, образованной вращением в пространстве вокруг оси части линииy=, расположенной над отрезкомоси.

Так как , то формула даёт нам интеграл

Сделаем в последнем интеграле замену t=x+(1/2) и получим:

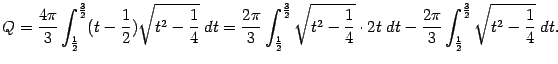
В первом из интегралов правой части сделаем замену z=t²-:

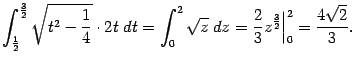
Для вычисления второго из интегралов в правой части обозначим его и проинтегрируем по частям, получив уравнение для:

Перенося в левую часть и деля на 2, получаем

откуда, наконец,

Приложения определенного интеграла к решению некоторых задач механики и физики

Работа переменной силы. Рассмотрим движение материальной точки вдоль оси OX под действием переменной силы f , зависящей от положения точки x на оси, т.e. силы, являющейся функцией x. Тогда работа A, необходимая для перемещения материальной точки из позиции x = a в позицию x = b вычисляется по формуле:

Для вычисления силы давления жидкости используют закон Паскаля, согласно которому давление жидкости на площадку равно ее площади S, умноженной на глубину погружения h, на плотность ρ и ускорение силы тяжести g, т.е.

.

1. Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y=f(x), a≤x≤b, и имеет плотность , тостатические моменты этой дуги M_x и M_y относительно координатных осей Ox и Oy равны

;

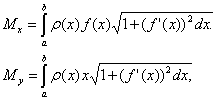моменты инерции I_Х и I_у относительно тех же осей Ох и Оу вычисляются по формулам

а координаты центра масс и— по формулам

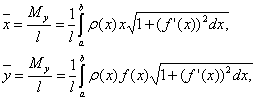
где l— масса дуги, т. е.

Пример 1. Найти статические моменты и моменты инерции относительно осей Ох и Оу дуги цепной линии y=chx при 0≤x≤1.

Если плотность не указана, предполагается, что кривая однородна и . Имеем:Следовательно,

Пример 2. Найти координаты центра масс дуги окружности x=acost, y=asint, расположенной в первой четверти. Имеем:

Отсюда получаем:

В приложениях часто оказывается полезной следующая Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.

Пример 3. Найти координаты центра масс полуокружности

Вследствие симметрии . При вращении полуокружности вокруг оси Ох получается сфера, площадь поверхности которой равна, а длина полуокружности равна па. По теореме Гульдена имеем 4

Отсюда , т.е. центр масс C имеет координаты C.

2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах .

Пример 4. Скорость прямолинейного движения тела выражается формулой (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

Так как путь, пройденный телом со скоростью v(t) за отрезок времени [t₁,t₂], выражается интегралом

то имеем:

П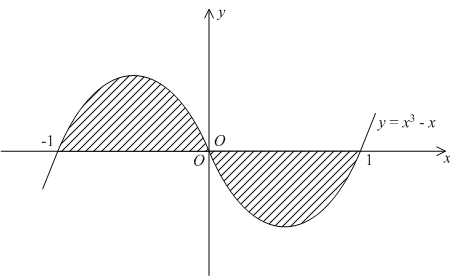ример.  Найдём площадь ограниченной области, лежащей между осьюи линиейy=x³-x. Поскольку

линия пересекает ось в трёх точка:x₁=-1, x₂=0, x₃=1.

Ограниченная область между линией и осью проектируется на отрезок,причём на отрезке,линияy=x³-x идёт выше оси (то есть линииy=0, а на - ниже. Поэтому площадь области можно подсчитать так:

Пример. Найдём площадь области, заключённой между первым и вторым витком спирали Архимедаr=a (a>0) и отрезком горизонтальной оси .

Первый виток спирали соответствует изменению угла в пределах от 0 до, а второй — отдо. Чтобы привести изменение аргументак одному промежутку, запишем уравнение второго витка спирали в виде, . Тогда площадь можно будет найти по формуле, положиви :

Пример. Найдём объём тела, ограниченного поверхностью вращения линииy=4x-x² вокруг оси (при).

Для вычисления объёма тела вращения применим формулу

Имеем:

Пример. Вычислим длину дуги линииy=lncosx, расположенной между прямыми и.

Так как

и

(мы взяли в качестве значения корня , а не -cosx, поскольку cosx >0 при , длина дуги равна

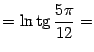
Ответ: .

Пример. Вычислим площадь Q поверхности вращения, полученной при вращении дуги циклоиды x=t-sint ; y=1-cost, при , вокруг оси.

Для вычисления применим формулу:

Имеем: , так что

Для перехода под знаком интеграла к переменной заметим, что приполучаем, а также

Кроме того, предварительно вычислим

(так что) и

Получаем:

Делая замену , приходим к интегралу