9. Вычислить абсолютную линейную невязку полигона:

В нашем примере:

10. Вычислить относительную линейную невязку полигона: m=, где Р - периметр полигона, если , то невязки допустимы и их распределяют пропорционально длинам сторон с противоположными знаками и вычисляют исправленные приращения. Контроль:- сумма исправленных (увязанных) приращений равна нулю.

В нашем примере: m=

Невязка допустима.

11. Вычислить координаты точек по формулам. Контроль — повторное вычисление координат точки 1:

Пример (гр. 11): Х₁=Х₆ + Х₆=55,32 + 394,68 = 450,00 м

У₁ = У₆ + У₆ = — 81,96 + 381,96 = 300,00 м.

Если m=, т. е. относительная линейная невязка недопустима, то необходимо проверить все вычисления, начиная с выписки исходных данных и найти ошибку. Довольно часто ошибаются при вычислении приращений из-за невнимательности: неверно переводят дирекционные углы в румбы, неверно определяют знаки приращений координат (±), вместо cos r берут по таблицам sin r при вычислении ∆Х и∆Уи наоборот. При отыскании подобного рода ошибок следует воспользоваться номограммой на рис. 1.

Из рис 1а видно, что приращения по оси X вверх (к северу) от начала координат возрастают (знак плюс в I и IV четвертях, т. е. при румбах СВ и СЗ), а вниз (к югу) - убывают (знак минус во II и III четвертях, т.е. при румбах ЮВ и ЮЗ); по оси У - возрастание к востоку, убывание - к западу.

По номограмме 1б можно быстро определить грубые промахи в определении абсолютных значений приращений. Для этого циркулем-измерителем откладывают расстояния в масштабе номограммы (взяв его по любой из осей) от начала координат по заданному румбу, спроецировав, полученную точку М на оси координат читают ∆Х и∆У.

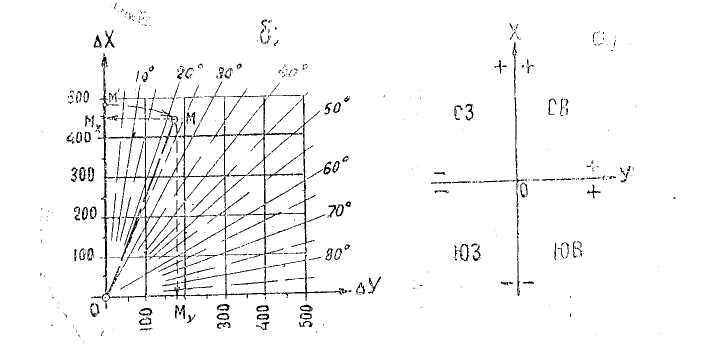
Рис. 1. а) Зависимость знаков приращений координат от румбов.

б) Номограмма для определения грубых просчетов в

вычисленных приращениях координат.

Пример: d= 169,84 м, r = 22⁰22′. Надо найти ∆Х и∆У.

По оси ∆Х циркулем берем ОМ = d =470 м и откладываем его по румбу r = 22,5°, получаем точку М, в точках М_х и М_у берем отсчеты ∆Х = 440м, ∆У = 175 м. Такой точности достаточно для того, чтобы определить порядок величины ошибки и уже потом пересчитать точно (по таблицам и др.).

12. Составить план по координатам. Необходимы линейка, циркуль -измеритель, поперечный масштаб, остро очинённый карандаш твердости 2Т-3Т чтобы обеспечить необходимую графическую точность 0,2 мм, форматный лист чертежной бумаги (ф. А3).

Построить координатную сетку со стороной квадрата 10 см (рис. 2). Сначала через весь формат листа провести две диагонали (АВ и CD), наколоть точку их пересечения (Е) и от нее отложить на диагоналях циркулем-измерителем равные отрезки (АЕ = BE = СЕ = DE) по 14-16 см, последовательно соединить точки А, С, В, D - в результате получится прямоугольник. Параллельные стороны прямоугольника не должны отличаться друг от друга более чем на 0,2 мм. Прямоугольник ACBD разбить на квадраты со стороной 10 см (500 м в масштабе 1 : 5000), для чего на сторонах прямоугольника АС и ВД, а также СВ и AD попарно отложить по 10 см, идентичные точки соединить - получится сетка квадратов. Квадраты проконтролировать - диагонали их должны быть равны, а также отрезки а=а¹, b=b¹.

Сообразно с вычисленными координатами вершин полигона, выбрать начало координат и оцифровать координатную сетку с таким расчетом, чтобы все точки уместились на плане.

Нанести точки полигона по координатам пользуясь поперечным масштабом. Для этого сначала надо по координатам определить квадрат, на который падает данная точка. Отложить на его соответствующих сторонах попарно координаты Х и У (учитывая знаки), идентичные точки соединить, в пересечении наколоть и обвести точку кружком диаметром 2мм. Правильность наноски проверяют откладыванием на соответствующих сторонах квадрата дополнений координат до 500м, т. е. ∆Х = 500-Х; ∆У =500-У или по расстояниям между соседними точками, взятым из ведомости вычислений. Допустимое расхождение - в пределах графической точности.

После проверки все точки соединить прямыми линиями.

Примеры (рис. 2):

1. Нанести точку № 1 по координатам X₁ = +450м, У₁ = +300м. Находим квадрат и откладываем на его сторонах попарно Х₁ = 450м и У₁ = 300м. Правильность нанесения точки проверяем, взяв дополнения ∆Х = 500-450 = 50м, ∆У = 500-300 = 200м и отложив их на соответствующих сторонах квадрата.

2. Нанести точку № 3 по координатам Х₃ = -216,49м, У₃ = +823,16м. Координаты округляем в пределах точности масштаба (до 0,5м) Х₃ = -216,5м, У₃ = 823м. Определяем квадрат. С учетом знаков откладываем Х₃ = -216,5м, от нулевой линии, У₃ = 823-500 = 323м от линии, оцифрованной -500м.

Контроль-дополнения: ∆Х = 500-216,5 = 283,5м, ∆У = 500-323=177м.

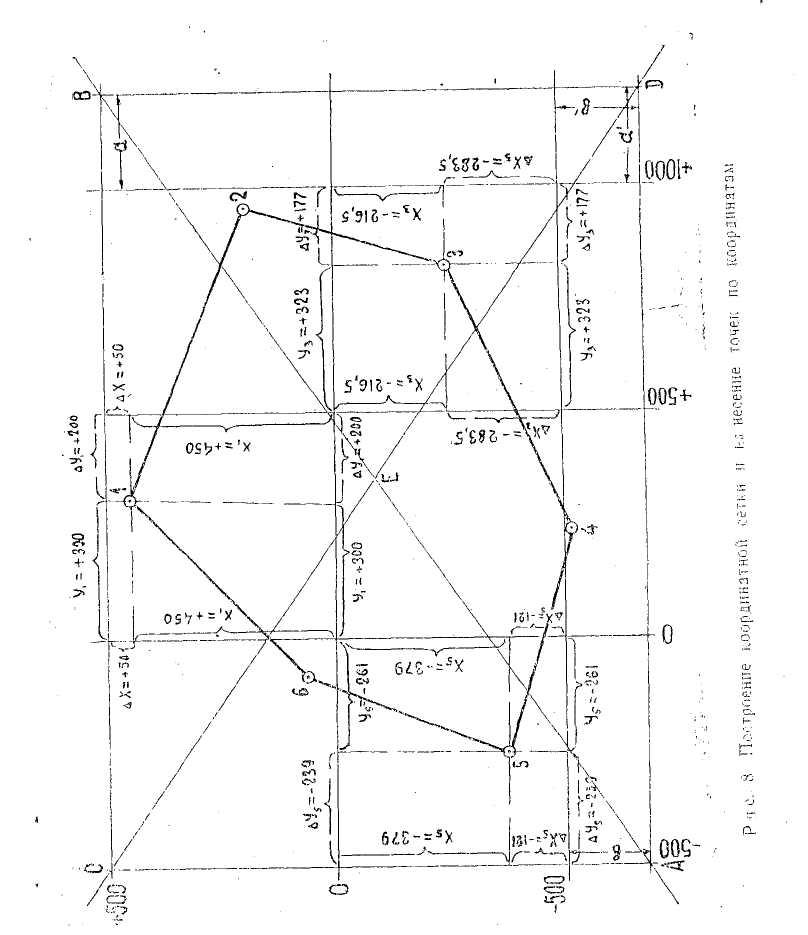
Рис. 2. Построение координатной сетки и нанесение точек по координатам

Оформление плана (рис. 3). Пересечение линий координатной сетки (кресты - 6 мм) и элементы гидрографии вычертить зеленой тушью, грунты - коричневой, все остальное - черной. Диагонали и другие вспомогательные карандашные линии, связанные с построениями, не вычерчивать.

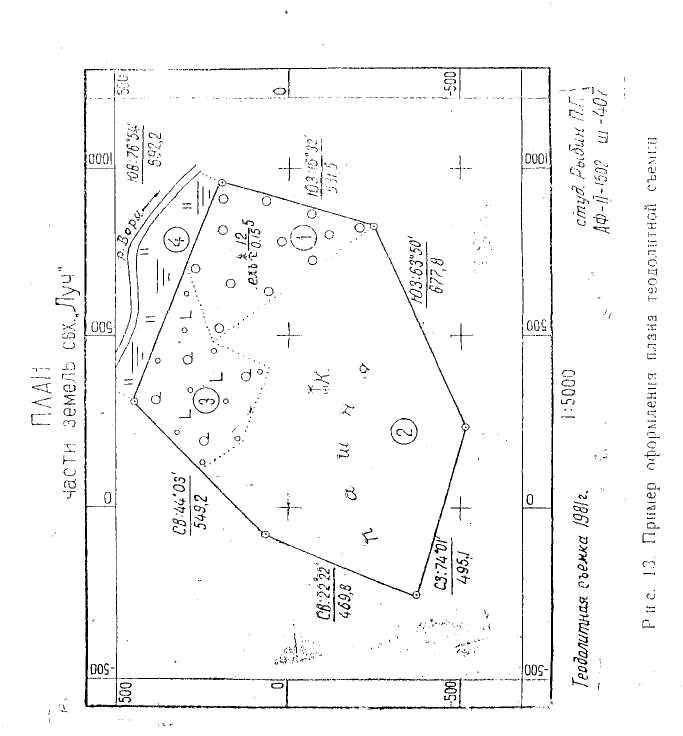
Рис. 3. Пример оформления плана теодолитной съемки