2.2. Линейное программирование в экономике

Приведем примеры некоторых типичных экономических и производственных задач, оптимальное решение которых может быть найдено с помощью построения и расчета соответствующих линейных математических моделей.

Планирование производства

Для изготовления различных видов изделий используются разные ресурсы. Общие запасы каждого ресурса, количество ресурса каждого типа, затрачиваемого на изготовление одного изделия каждого вида, и прибыль, получаемая от реализации одного изделия каждого вида, заданы. Нужно составить план производства изделий, обеспечивающий максимальную суммарную прибыль от реализации изделий.

Построение математической модели

Математическую модель строим по этапам, сформулированным в пункте 1.2.

1. Целью является максимизация прибыли.

2. Задача решается в общем виде, поэтому для определения параметров введем условные обозначения:

–число различных видов изделий;

– число различных типов ресурсов;

– запас ресурса -го типа,;

– количество ресурсов -ro типа для изготовления одного изделия -го вида,;;

– прибыль от реализации одного изделия -го вида.

3. Управляющие переменные число изделий-го вида.

4. Ограничения задачи – это ограничения по ресурсам и условия неотрицательности управляющих переменных.

Таким образом, можно построить математическую модель.

(2.2.1)

(2.2.2)

(2.2.1), (2.2.2) – линейная математическая модель поставленной задачи. В результате ее расчета определяют оптимальный план производства, т.е. количество изделий каждого вида, которые надо изготовить так, чтобы при этом была максимальна прибыль (2.2.1) и не был превышен запас ресурсов (2.2.2).

После изучения данного раздела целесообразно решить задачи 1-3 контрольной работы № 2, а также вернуться к решению задачи 7(если ее не удалось решить) из контрольной работы № 1

Формирование минимальной потребительской продовольственной корзины

Задан ассортимент продуктов, имеющихся в продаже. Каждый продукт содержит определенное количество разных питательных веществ (витаминов и калорий). Известен требуемый человеку минимум питательных веществ каждого вида. Необходимо опре­делить требуемую потребительскую продовольственную корзину, имеющую минимальную стоимость.

Составление математической модели.

1. Целью является минимизация стоимости потребительской корзины.

1. Параметры задачи:

–число различных продуктов, имеющихся в продаже;

–число различных питательных веществ, необходимых че­ловеку;

– содержание -го питательного вещества в-м продукте,;;

–количество -го питательного вещества, необходимое человеку,;

–стоимость единицы -го продукта,.

2. Управляющие переменные 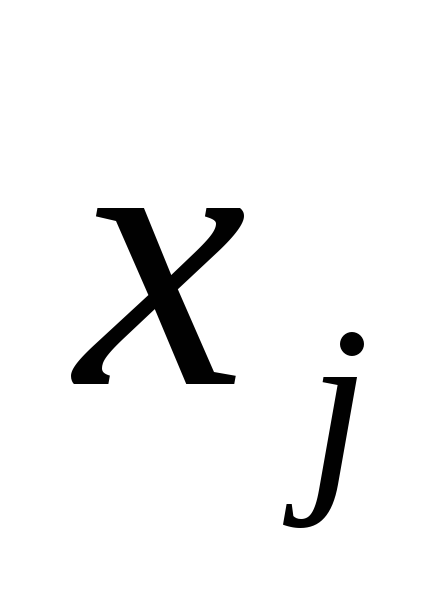– это количество-го продукта, входящего в потребительскую корзину,.

3. Область допустимых решений определяется следующей системой неравенств, содержащей условия по необходимому уровню потребления каждого питательного вещества во всех продуктах и условия неотрицательности управляющих переменных:

(2.2.4)

5) Критерий оптимальности имеет вид

(2.2.5)

(2.2.4), (2.2.5) – линейная математическая модель. После ее расчета определяют значения , удовлетворяющие ограничениям (2.2.4) и доставляющие минимум функции (2.2.5), т.е. рассчитывается состав минимальной потребительской продовольственной корзины.

После изучения данного раздела целесообразно решить задачи 4,5 контрольной работы № 2, а также вернуться к решению задачи 9(если ее не удалось решить) из контрольной работы № 1

Расчет оптимальной загрузки оборудования

Предприятию необходимо выполнить производственный заказ на имеющемся оборудовании. Для каждой единицы оборудования заданы: фонд рабочего времени, себестоимость на изготовление единицы продукции каждого вида и производительность, т.е. число единиц продукции каждого вида, которое можно произвести в единицу времени. Нужно распределить изготовление продукции между оборудованием таким образом, чтобы себестоимость всей продукции была минимальна.

Составление математической модели.

1. Целью является минимизация себестоимости.

2. Параметры:

– номенклатура, т.е. число различных видов продукции в производственном заказе;

– число единиц продукции -го вида,;

– число единиц оборудования;

– фонд времени работы оборудования -го типа,;

–производительность оборудования -го типа по производству изделий-го вида,;;

–себестоимость изготовления единицы продукции -го вида на оборудовании-го типа,;;

3) Управляющие переменные ,,– это время, в течение которого оборудование -го типа занято изготовлением продукции-го вида.

4) Область допустимых решений определяется ограничениями (2.2.6) по фонду времени, ограничениями (2.2.7) по номенклатуре и условиями неотрицательности .

(2.2.6) (2.2.7)(2.2.8)

5) Критерий оптимальности задается функцией

, (2.2.9)

где – суммарная себестоимость.

(2.2.6) – (2.2.9) – линейная математическая модель задачи. Она содержит неизвестных (управляющих переменных) и ограничений, не считая условий (2.2.8). После расчета модели определяется оптимальная загрузка оборудования, т.е. время в течение которого оборудование каждого типа занято изготовлением продукции каждого вида.

После изучения данного раздела целесообразно решить задачи 6-7 контрольной работы № 2.

Раскрой материала

На раскрой (распил) поступает материал нескольких видов в определенном количестве. Из этого материала необходимо изготовить различные изделия. Материал может быть раскроен разными способами. Каждый способ имеет свою себестоимость и позволяет получить разное количество изделий каждого вида. Определить способ раскроя, при котором суммарная себестоимость минимальна.

Составление математической модели.

1. Цель – минимизация себестоимости раскроя.

2. Параметры:

– число различных видов материала, поступающего на раскрой;

– количество материала -го вида,;

– число различных видов изделий, которые надо изготовить;

– исло изделий -го вида,;

– число различных способов раскроя;

–исло изделий -го вида, которое можно получить изединицы материала -го вида при-м способе раскроя,,,;

–ебестоимость раскроя единицы материала -го вида-м способом, ,.

3) Управляющие переменные – количество единиц материала-го вида, раскраиваемых-м способом, ,.

4) Область допустимых решений определяется ограничениями по количеству исходного материала (2.2.10), ограничениями по выпуску (2.2.11) и условиями неотрицательности управляющих переменных (2.2.12).

(2.2.10)(2.2.11)(2.2.12)

4. Критерий оптимальности задается формулой

(2.2.13)

(2.2.10) – (2.2.13) – линейная математическая модель поставленной задачи. Она содержит неизвестных (управляющих переменных) и ограничений, не считая условий неотрицательности переменных . После расчета модели определяется количество материала каждого вида, раскраиваемого различными способами.

Вместо критерия минимизации себестоимости в задаче может быть взят, например, критерий минимизации отходов. В этом случае в условии должно быть задано количество отходов, получаемых при каждом способе раскроя для единицы материала каждого вида.

После изучения данного раздела целесообразно решить задачи 8-11 контрольной работы № 2.

Составление плана реализации товара

Фирма реализует различные товары, используя при этом определенный набор средств (технических, людских, денежных).

Общий запас средств, число средств каждого вида, используемых при реализации единицы любого товара и прибыль от его продажи заданы. Надо сформировать план реализации товаров, приносящий фирме максимальную прибыль.

Построение математической модели.

1. Цель — максимизации прибыли.

2. Параметры:

– число различных видов реализуемых товаров;

– число разных видов средств;

– запас средств -го вида,;

–число средств -го вида, используемых для реализации единицы товара-го вида,,;

– прибыль от реализации единицы товара -го вида,.

3. Управляющие переменные ,– количество реализуемого товара-го вида;

4. Область допустимых решений формируют ограничения по запасам средств и условия неотрицательности управляющих переменных.

(2.2.14)

5) Критерий оптимальности определяется по формуле

, (2.2.15)

где – суммарная прибыль.

В результате расчета линейной математической модели (2.2.14), (2.2.15) определяется количество реализуемых товаров каждого вида, обеспечивающее фирме максимальную прибыль.

После изучения данного раздела целесообразно решить задачи 12-13 контрольной работы № 2.