1.3. Примеры построения математических моделей экономических задач

Рассмотрим следующую задачу.

Предприятие располагает определенными производственными мощностями для изготовления изделий и может выпускать изделия фиксированных наименований для их последующей реализации. Требуется определить оптимальный состав производственного заказа и способы его изготовления.

Построение математической модели.

1. Цель:

• максимизация прибыли от реализации;

• минимизация себестоимости изготовления;

• минимизация времени обработки.

Выходные переменные модели Y: прибыль от реализации (Y1),

себестоимость изготовления (Y2), время обработки (Y3).

2. Параметры модели (постоянные параметры A):

• –число единиц оборудования;

• – число наименований изделий, которое может выпускать предприятие;

• –фонд времени работы i-й единицы оборудования ;

• – число различных способов изготовления изделия -гo наименования, характеризующихся различным временем обработки на единице оборудования -го типа;

• – время обработки изделия -го наименования, изготавливаемого -м способом на оборудовании-го типа ;

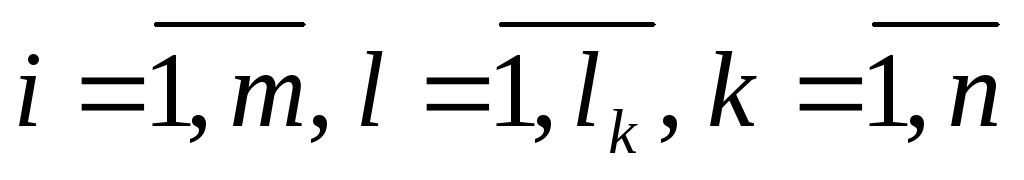• –спрос на изделие -го наименования;

• –размер склада, предусмотренного для хранения изделий, выраженный в количествах изделий;

• –себестоимость изготовления изделия -го наименования -м способом ;

• – требуемая себестоимость изготовления изделия -го наименования ;

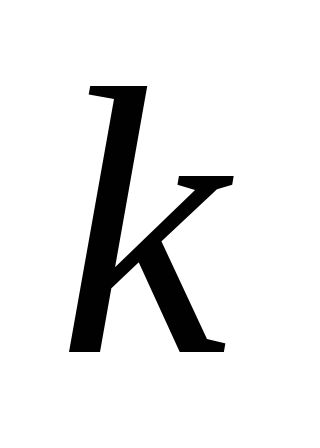• –прибыль от реализации изделия -го наименования ;

3. Управляющие переменные X:

– число изделий -го наименования, выпускаемыхl-м способом ;

4. Определение области допустимых решений (системы ограничений φ):

, (1.3.1)

–ограничение по фонду работы оборудования;

–ограничение по размеру склада; (1.3.2)

–ограничение по спросу; (1.3.3)

–ограничение по себестоимости изготовления; (1.3.4.)

1.3.5.)

5. Выражение критерия эффективности через параметры и управляющие переменные модели.

1) Максимизация прибыли.

Y1 - суммарная прибыль.

(1.3.6)

2) Минимизация себестоимости.

Является критерием при отсутствии ограничения (1.3.4).

(1.3.7)

3) Минимизация суммарного времени обработки Y3, выраженного, например, в станко-часах.

(1.3.8)

Таким образом, построены три однокритериальные линейные модели:

(1.3.1) – (1.3.6) – формирование производственного заказа по критерию максимизации прибыли;

(1.3.1) – (1.3.3), (1.3.5), (1.3.7) – организация производственного процесса по критерию минимальной себестоимости изготовления;

(1.3.1) – (1.3.5), (1.3.8) - организация производственного процесса по критерию минимального времени изготовления.

Если прибыль нелинейно зависит от числа выпускаемых изде­лий,

, (1.3.10)

где – некоторая нелинейная функция, то переходим к нелинейной оптимизационной модели (1.3.1) – (1.3.5), (1.3.10).

Модель (1.3.1) – (1.3.5), (1.3.6), (1.3.8) является многокритериальной.

Решениями исходной задачи, получаемыми в результате расчета любой из предложенных моделей, служат значения переменных ;;, которые удовлетворяют ограничениям, сформулированным в пункте 4, и доставляют экстремум одному или нескольким выбранным критериям оптимизации.

После изучения раздела 1 следует выполнить контрольную работу № 1.