4.2 Геометрическая интерпретация задачи нелинейного программирования. Графический метод решения

Рассмотрим задачу Нелинейного программирования, содержащую две переменные.

(4.2.1)

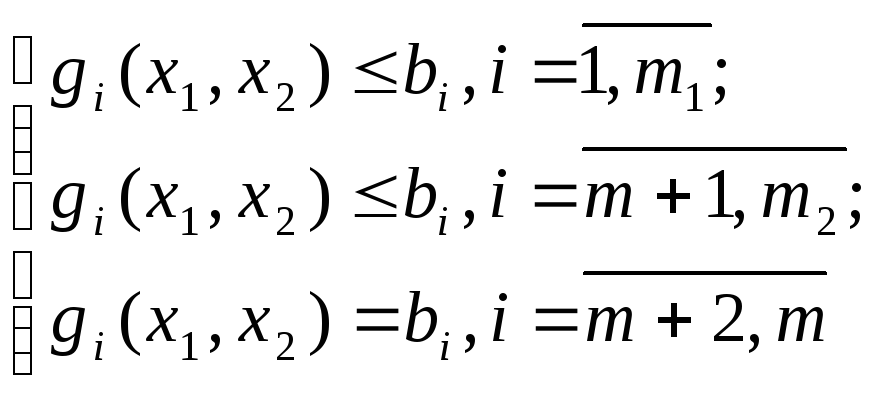(4.2.2)

Система ограничений (4.2.2) определяет в -мерном пространстве некоторую область, которая является областью допустимых решений задачи.

Решить ЗНП графически – это значит найти точку области допустимых решений (4.2.2), через которую проходит линия наивысшего (наинизшего) уровня.

Указанная точка может находиться как на границе, так и внутри области допустимых решений (4.2.2), в отличие от задач линейного программирования.

Так же, как и для линейных задач, ЗНП удобно решать графически, когда функция и ограничения содержат две переменные.

Алгоритм решения ЗНП графическим методом

Шаг 1. На плоскости строят область допустимых решений, определенную ограничениями (4.2.2). Если она пуста, т.е. ограничения несовместны, то задача (4.2.1) – (4.2.2) не имеет решения. В противном случае переходят к шагу 2.

Шаг 2. Строят линию уровня функции , где С – некоторая константа. Переход к шагу 3.

Шаг 3. Определяют направление возрастания (при максимизации), убывания (при минимизации) функции .

Шаг 4. Находят точку области допустимых решений, через которую проходит линия уровня с наибольшим (при максимизации), наименьшим (при минимизации) значением С или устанавливают неограниченность функции на области допустимых решений.

Шаг 5. Определяют значения для точки, найденной на шаге 4, и величину функции в этой точке.

Пример 4.2.1

В соответствии с алгоритмом построим на плоскости область допустимых решений (рис. 4.2.1)

Рис. 4.2.1

Ограничения , выделяют на плоскости первую четверть.

Границей полуплоскости, соответствующей первому ограничению,

является гипербола

Неравенство выполняется для точек, лежащих выше гиперболы.

Границей полуплоскости, определяемой вторым ограничением, является окружность с центром в точке (0,0) и радиусом, равным 4. Искомая полуплоскость заштрихована вертикальной штриховкой. Область допустимых решений выделена горизонтальной штриховкой.

Функция возрастает в направлении вектора-нормали с координатами (2,3), и ее линии уровня расположены перпендикулярно вектору-нормали. Таким образом, максимум достигается в точкеА, а минимум – в точке В.

Заметим, что в точке А совпадают тангенсы углов наклона касательной к окружности и прямойк оси . Тангенсы углов наклона касательной и прямой к оси определяются значениями производных по соответствующих функций. Для прямойтангенс равен.

Продифференцируем выражение как неявную функцию от. Получаем

,

Приравниваем значения тангенсов, получаем

,

К этому уравнению добавим уравнение окружности, которой принадлежит точка А.

Получаем систему

Решив ее, найдем оптимальное решение

; ;

Аналогично определим координату точки В, в которой тангенс угла наклона к оси прямой совпадает с тангенсом угла наклона касательной к функции.

Получаем уравнение

Вторым для нахождения координат точки является уравнение гиперболы, которой принадлежит точка В:

Из последней системы найдем оптимальное решение, соответствующее минимальному значению ,

, ,