
- •1. Сущность математического моделирования экономических процессов
- •1.1. Понятие математической модели экономического процесса
- •1.2. Классификация математических моделей
- •1.3. Примеры построения математических моделей экономических задач
- •2. Линейное программирование
- •2.1. Постановка задачи линейного программирования
- •2.2. Линейное программирование в экономике
- •2.3. Графический метод решения задачи линейного программирования
- •2.4. Основная задача линейного программирования
- •2.5.Симплекс-метод
- •2.6.Пример расчета экономико-математической модели
- •2.7. Двойственная задача линейного программирования. Экономическая интерпретация
- •2.8. Целочисленное линейное программирование. Метод Гомори
- •3. Транспортная задача как пример специальной задачи линейного программирования
- •3.1.Построение транспортной модели
- •3.2. Сбалансированные и несбалансированные транспортные модели
- •3.3. Определение начального плана транспортировок. Методы "северо-западного" угла, минимального элемента, Фогеля
- •3.4.Оптимальный план транспортной задачи. Метод потенциалов
- •3.5. Экономические задачи, сводящиеся к транспортным моделям
- •3.6. Венгерский метод решения задачи о назначениях
- •3.7. Применение задачи о назначениях к решению экономических проблем
- •4. Нелинейное программирование
- •4.1. Постановка задачи нелинейного программирования
- •4.2 Геометрическая интерпретация задачи нелинейного программирования. Графический метод решения
- •4.3. Метод множителей Лагранжа
- •4.4. Расчет экономико-математической модели при нелинейных затратах на производство
- •5. Динамическое программирование
- •5.1. Постановка задачи динамического программирования. Основные условия и область применения
- •5.2. Составление математической модели динамического программирования
- •5.3.Этапы решения задачи динамического программирования
- •5.4. Задача замены оборудования как задача динамического программирования
- •5.5. Оптимальное распределение инвестиций как задача динамического программирования
- •6. Модели систем массового обслуживания
- •6.1 Определение систем массового обслуживания
- •6.2 Классификация смо.
- •6.3. Параметры смо
- •6.4 Модели смо с отказами.
- •6.5 Модели смо с неограниченным временем ожидания
- •6.6 Модели замкнутых смо
- •7. Модели сетевого планирования и управления (спу)
3.7. Применение задачи о назначениях к решению экономических проблем
Выше уже был дан пример применения задачи о назначениях к проблеме оптимального выбора руководителей исследовательских проектов. Приведем еще несколько примеров, когда использование задачи о назначениях позволяет найти оптимальное решение экономической задачи.
Оптимальное исследование рынка
Группе,
исследующей рынок, требуется получить
данные из
![]() различных мест. В ее распоряжении имеется
различных мест. В ее распоряжении имеется![]() дней, и она предполагает провести по
одному дню в каждом месте, проведя по
дней, и она предполагает провести по
одному дню в каждом месте, проведя по![]() опросов,
опросов,
![]() .
Вероятность успешного опроса в каждом
месте задается матрицей
.
Вероятность успешного опроса в каждом
месте задается матрицей![]() .
Элемент
матрицы
.
Элемент
матрицы
![]() характеризует
вероятности успешного опроса в течение
характеризует
вероятности успешного опроса в течение
![]() -го
дня в
-го
дня в![]() -м
месте,
-м
месте,![]() ;
;![]() .
.
Определить время проведения опросов, при котором общее число опросов максимально.
Решение
Сведем данную задачу к задаче о назначениях.
Введем
величину
![]() ,
показывающую
число успешных опросов в
,
показывающую
число успешных опросов в
![]() -м
месте в течение
-м
месте в течение![]() -го
дня.
-го
дня.
![]()
Математическая модель задачи имеет следующий вид:
![]()

Функция
![]() характеризует
суммарное число опросов. Его нужно
максимизировать. Первое и второе
ограничения соответствуют тому, что в
течение одного дня можно находиться
только в одном месте. Для расчета модели
венгерским методом надо перейти к
противоположной функции
характеризует
суммарное число опросов. Его нужно
максимизировать. Первое и второе
ограничения соответствуют тому, что в
течение одного дня можно находиться
только в одном месте. Для расчета модели
венгерским методом надо перейти к
противоположной функции
![]() ,
,
и в
соответствующей таблице записывать
значения
![]() с противоположным знаком.
с противоположным знаком.
Оптимальное использование торговых агентов
Торговая
фирма продает товары в
![]() различных городах, покупательная
способность жителей которых оценивается
в
различных городах, покупательная
способность жителей которых оценивается
в![]() усл.
ед.,
усл.
ед.,
![]() .
Для
реализации товаров фирма располагает
.
Для
реализации товаров фирма располагает
![]() торговыми агентами, каждого из которых
она направляет в один из городов.
Профессиональный уровень агентов
различен; доля реализуемых
торговыми агентами, каждого из которых
она направляет в один из городов.
Профессиональный уровень агентов
различен; доля реализуемых![]() -м
торговым агентом покупательных
способностей составляет
-м
торговым агентом покупательных
способностей составляет![]() ,
,
![]() .Как
следует распределить торговых агентов
по городам, чтобы фирма получила
максимальную выручку от продажи товаров?
.Как
следует распределить торговых агентов
по городам, чтобы фирма получила
максимальную выручку от продажи товаров?
Решение.
Оптимальное решение этой проблемы может быть найдено с помощью задачи о назначениях. В качестве кандидатов выступают торговые агенты, в качестве работ – города.
Введем
параметр
![]() ,
характеризующий
величину покупательных способностей,
реализуемых
,
характеризующий
величину покупательных способностей,
реализуемых
![]() -м
торговым агентом в
-м
торговым агентом в![]() -м
городе.
-м
городе.
Управляющие
переменные
![]() ,
,
![]() ,
,
![]() определяются по формуле
определяются по формуле
![]()
Математическая модель запишется в следующей форме:
![]()
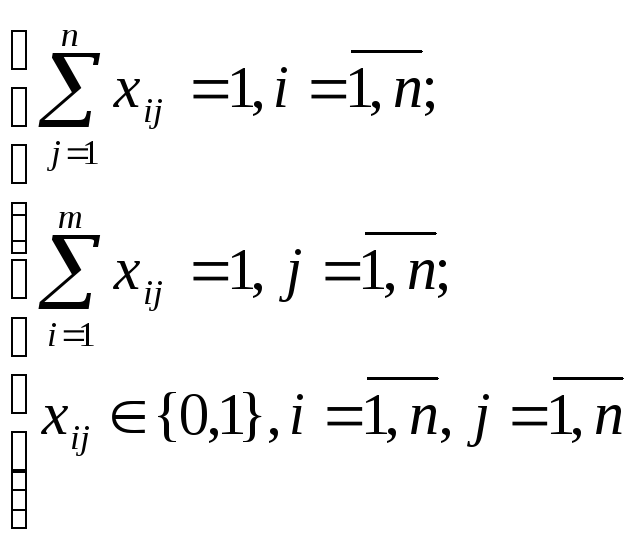
Первое и второе ограничения формализуют соответственно условия о том, что в каждый город направляется один торговый агент, и один торговый агент не может работать в двух городах. Целевая функция С – это сумма реализованных покупательных способностей всеми торговыми агентами во всех городах. Она должна быть максимальна. Для решения задачи венгерским методом надо, как и в предыдущем примере, перейти к противоположной функции.
4. Нелинейное программирование
4.1. Постановка задачи нелинейного программирования
В общем виде задача нелинейного программирования (ЗНП) формулируется следующим образом:
![]() (4.1.1)
(4.1.1)
 (4.1.2)
(4.1.2)
где
![]() – управляющие
переменные или решения ЗНП,
– управляющие
переменные или решения ЗНП,
![]() ;
;
![]() – фиксированные
параметры,
– фиксированные
параметры,
![]() ;
;
![]() ,
,
![]() ,
,![]() –
заданные функции от
–
заданные функции от
![]() переменных.
переменных.
Если
![]() и
и
![]() линейны,
то (4.1.1), (4.1.2) переходит в задачу линейного
программирования.
линейны,
то (4.1.1), (4.1.2) переходит в задачу линейного
программирования.
Решить
задачу нелинейного программирования
– это значит найти такие значения
управляющих переменных
![]() ,
,
![]() ,
которые
удовлетворяют системе ограничений
(4.1.2) и доставляют максимум или минимум
функции
,
которые
удовлетворяют системе ограничений
(4.1.2) и доставляют максимум или минимум
функции
![]() .
.
Для задачи нелинейного программирования, в отличие от линейных задач, нет единого метода решения. В зависимости от вида целевой функции (4.1.1) и ограничений (4.1.2) разработано несколько специальных методов решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программирование, градиентные методы, ряд приближенных методов решения, графический метод.
Заметим, что нелинейное моделирование экономических задач часто бывает довольно искусственным. Большая часть экономических проблем сводится к линейным моделям, поэтому в данном пособии нелинейные модели и методы расчета рассмотрены достаточно кратко.
