
dm_tema_1
.pdf
Дискретная математика Тема 1. Теория множеств
Е.А.Перепелкин
АлтГТУ
2012
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
1 / 65 |
1. Теория множеств |
1.1 Понятие множества |
1.1 Понятие множества
Понятие множества является первичным неопределяемым понятием математики. Множество можно понимать как объединение элементов, обладающих заданным свойством. Принадлежность элемента x
множеству A обозначается как x 2 A, непринадлежность как x 2= A. Способы задания множеств:
1) Перечислением элементов конечного множества
A= fx1; x2; : : : ; xng
2)Характеристическим свойством
A= fxj P(x)g
3)Алгоритмом формирования элементов множества.
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
2 / 65 |

1. Теория множеств |
1.1 Понятие множества |
Пример
Множество цифр шестнадцатеричной системы счисления зада¼тся перечислением цифр
X = f0; 1; 2; 3; 4; 5; 6; 7; 8; 9; A; B; C ; D; E ; F g:
Множество точек окружности единичного радиуса зада¼тся
уравнением
S = f(x; y)j x2 + y2 = 1g:
Множество натуральных ч¼тных чисел от 0 до n можно задать алгоритмом формирования этих чисел
begin
k=0; M={0}; while k<=n do
k:=k+2; M={M, k} end
end
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
3 / 65 |

1. Теория множеств 1.1 Понятие множества
Для числовых множеств приняты следующие обозначения: N множество натуральных чисел;
Z множество целых чисел;
Q множество рациональных чисел;
R множество действительных чисел;
C множество комплексных чисел. Интервал на числовой оси обозначается как
(a; b) = fxj a < x < bg:
Полуинтервалы
(a; b] = fxj a < x bg; [a; b) = fxj a x < bg:
Отрезок
[a; b] = fxj a x bg:
Промежуток любое из указанных множеств: интервал, полуинтервал или отрезок. 







Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
4 / 65 |

1. Теория множеств |
1.1 Понятие множества |
В теории множеств известны парадоксы логические противоречия. Например, парадокс Рассела.
Рассмотрим множество всех множеств, не содержащих себя в качестве элемента
A = fBj B 2= Bg :
Пусть A 2 A. Тогда A 2= A. Пусть A 2= A. Тогда A 2 A. Получили
противоречие.
Устранить подобного рода противоречия можно с помощью системы аксиом или ограничив элементы множества некоторым заданным множеством U, которое принято называть универсальным множеством
или универсумом,
A = fx 2 Uj P(x)g :
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
5 / 65 |

1. Теория множеств 1.2 Операции над множествами
1.2 Операции над множествами
Обозначим: U универсум; A; B; C; ::: подмножества U; ; пустое множество.
Определение
Множество A является подмножеством B (A включается в B), åñëè
8x 2 U : x 2 A ) x 2 B:
Включение обозначают A B. Строгое включение A B означает, что A B è A 6= B.
Два множества равны (совпадают), A = B, если они являются подмножествами друг друга: A B è B A, или справедливо
утверждение
x 2 A , x 2 B:
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
6 / 65 |

1. Теория множеств |
1.2 Операции над множествами |
Основные операции над множествами:
1) Объединение
A [ B = fxj x 2 A èëè x 2 Bg
2) Пересечение
A \ B = fxj x 2 A è x 2 Bg
3) Разность
A n B = f xj x 2 A è x 2= Bg
4) Симметрическая разность
A 4 B = fxj (x 2 A è x 2= B) èëè (x 2= A è x 2 B) g
A 4 B = (A n B) [ (B n A)
A 4 B = (A [ B) n (A \ B)
5) Дополнение
A = fxj x 2= Ag
A = U n A
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
7 / 65 |
1. Теория множеств |
1.2 Операции над множествами |
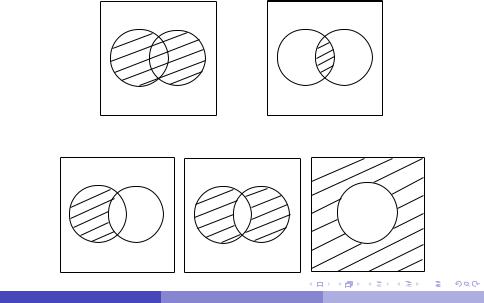
Наглядное представление операций над множествами дают диаграммы Эйлера-Венна
A |
|
B |
A |
B |
|
|
A B |
|
|
A ∩ B |
|
A |
B |
A |
B |
A |
|
|
|
|
|
¯ |
|
A \ B |
|
|
A 4 B |
A |
|
|
|
|
|
||
Е.А.Перепелкин (АлтГТУ) |
|
Дискретная математика. Тема 1 |
2012 |
8 / 65 |
|

1. Теория множеств |
1.2 Операции над множествами |
Определение
Разбиением множества A называется набор его попарно непересекающихся подмножеств Ai , i 2 I таких, что
[
A = Ai ; Ai \ Aj = ;; i 6= j:
i2I
Определение
Булеаном множества A называется множество всех его подмножеств
2A = fBj B Ag :
Пустое множество ; и само множество A являются элементами булеана.
Пример
Для множества A = fx; y; zg
2A = f;; fxg; fyg; fzg; fx; yg; fx; zg; fy; zg; fx; y; zgg:
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
9 / 65 |

1. Теория множеств |
1.2 Операции над множествами |
Определение
Характеристической функцией множества A называется функция принадлежности элементов U множеству A
1; x 2 A fA(x) = 2
0; x = A
Множества совпадают тогда и только тогда, когда совпадают их характеристические функции
A = B , fA(x) = fB (x):
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
10 / 65 |
