гидравлика методичка

Лабораторная работа № 6

Иллюстрация уравнения Бернулли

6.1 Цель и задача лабораторной работы

Цель – опытное подтверждение уравнения Д.Бернулли, т.е. понижения механической энергии по течению и перехода потенциальной энергии в кинетическую и обратно (связь давления со скоростью).

Задача – измерить пьезометрические напоры в каналах постоянного и переменного сечений;

–построить пьезометрическую линию для каналов постоянного и переменного сечений;

–построить напорную линию для канала переменного сечения;

–выявить закономерности изменения напоров от поперечных сечений каналов.

Результат работы представляется в виде таблицы расчетных величин, пьезометрических и напорной линий для каналов постоянного и переменного сечений.

6.2 Основные теоретические положения

Уравнение Д.Бернулли выражает закон сохранения энергии и для двух сечений потока реальной капельной жидкости в упрощённом виде записывается так:

гидравлических сил трения между сечениями 1-1 и 2-2;

61

индексы «1» и «2» указывают номер сечения, к которому относится величина.

Слагаемые уравнения выражают энергии, приходящиеся на единицу веса (силы тяжести) жидкости, которые в гидравлике принято называть напорами:

z – геометрический напор (потенциальная энергия положения);

p = H – пьезометрический напор (потенциальная ρg п

– потери напора (механической энергии). Такие энергии измеряются в единицах длины.

Из уравнения следует, что в случае отсутствия теплообмена потока с внешней средой полная удельная энергия (включая тепловую) неизменна вдоль потока, и поэтому изменение одного вида энергии приводит к противоположному по знаку изменению другого. Таков энергетический смысл уравнения Бернулли. Например, при расширении потока скорость V и, следовательно,

2g

сохранения баланса вызывает увеличение потенциальной

p

энергии ρg

потока по течению приводит к возрастанию давления, и наоборот.

62

6.3 Схема установки и методика измерений

Устройство №4 содержит баки 1 и 2, сообщаемые через опытные каналы переменного 3 и постоянного 4 сечений (рисунок 6.1). Каналы соединены между собой равномерно расположенными пьезометрами I-V, служащими для измерения пьезометрических напоров в характерных сечениях. Устройство №4 заполнено подкрашенной водой. В одном из баков пре6дусмотрена шкала 5 для измерения уровня воды.

При перевёртывании устройства №4, благодаря постоянству напора истечения Н0 во времени, обеспечивается установившееся движение воды в нижнем канале. Другой канал в это время пропускает воздух, вытесняемый жидкостью из нижнего бака в верхний.

Работу с устройством №4 выполнить в следующей последовательности:

1) При заполненном водой баке 2 (рисунок 6.1) перевернуть устройство №4 для получения течения в канале переменного сечения 3.

частям менисков воды в них.

3) Измерить время t перемещения уровня в баке на произвольно заданную величину S.

6.4 Обработка результатов

По размерам А и В поперечного сечения бака, перемещению уровня S и времени t определить расход Q воды в канале, а затем скоростные Hк и полные Н напоры в сечениях канала по порядку, указанному в таблице 6.1.

Вычертить в масштабе канал с пьезометрами (рисунок 6.2). Соединив уровни жидкости в пьезометрах и центром выходного сечения VI, получить пьезометрическую линию 1, показывающую изменение

63

потенциальной энергии (давления) вдоль потока. Для получения напорной линии 2 (линии полной механической энергии) отложить от оси канала полные напоры Н и соединить полученные точки.

1,2 – баки; 3,4 – опытные каналы переменного и постоянного сечений; 5 – уровнемерная шкала; I-V –

пьезометры Рисунок 6.1 - Схема устройства №4

64

Таблица 6.1 – Результаты опытов

Q=ABS/t=….. см3/с

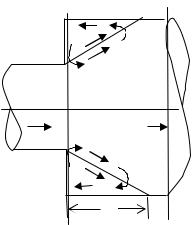
1,2 – пьезометрическая и напорная линии; Н1 и Н2 – полные

напоры (механические энергии) на входе и выходе из канала; hТР, hд1, hд2, hВС, hР, hС – потери напора: суммарные, по длине на

1ом и 2ом участках, на внезапное сужение, на плавные расширение и сужение

65

Рисунок 6.2 - Иллюстрация уравнения Бернулли

6.5 Анализ полученных результатов и вывод

Проанализировать изменение полной механической

жидкости вдоль потока; выяснить соответствие этих изменений уравнению Бернулли.

В выводах сделать заключения о влиянии на величины напоров площадей поперечных сечений каналов, изменений этих площадей.

6.6 Контрольные вопросы

1)Виды гидравлических сопротивлений.

2)Потери напора на трение в круглых трубах.

3)Потери напора, связанные с изменением сечения

потока.

66

Лабораторная работа № 7

Определение местных потерь напора

7.1 Цель и задача лабораторной работы

Цель – исследование потерь напора на преодоление местных сопротивлений.

Задача – опытным путём определить значения местных потерь для результатов измерений предыдущей лабораторной работы для канала переменного сечения;

–определить коэффициенты местного сопротивления для различных участков воздуховода;

–сравнить полученные результаты со справочными значениями;

–определить взаимовлияние частей трубопровода.

Результат работы представляется в виде таблиц расчетных величин, суммарных значений коэффициентов местных сопротивлений.

7.2 Основные теоретические положения

Местные потери напора (энергии) жидкости возникают на коротких участках трубопровода с препятствиями для потока, называемыми местными сопротивлениями. Местные сопротивления вызываются фасонными частями, арматурой, другим оборудованием трубопроводов. Это оборудование вызывает изменение величины или направления скорости движения на отдельных участках трубопровода (при расширении или сужении потока, из-за поворота, при протекании через диафрагмы, задвижки и т.п.), что связано с появлением дополнительных потерь напора.

В водопроводных трубопроводах потери напора на местные сопротивления обычно невелики и составляют не более 10-20% от потерь напора на трение. В воздухопроводах вентиляционных и пневмотранспортных

67

установок, в дутьевых установках котельных потери на преодоление местных сопротивлений часто значительно больше потерь напора на трение. Местные сопротивления являются весьма существенными также при расчете трубопроводов.

Величину потери напора, затраченной на преодоление какого-нибудь местного сопротивления, принято оценивать в долях от скоростного напора, соответствующего скорости непосредственно за рассматриваемым местным сопротивлением. Она определяется из формулы Вейсбаха:

сопротивления.

Коэффициенты различных местных сопротивлений ζ находятся обычно опытным путем. Таблицы этих значений (или эмпирические кривые и формулы для них) содержатся в инженерных справочниках и руководствах по гидравлике. Для некоторых практически важных случаев значения коэффициентов местных сопротивлений удается получить также теоретическим путем.

Иногда местные потери выражаются в виде эквивалентной длины lэ прямого участка трубопровода, сопротивление которого по величине равно рассматриваемым местным потерям напора. Используется условие:

Коэффициент гидравлического трения λ зависит от числа Рейнольдса и относительной шероховатости. Поэтому одному и тому же значению коэффициента

68

от стенок и дальше движется в виде свободной струи, отделенной от стальной жидкости поверхностью раздела (рисунок 7.1). Поверхность раздела неустойчива, на ней возникают вихри, в результате чего происходит перемешивание транзитной струи с окружающей жидкостью. Струя постепенно расширяется и на некотором расстоянии l от начала расширения заполняет все сечение широкой трубы. Из-за отрыва потока и связанного с этим вихреобразования происходят значительные потери напора.

Величину этих потерь можно найти, решая уравнение Бернулли для сечений в месте расширения 1-1 и после заполнения потоком всего поперечного сечения трубы 2-2:

Получаемое решение (7.4) носит название теоремы