
Высшая математика
.pdf
Свойство 5.
ar ar = |
|
ar |
|
2 cos 0 = |
|
ar |
|
2 |
|
ar |
|
= ar ar . |
(7) |
|
|
|
|
|
|
Свойство 6. Критерий перпендикулярности векторов:
r |
v |
v |
= 0 . |
(8) |
a |
b a |
b |
Доказательство этого свойства советуем провести самостоятельно.
2.1.2 Вычисление скалярного произведения в координатной форме
Пусть известны координаты векторов av = {ax ; ay ; az } и br = {bx ; by ; bz } .
Найдём скалярное произведение этих векторов.
ar br = ( ax ir+ ay rj + az kr ) ( bx ir+ by rj + bz kr ) = по свойствам 3 и 4 =
= axbx ir ir+ axb y ir j + axbz iv kv + aybx vj iv+ ayby vj vj + aybz rj kr + azbx kr ir+ +azby kr rj + azbz kr kr = по свойствам 5 и 6 = axbx + ayby + azbz .
Таким образом, получена важная формула:
|
ar b = axbx + ayby + azbz . |
(9) |
|
|
|
uur |
r |
Пример 8. Вычислить скалярное произведение векторов AB |
и a , если |
||
|
А(1; 2; –1), В(0; 3; 2), ar |
= j − kr. |
|
|
uuur |
a = {0; 1; –1}. |
|
• |
AB = {0 – 1; 3 – 2; 2 – (–1)} = {–1; 1; 3}, |
||
uur r
По формуле (8) вычисляем AB a = (–1) 0 + 1 1 + 3 (–1) = –2. •
2.1.3 Приложения скалярного произведения
1. Вычисление длины вектора
Если a = { ax ;ay ;az } , то согласно формулам (7) и (9) имеем:
|
|
|
|
|
ar |
|
= |
ax2 + a2y + az2 . |
(10) |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
uur |
|
Задача 3. Найти длину вектора |
AB , если A( xA ; yA ; zA ), B( xB ; yB ; zB ). |
||||||||
Или, что то же, найти расстояние между точками А и В. |
|
||||||||
|
uuur |
|
|
|
|
|
|
||
• |
AB = {xB − xA ; yB − yA ; zB − zA} . Согласно (10) имеем: |
|
|||||||
|
|
uuur |
|
(xB − xA )2 +( yB − yA )2 +(zB − zA )2 . |
|
||||
|
|
AB |
= AB = |
• (11) |
|||||
Пример 9. Найти длину медианы AD в треугольнике АВС, если
А(2; 1; 0), В(–2; 2; 1), С(0; 4; 1).
61
• Точка D – серединная точка отрезка ВС, поэтому |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x |
B |
+ x |
y |
B |
+ y |
z |
B |
+ z |
|
−2 +0 |
|
2 + |
4 |
|
|
1 |
+ 1 |
|
|
||||||||
D |
|
C |
; |
|
C |
; |
|
C |
|
D |
|
; |
|
|
|
; |
|
|
|
|
D( −1; 3; 1 ). |
||||||
|
|
2 |
|
|
2 |
|
|
2 |
2 |
|
2 |
|
|
|
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
AD = (xD − xA )2 + ( yD − y A )2 + ( zD − zA )2 = |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
= (−1 − 2)2 + ( 3 − 1 )2 + ( 1 − 0 )2 = 9 + 4 + 1 = 14 . • |
|
|
|||||||||||||||||||||||
2. Нахождение угла между векторами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Из формулы (5) можно получить |
|
|
|
|
ar b |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r r |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
cosϕ = cos ( a ,b ) |
= |
r |
|
|
r |
|
. |
|
|
(12) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
r |
|
||||
Зная косинус угла, можно получить сам угол. Заметим, |
|
r |
> 0 , то |
||||||||||||||||||||||||
что если a |
b |
||||||||||||||||||||||||||
r |
r |
|
|
|
|
|
|
|
|
|
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
( a ,b ) − острый угол, если же |
a |
b < 0 , то ( a ,b ) − тупой. |
|
|
|||||||||||||||||||||||
Пример 10. Найти внутренний угол В в треугольнике, вершины которого зада-
ны координатами |
А(–1; –2; 4), В(–4; –2; 0), |
С(3; –2; 1). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
uur |
−( |
−4 ); − 2 −( −2 ); 4 |
−0} ={3; 0; 4} |
|
|
|
и |
||||||||||||||||
• |
Рассмотрим векторы BA ={−1 |
|
|
|
||||||||||||||||||||||
uur |
={3 −( −4 ); |
− 2 −( −2 ); 1 −0} |
= |
{7 ; 0; 1} . |
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
uuur uuur |
|
uur |
uuur |
|
|
|
3 7 + 0 |
0 + 4 1 |
|
|
|
|
|
|
1 |
|
||||||||
|
|
|
BA BC |
|
|
|
|
|
|
|
|
|
|
= |
|
|
||||||||||
cos B = cos ( BA, BC ) |
= | BC | | BC | = |
32 +02 + 42 |
7 2 +02 +12 |
|
2 . |
|||||||||||||||||||||
|
|
|
|
uuur |
uuur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда следует, что B = 45°. • |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
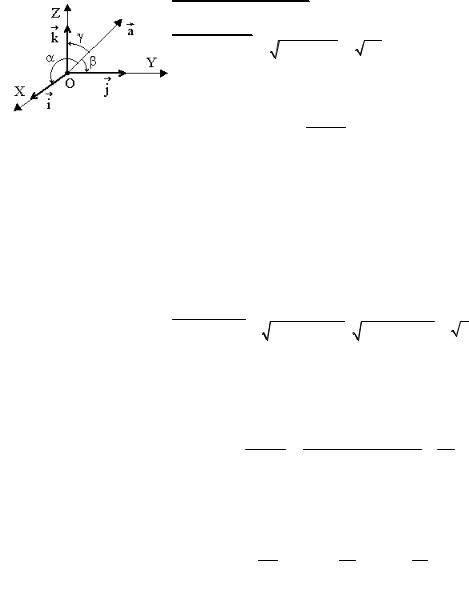
Задача 4. |
Найти |
косинусы |
углов, |
|
которые |
|
составляет |
|
|
вектор |
||||||||||||||||
ar ={ax ;ay ;az } |
с координатными осями (рисунок 17). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
• Согласно формуле (12) |
|
|
|
|
ar i |
|
ax 1 + ay |
0 + az |
0 |
|
|
|
|
|
|
|
||||||||||
|
|
r |
|
r |
r |
|
|
|
|
ax |
|
|
||||||||||||||
cosα = cos ( OX ,a ) = cos ( i ,a ) |
= |
r |
|
r |
|
|
= |
|
|
r |
|
1 |
|
= |
|
|
r |
. |
||||||||
|
|
|
|
|
|
|
a |
i |
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь учтено, что i ={1; 0; 0} и |
|
ir |
|
= 1. |
|||||||||
|
|
||||||||||||
Аналогично для других углов. Таким образом: |
|||||||||||||
cosα = |
ax |
, cos β = |
ay |
|
|
az |
|||||||
r |
|
|
r |
, cosγ = |
|
|
|
r |
. (13) |
||||
|
| a | |
|
|
a |
|
|
|
|
|
a |
|
||
Косинусы этих углов называют направляющими косинусами вектора a .
Рисунок 17
62
Заметим, что cos2 α + cos2 β + cos2 γ = 1. Это равенство доказывается непо-
средственно подстановкой выражений (13) для cosα, |
cosβ, cosγ (рекомендуется |
|||||||
проверить самостоятельно). • |
|
|
||||||
Пример 11. Единичный вектор aro имеет одинаковые острые углы с координат- |
||||||||
ными осями. Найти эти углы и координаты вектора aro . |
|
|||||||
• По условию |
|
r |
|
o |
π |
|
|
|
|
|
|
|
|||||
|
a |
|
|
= 1 и α = β = γ < 2 . Используя формулу (13), получим |
||||
|
|
|
|
|
||||
cosα = ax = ay = az |
. Поэтому 3 ax2 = 1 ax = + |
|
1 |
(знак «+» взят из-за |
||||
|
3 |
|||||||
|
|
|
|
|
|
|
|
|
того, что угол α – острый). |
|
|
||||||
Итак, α = β =γ = arccos |
1 |
≈ 36o , вектор aro = |
1 |
{1, 1, 1} . |
• |
||
|
3 |
3 |
|||||
|
|
|
|
|
|
||
Критерий перпендикулярности двух векторов a и b можно записать так: |
|||||||
r |
r |
|
r |
axbx + ayby + azbz = 0 . |
|
||
a b a |
b = 0 |
|
|||||
Пример 12. Определить, |
|
при |
каком значении |
параметра |
λ векторы |
||
ar ={2; 4; λ} и b ={λ; 3; 1} перпендикулярны.
• Найдём ar b = 2 λ + 4 3 + λ 1 = 3λ + 12 и приравняем его нулю:
3λ + 12 + 0 λ = −4. •
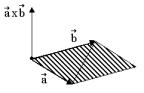
3. Вычисление работы (механический смысл скалярного произведения)ur
Пусть материальная точкаurперемещается прямолинейно вдоль вектора S под
действием постоянной силы F , направленной под углом ϕ к вектору перемеще- ur
ния S (рисунок 18).
|
|
|
|
|
|
Из механики известно, что работа, совершаемая этой |
||||||
|
|
|
|
|
силой, равна |
ur |
ur |
|
||||
|
|
|
|
|
A =| F | |
| S | cosϕ. Но это по определению |
||||||
|
|
|
|
|
|
|
|
|
|
|
uur |
ur |
|
|
|
|
|
есть скалярное произведение векторов F и |
S . Таким |
||||||
|
|
|
|
|
образом, |
|
|
|
|
|||
|
|
Рисунок 18 |
|
|
|
|
|
A = F S . |
(14) |
|||
|
Пример |
13. |
Найти |
|
работу, |
которую производит равнодействующая сил |
||||||
ur |
r |
r |
ur |
|
r |
|
|
|
|
|
|
|
F1 |
= i |
− j |
и F2 |
= 2i + j |
+ |
k |
, если её точка приложения, двигаясь прямолинейно, |
|||||
перемещается из начала координат О в точку В(2; 1; 3). |
|
|||||||||||
|
|
|
|
|
|
|
|
ur |
uur |
uur |
+ 2; −1 + 1; 0 + 1} ={3; 0; 1} . |
|
|
• Равнодействующая сила F = F1 |
+ F2 ={1 |
||||||||||
|
|
|
|
uur |
|
|
|
|
|
uur |
|
|
Вектор перемещения OB |
={2; 1; 3} . Работа A = F OB = 3 2 + 0 1 + 1 3 = 9. • |
|||||||||||
63

2.2 Векторное произведение векторов
Векторным |
произведением двух векторов a и b называется вектор cr , та- |
||||||
кой что: |
|
|
r |
|
r |
||
1) |
r |
|
= |
r |
r |
||
c |
|
a |
b |
sin ( a |
,b ) ; |
||
2)cr ar и cr b ;
3)тройка векторов a , b , c – правая тройка векторов, т.е. вращение вектора
a к вектору b на меньший угол происходит против часовой стрелки, если смотреть с конца вектора c .
Обозначение векторного произведения: ar×b .
2.2.1 Основные свойства векторного произведения
Свойство 1. |
ar×br = − (br×ar) , т.е. при перестановке сомножителей вектор- |
||||
ное произведение изменяет направление. |
|
|
|||
Свойство 2. |
r |
r |
r |
r |
r |
a |
×( λb ) = ( λa )×b |
= λ( a |
×b ) , т.е. числовой множитель |
||
можно выносить за знак векторного произведения.
Свойство 3. |
|
r |
r |
r |
|
|
|
a ×b = 0 |
a || b . Это свойство можно использовать как кри- |
||||
терий коллинеарности двух векторов. В частности, a ×ar = 0 . |
||||||
. Свойство 4. |
i ×rj = kr, |
rj × kr = ir, |
kr× ir = rj . |
|||
Свойство 5. |
r |
r |
r |
r |
r |
r |
a |
× ( b + c ) = a |
× b + a |
× c , т.е. векторное произведение обла- |
|||
дает распределительным свойством.
Свойства 1 – 4 легко получить из определения векторного произведения. Это рекомендуется проделать читателю самостоятельно. Свойство 5 доказывается более сложным образом и в данном пособии это доказательство не приводится.
Пример 14. |
Вычислить ar×b , если |
|
|
|
||||
r |
r r |
r |
r |
r |
= 1, |
r |
= 2, |
r r |
a |
= m − n, b = 2m |
+ n, |
m |
n |
( m ,n ) = 30o. |
|||
• Найдём вначале ar×br = ( mr − nr ) ×( 2mr +
тем, что m × mr = nr × nr = ar× br = 3 mr × nr = 3 mr
nr ) = 2mr × mr + mr × nr − 2nr×mr − nr× nr . Воспользуемся 0, nr × mr = −mr × nr . Отсюда следует, что
nr sin ( mr ,nr ) = 3 1 2 sin 30o = 3 . •
64
2.2.2 Вычисление векторного произведения в координатной форме
|
Пусть ar ={ax ;ay ;az }, |
br ={bx ;by ;bz }. Вычислим ar×b , воспользовав- |
|||||||||||||||||||
шись свойствами векторного произведения: |
|
|
|
|
|
|
|||||||||||||||
r |
r |
|
r |
|
r |
|
r |
|
r |
|
r |
|
|
r |
|
|
|
r r |
r r |
r r |
+ |
a |
×b |
=( axi |
+ay j |
+azk ) ×( bxi |
+by j |
+bzk ) =axbxi ×i + axbyi ×j |
+axbzi ×k |
||||||||||||||
|
|
+ aybx rj ×ir+ayby rj ×rj +aybz rj ×kr+azbxkr×ir+azbykr×rj +azbzkr×kr = |
|
||||||||||||||||||
|
|
=axbykr−axbz rj −aybxkr+aybzir+azbx rj −azbyir = |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
r |
|
|
|
r |
|
|
|
|
r |
|
|
|
||
|
|
=( aybz −azby )i −( axbz |
−azbx ) j +( axby −aybx )k |
= |
|
|
|||||||||||||||
|
|
|
ay az |
|
|
a |
a |
|
ax |
ay |
|
|
ir rj kr |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
= |
|
r |
r |
r |
= |
. |
|
|
|
||||||||||
|
|
|
|
i − |
|
x z |
j + |
|
|
k |
a |
x |
a |
a |
|
|
|
|
|||
|
|
|
by bz |
|
|
bx bz |
|
bx |
by |
|
|
|
|
y z |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
bx |
by bz |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, получена легко запоминающаяся формула вычисления вектор-
ного произведения в координатах:
r |
r |
|
|
ir |
rj |
kr |
|
. |
(15) |
|
|
||||||||
= |
|
a x |
a y |
a z |
|
||||
a |
× b |
|
|
||||||
|
|
|
|
bx |
b y |
bz |
|
|
|
В последних действиях использовано правило вычисления определителей второго порядка и разложение определителя третьего порядка по элементам первой строки.
Пример 15. Вычислить векторное произведение векторов ar ={1; 2; 0} и b = ir − rj + kr.
|
r |
r |
|
|
i |
rj kr |
|
|
r |
|
2 0 |
|
|
|
r |
|
1 0 |
|
|
r |
|
|
1 2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
• |
a × b |
= |
|
1 2 0 |
|
= i |
|
−1 1 |
− |
j |
|
1 1 |
|
|
+ k |
|
|
1 −1 |
|
|
= |
|||||||
|
|
|
= |
|
1 −1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2i − rj − 3kr ={2; −1; − 3} . • |
|
|
|
|
|
|
|
|||||||||||||||||
|
2.2.3 |
Приложения векторного произведения |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1. Вычисление площади параллелограмма и тре- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
угольника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Известно, |
|
|
что |
|
площадь |
параллелограмма |
||||||||||||
|
|
|
|
|
|
|
|
|
S=a b sinϕ. Если сравнить эту формулу с первым |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
пунктом определения векторного произведения |
|||||||||||||||||||
|
Рисунок 19 |
|
|
r |
r |
|
= |
r |
|
|
r |
|
|
|
r |
r |
|
|
|
|
|
|
||||||
|
|
|
a |
× b |
|
a |
b |
sin ( a ,b ) , то можно сделать вывод, что |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65
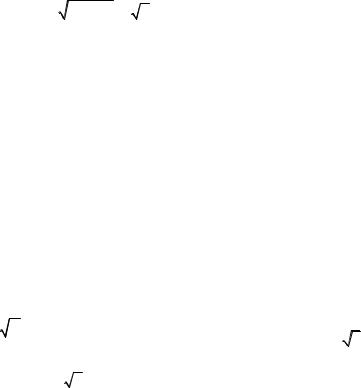
модуль векторного произведения даёт площадь Sпар. параллелограмма, построен-
ного на векторах a и b как на сторонах (рисунок 19): |
|
|||||
Sпар. = |
|
r |
r |
|
|
(16) |
|
|
|||||
|
a |
× b |
|
. |
||
В этом заключается геометрический смысл векторного произведенияr . r Очевидно, что площадь треугольника, построенного на векторах a и b , равна
|
1 |
|
r |
r |
|
|
||
|
|
|
||||||
Sтр. = |
|
|
|
a |
× b |
|
. |
|
2 |
||||||||
|
|
|
|
|
|
|
||
Пример 16. Найти площадь ∆ABC , если А(1; –1; 2), В(0; 1; 1), С(–1; 3; 1). |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uur |
uuur |
||
• Можно считать, что ∆ABC построен на векторах AB и AC . Найдём коор- |
|||||||||||||||||||||||||||
динаты этих векторов: |
|
|
|
|
|
|
|
|
|
uuur |
|
|
|
|
|
|
|
||||||||||
uur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
AB = |
{0–1; 1–(–1); 1–2}={–1; 2; |
–1},rACr |
= {–1–1; 3–(–1); 1–2}={–2; 4; –1}. |
||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
uuur |
|
|
uuuur |
|
1 |
|
|
i |
j k |
|
1 |
|
r |
r |
r |
|
|||
Тогда: |
S∆ABC |
= |
|
|
AB |
× AC |
= |
|
| |
−1 |
2 − 1 |
| = |
|
|
i 2 |
− j |
( −1 ) + k 0 |
= |
|||||||||
2 |
2 |
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
4 − 1 |
|
|
|
|
|
|
||||||
|
= |
1 |
|
|
{2, 1, 0} |
|
= |
22 + 12 |
|
= |
5 |
. |
• |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. Нахождение вектора, который одновременно перпендикулярен двум заданным векторам a и b
В качестве такого вектора n можно взять вектор ar×b (согласно второму пункту определения векторного произведения).
Пример 17. Найти единичный вектор |
r |
|
|
|
|
|
||||||||||
no , перпендикулярный плоскости тре- |
||||||||||||||||
угольника АВС, если А(1; 0; 1), |
В(1; 1; 0), С(0; 1; 1). |
|
|
|
||||||||||||
• Рассмотрим векторы |
|
|
|
|
|
uuur |
|
|
|
|
||||||
uuur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
AB =r{1–1; 1–0; 0–1}={0; 1; –1} и AC = {0–1; 1–0; 1–1}={–1; 1; 0}. |
||||||||||||||||
Вектор n , |
перпендикулярный плоскости |
∆ABC , |
можно определить как вектор, |
|||||||||||||
одновременно перпендикулярный векторам |
uur |
uuur |
|
|
|
|||||||||||
AB и AC , т.е. |
|
|
|
|||||||||||||
|
|
|
|
|
|
i |
rj |
kr |
|
|
|
|
|
|
|
|
r |
|
|
uuur |
uuuur |
r |
|
r |
r |
|
|
|
|||||
n = AB |
× AC = |
|
0 1 − 1 |
= i 1 − |
j ( −1 ) + k 1 = {1; 1; 1} . |
|
|
|||||||||
|
|
|
|
|
|
−1 1 |
0 |
|
|
|
|
|
|
|
||
|
r |
|
|
|
|
|
|
|
ro |
|
|
|
ro |
|
1 r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ясно, что |
n |
|
= |
3 . В качестве |
n |
можно взять любой из векторов n |
= ± |
|
n . |
|||||||
|
3 |
|||||||||||||||
|
|
|
|
ro |
|
1 |
{1; 1; 1}. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, n |
= ± |
|
|
• |
|
|
|
|
|
|||||||
3 |
|
|
|
|
|
|||||||||||
66
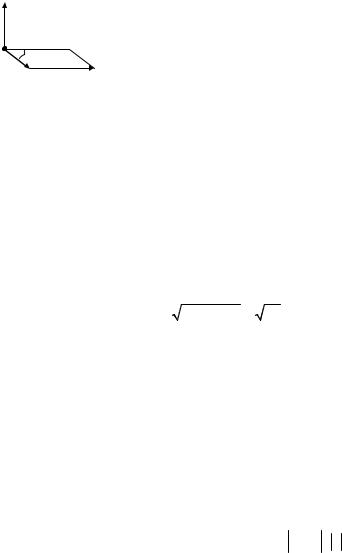
3. |
Нахождение момента сил |
|
|
|
uur |
|||||||
ur |
|
|
|
|
Из механики известно, |
что величина | M | момента |
||||||
M |
|
|
|
|
|
ur |
приложенной в точке А, относительно точки В |
|||||
|
|
|
|
силы F , |
||||||||
|
|
|
|
|
|
ur |
|
uuur |
|
|
||
В |
ϕ |
|
|
равна | F | | BA | sinϕ , где ϕuur– угол между линией дей- |
||||||||
|
|
|
|
ствия силы и направлением |
BA . Направлен момент пер- |
|||||||
|
A |
F |
|
|
|
|
|
|
|
|
|
uuur |
|
|
пендикулярно этим линиям так, что тройка векторов BA , |
||||||||||
|
Рисунок 20 |
|
ur |
ur |
|
|
|
|
||||
|
F , |
M – правая. А это означает, что |
||||||||||
|
|
|
|
|
|
|
|
|
|
uur |
r |
(17) |
|
|
|
|
|
|
|
|
|
|
M = BA× F . |
||
В этом заключается механический смысл векторного произведения. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
ur |
= i |
r |
Пример 18. Найти величину момента силы F |
+ 2 j , приложенной к точке |
|||||||||||
А(1; –2; 1), относительно начала координат О. |
|
|
||||||||||
• Момент силы |
|
ir |
rj |
kr |
|
|
|
|
|
|
||
|
uur |
uuur uur |
|
|
|
r |
r |
|
r |
|||
|
|
|
|
|||||||||
|
M |
= OA × F |
= |
1 − 2 1 |
|
= i |
( −2 ) − j ( −1 ) + k 4 ={−2, 1, 4}. |
|||||
|
|
|
|
1 |
2 |
0 |
|
|
|
|
|
|
Величина момента силы |
|
ur |
|
|
4 + 1 + 16 = |
21 . • |
||||||
| M |= |
||||||||||||
2.3 Смешанное произведение векторов
Смешанным произведением трёх векторов ar,b ,cr называется число, равное
( ar× b ) cr .
Таким образом, смешанное произведение является результатом двух операций: первые два вектора умножаются векторно, а затем полученный вектор уже скалярно умножается на третий вектор.
2.3.1 Основные свойства смешанного произведения
Свойство 1. Знак смешанного произведения определяет ориентацию тройки векторов.
Из определения скалярного произведения ( ar × br ) cr = ar× br cr cosα , где α –
угол между векторами ar× b и c . Таким образом, знак смешанного произведения
совпадает со знаком cosα . Для правой тройки векторов ar,b ,cr угол α будет острым, а для левой – тупой. Поэтому,
если ( ar |
× b ) cr > 0 , то ar,b ,cr |
– правая тройка; |
если ( ar |
× b ) cr < 0 , то ar,b ,cr |
– левая тройка. |
67
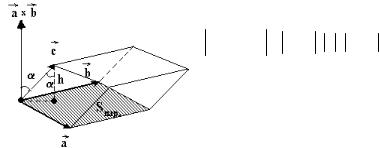
Свойство 2. Модуль смешанного произведения равен объёму Vпар. параллелепипеда, построенного на векторах ar,b ,cr (рисунок 21).
Действительно,
(ar× br) cr = ar× br cr cosα =Sпар. h=Vпар.,
т. к. | ar×b |= S пар., | c | | cosα | = h .
Рассмотренное свойство выражает геометри-
ческий смысл смешанного произведения.
Рисунок 21
Свойство 3. ( ar× b ) cr = ar ( b × cr ) = ( br× cr ) ar.
Это следует из свойств 1 и 2 (модули совпадают как объёмы одного и того же параллелепипеда, а тройки ar,b ,cr и b , cr, ar – одной ориентации).
В дальнейшем, смешанное произведение будем обозначать так: ( ar,br,cr ), не выделяя, какие два вектора перемножаются векторно.
Свойство 4.
( ar,b ,cr ) = ( br,cr,ar ) = ( cr,ar,br ) = − ( br,ar,cr ) = − ( ar,cr,br ) = − ( cr,br,ar ) .
|
|
|
|
|
|
|
|
r |
|
r |
|
|
|
r r |
r |
|
r |
|
r |
|
r |
– одной ориентации, а тройки |
|||||||||||||
Действительно, тройки a ,b ,c ; |
|
b ,c ,a ; |
c ,a ,b |
||||||||||||||||||||||||||||||||
r |
r |
|
r r |
r |
r r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b ,a ,c ; |
a ,c ,b ; |
c ,b ,a – другой ориентации. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Свойство 5. Критерий компланарности трёх векторов: |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
r |
|
r |
|
|
|
|
|
|
|
|
|
r r r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
( a , b , c ) = 0 a ,b , c – компланарные векторы. |
|||||||||||||||||||||||||||||||
Доказательство легко усматривается из второго свойства смешанного произве- |
|||||||||||||||||||||||||||||||||||
дения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.3.3 |
Вычисление смешанного произведения в координатной форме |
||||||||||||||||||||||||||||||||||
Пусть даны векторы ar ={ax ; ay ; az }, br ={bx ; by ; bz }, cr ={cx ; cy ; cz } . |
|||||||||||||||||||||||||||||||||||
Вычислим смешанное произведение в координатах: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
r |
r |
r |
r |
r |
r |
|
|
a |
y |
a |
z |
|
|
|
|
ax az |
|
|
a |
x |
a |
y |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{cx ; cy ; cz } = |
|||||||||||||||||
( a ,b ,c ) = ( a |
× b ) c |
= |
|
b b |
|
|
, − |
b b |
, |
|
b b |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
z |
|
|
|
|
x |
|
z |
|
|
|
x |
y |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
= cx |
|
ay az |
|
− cy |
|
ax az |
|
+ cz |
|
ax ay |
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
b |
b |
|
b |
x |
b |
|
|
b |
x |
b |
y |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
z |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68
Таким образом, получена удобная для запоминания формула вычисления сме-
шанного произведения в координатах:
r |
r |
r |
ax ay az |
|
|
|||
bx |
by |
bz |
. |
(18) |
||||
( a ,b ,c ) = |
||||||||
|
|
|
cx |
cy |
cz |
|
|
|
При записи формулы (18) использовано разложение определителя третьего порядка по третьей строке.
2.3.3 Приложения смешанного произведения
1. Вычисление объёмов параллелепипедов, треугольных призм и пирамид
По свойству 2, объём параллелепипеда, построенного на векторах ar, br, cr ,
равен
Vпар. = |
|
|
r r r |
|
|
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|||||||
|
( a , b , c ) |
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
|
1 |
|
r r r |
||
Очевидно, объём треугольной призмы Vпр. = |
|
|
|
Vпар. = |
|
|
| ( a ,b ,c ) | , |
||||||
2 |
|
2 |
|
||||||||||
|
1 |
|
1 |
|
|
|
1 |
|
r r r |
||||
а объём треугольной пирамиды Vпир. = |
|
|
|
Vпр. = |
|
|
Vпар. = |
|
|
|
| ( a ,b ,c )| . |
||
|
|
3 |
6 |
|
6 |
|
|||||||
Пример 19. Треугольная пирамида задана координатами вершин A(1; 2; 0),
B(0; 1; 1), |
C(1; 0; 1), |
D(1; 1; 1). Найти объём пирамиды и высоту, опущенную |
|||||||||||||||
из вершины D (рисунок 22). |
|
|
uur |
uuuur |
uuuur |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
• Пирамида построена, например, на векторах AB, AC , AD . |
|
|
|
||||||||||||||
Укажем координаты этих векторов: |
uuur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
uur |
uuuur |
|
={0; −1; 1} . |
|
|
|
|
|
|||||||||
AB ={−1; |
−1; 1} , AC |
={0; − 2; 1} , AD |
|
|
|
|
|
||||||||||
|
|
Вычислим |
|
−1 − 1 |
1 |
|
|
|
|
|
|
|
|
||||
|
|
uuur uuuur uuur |
|
|
|
|
|
−2 1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
0 |
− 2 1 |
|
= −1 |
= 1 . |
|
|||||||||
|
|
( AB , AC , AD ) = |
|
|
|||||||||||||
|
|
|
|
0 − 1 1 |
|
|
|
|
|
−1 1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рисунок 22 |
Объём пирамиды V |
|
= |
1 |
|
1 = |
1 |
. |
|
|
|
||||||
|
6 |
|
|
|
|
|
|||||||||||
|
|
|
|
пир. |
|
|
|
6 |
|
|
|
3Vпир. |
|
||||
Высоту h можно найти из соотношения: V |
= |
1 |
|
S |
|
|
|
|
h h |
= |
. |
||||||
3 |
|
|
|
|
|
S∆ABC |
|||||||||||
|
|
|
|
пир. |
|
|
|
∆ABC |
|
|
|
|
|||||
69
|
|
|
|
|
|
|
|
|
1 |
uuur |
|
|
uuuur |
|
1 |
|
|
|
i |
rj |
kr |
|
|
|
|
1 |
r |
r |
|
r |
|
|
6 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Найдём S |
|
|
|
|
= |
|
|
AB× AC |
= |
|
| |
−1 |
−1 |
1 |
|
| = |
|
|
|
i 1 − j |
( −1 )+k |
2 |
= |
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
∆ABC |
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
0 |
−2 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Итак, h = |
|
6 |
|
= |
. • |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
6 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Проверка векторов на компланарность |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Свойство 5 позволяет решать ряд важных задач. Приведём примеры. |
|
|
|
||||||||||||||||||||||||||||||||||||||
Пример 20. Проверить, являются ли векторы |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
r |
|
|
r |
|
|
|
r |
r |
|
|
|
r |
|
|
r |
|
r |
r |
|
|
|
r |
r |
компланарными? |
|
|
|
|
|
||||||||||||
a |
= i − j |
+ k , b |
|
= j |
− k , c = i |
+ j |
− k |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
r |
r |
|
r |
|
|
|
1 |
−1 |
|
|
1 |
|
|
|
1 − 1 |
|
|
|
|
|
−1 |
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
• Вычислим ( a ,b ,c ) |
= |
|
0 |
1 |
|
−1 |
|
= 1 |
1 − 1 |
|
+ |
1 |
1 |
−1 |
= 0. |
|
|
|
|
|
|||||||||||||||||||||
|
( ar,b ,cr ) = 0 , |
|
|
|
|
|
|
1 |
1 |
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Так как |
|
значит ar,b ,cr |
|
– компланарные векторы. • |
|
|
|
|
|
||||||||||||||||||||||||||||||||
Пример 21. Проверить, лежат ли в одной плоскости четыре точки A(1; 0; 1), |
|
||||||||||||||||||||||||||||||||||||||||
B(1; 1; 0), C(0; 1; 1), |
D(1; 1; 1)? |
|
|
|
|
|
uuuur |
|
|
|
|
|
|
uuur |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
• Рассмотрим векторы |
|
AB |
={0; 1; −1} , AC ={ |
−1; 1; 0} , AD ={0; 1; 0} . |
|
||||||||||||||||||||||||||||||||||||
|
uuur |
|
uuuur |
uuur |
|
|
|
0 1 −1 |
|
|
|
|
|
|
|
|
|
uur uuuur uuur |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≠ 0 , |
то рас- |
||||||||||||||||||
Вычислим ( AB, AC , AD ) = −1 1 0 = 1. Так как ( AB, AC , AD ) |
|||||||||||||||||||||||||||||||||||||||||
0 1 0
смотренные векторы некомпланарные, поэтому и точки A, B, C, D не лежат в одной плоскости. Заметим, что мы попутно вычислили объем параллелепипеда, четыре вершины которого определяются данными точками. •
3.ЗАДАЧИ
3.1Задачи с решениями
1. |
В треугольнике ABC сторону АВ точками М и N разделили на три равные |
||||||||||
части: AM = MN = NB. |
|
|
uuur |
|
|
uur |
r uuur |
r |
|||
Найти вектор CM , если CA = a , CD = b . |
|||||||||||
|
uuur |
r |
r |
uuuur |
1 uuur |
1 |
r |
r |
|
|
|
• |
Имеем AB |
= b |
−a |
AM = |
|
AB = |
|
( b |
−a ). |
|
|
3 |
3 |
|
|
||||||||
70
