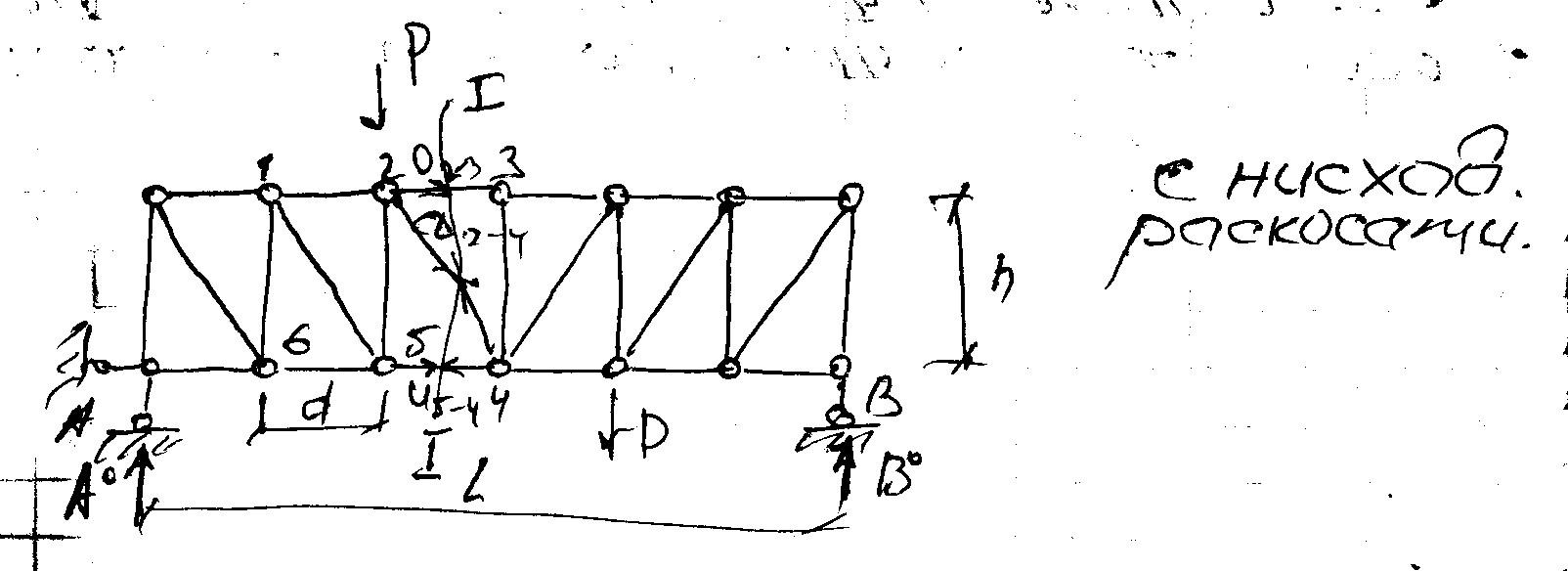
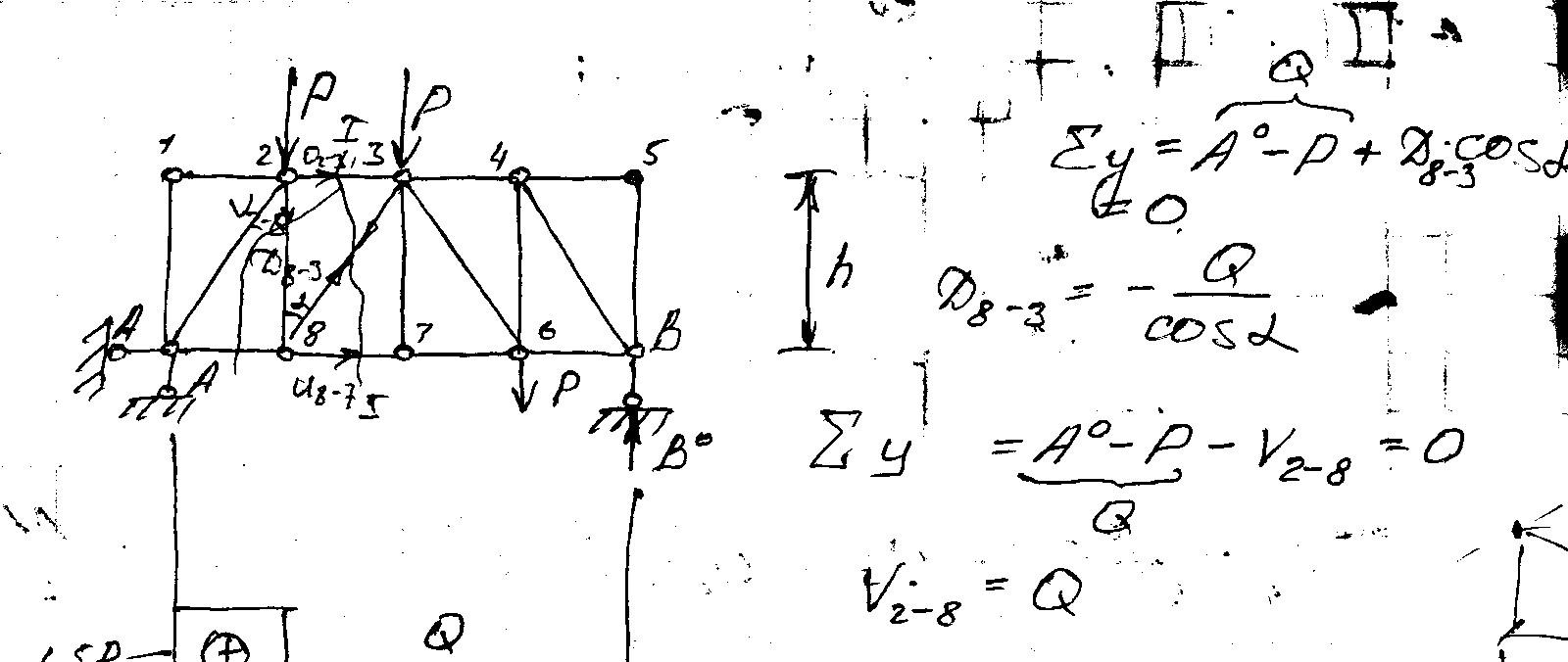
Доказательство теоремы клапейрона
Определим
работу, которую совершает сила ![]() ,
действующая, например, на балку,
изображенную на рис. 15.1, а.
,
действующая, например, на балку,
изображенную на рис. 15.1, а.
Будем
считать, что нагрузка прикладывается
к балке статически, то есть она медленно
возрастает от нуля до заданной величины![]() .
.
Пусть
в некоторый момент сила, достигшая
значения ![]() ,
вызвала в месте своего приложения прогиб
балки, равный
,
вызвала в месте своего приложения прогиб
балки, равный ![]() .
.
Увеличим
это значение силы на бесконечно малую
величину ![]() .
Такое изменение нагрузки приведет к
дополнительному прогибу
.
Такое изменение нагрузки приведет к
дополнительному прогибу ![]() .
Очевидно, что элементарная дополнительная
работа будет равна:
.
Очевидно, что элементарная дополнительная
работа будет равна: ![]() .
.
Полная
работа, совершенная внешней силой,
определяется по формуле: 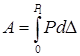 .Для
линейно деформируемой системы (график
зависимости между прогибом
.Для
линейно деформируемой системы (график
зависимости между прогибом ![]() и
силой P для такой системы показан на
рис. 15.1, б) прогиб балки пропорционален
внешней нагрузке, то есть
и
силой P для такой системы показан на
рис. 15.1, б) прогиб балки пропорционален
внешней нагрузке, то есть ![]() ,
,
где ![]() –
коэффициент пропорциональности или
перемещение от силы, равной единице
–
коэффициент пропорциональности или
перемещение от силы, равной единице ![]() .
Коэффициент
.
Коэффициент ![]() часто
называют и податливостью системы.
часто
называют и податливостью системы.
Дифференцируя
уравнение ![]() ,
найдем:
,
найдем: ![]() .
.
Подставляя
формулу ![]() в
формулу
в
формулу 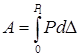 и
учитывая уравнение
и
учитывая уравнение ![]() ,
получим:
,
получим: 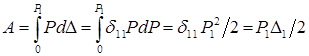 ,что
и требовалось доказать. Полученное
выражение соответствует теореме
Клапейрона.
,что
и требовалось доказать. Полученное
выражение соответствует теореме
Клапейрона.
34, Построение линий влияния в стержнях балочных ферм статическим способом.

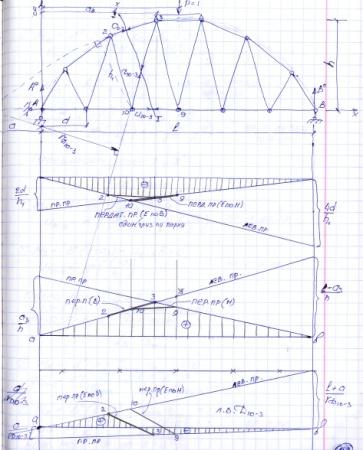

35,Сопоставление арочных и балочных ферм

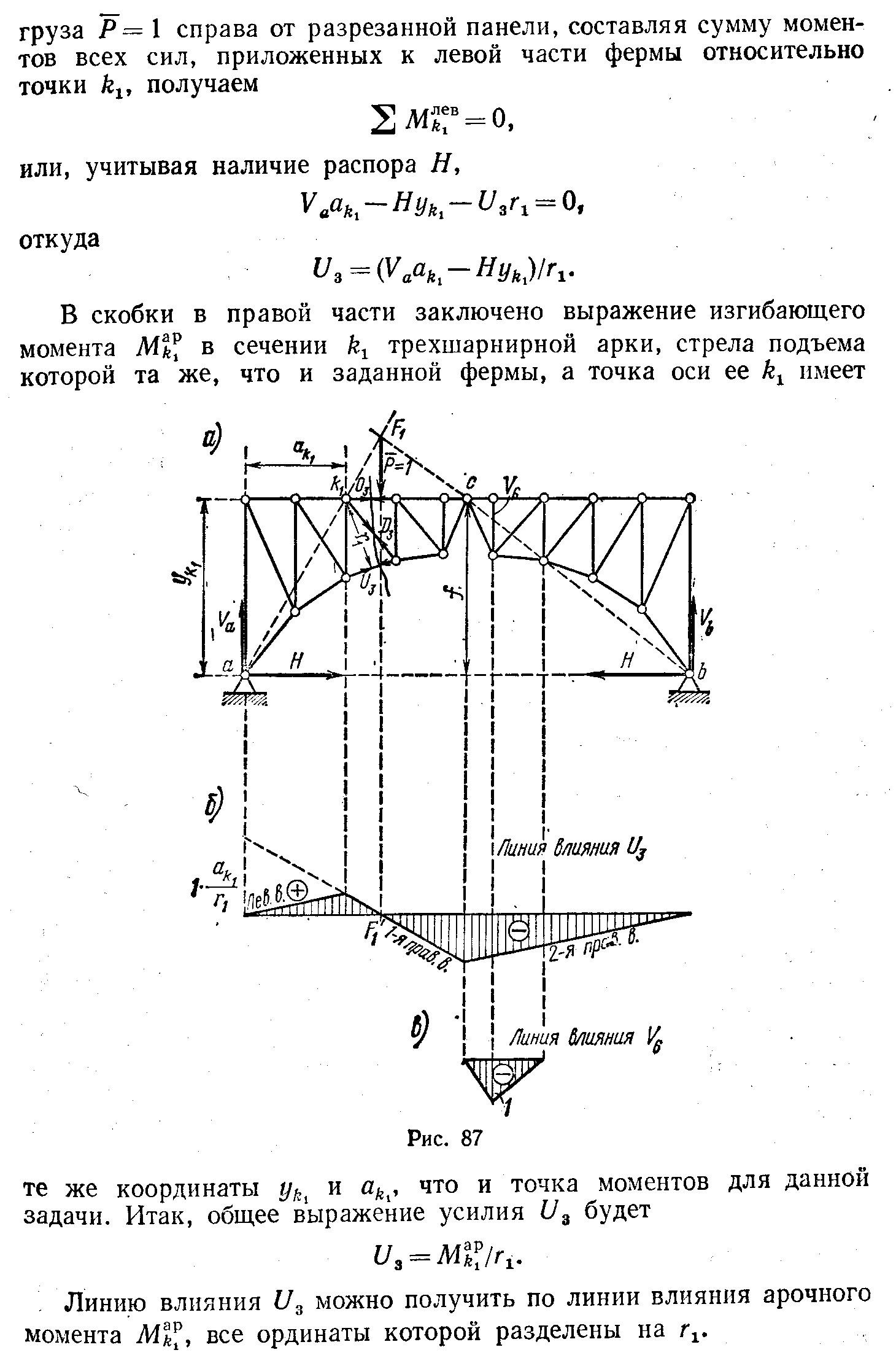
36, Свойство прямолинейного участка ЛВ.
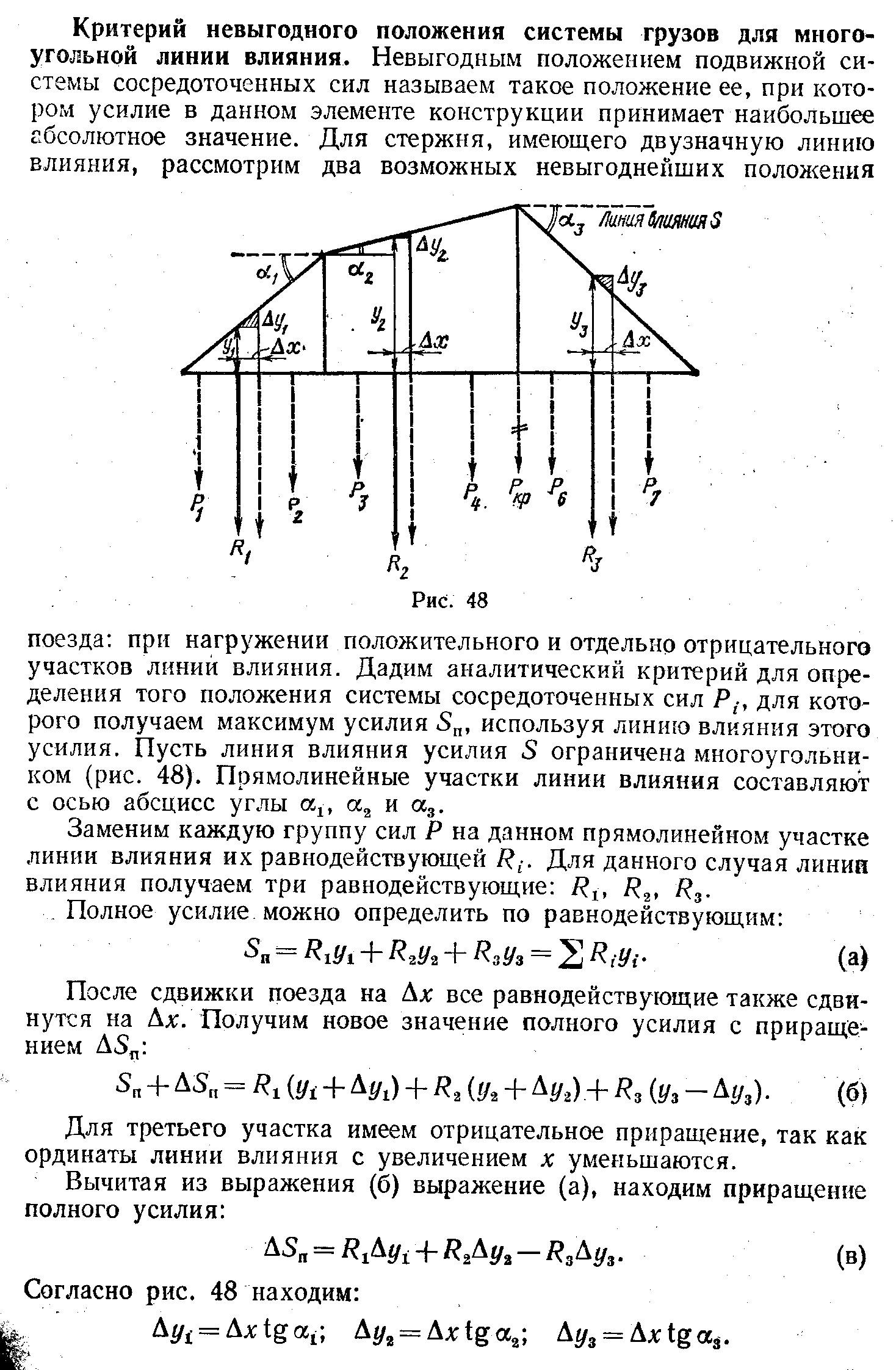
38, ЛВ М,Q опорных реакций для простых балок с консолями
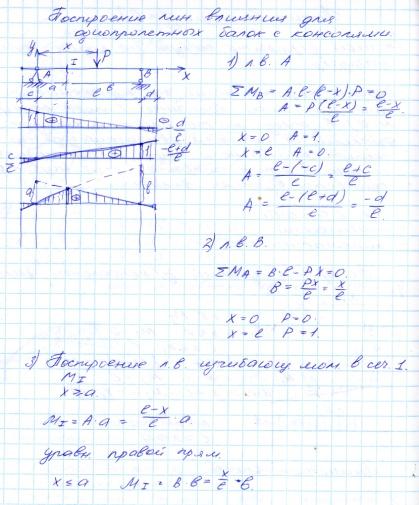
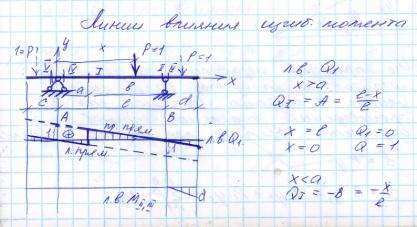
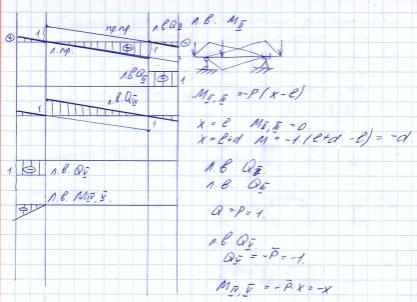
40,ЛВ балки заделанной одним концом

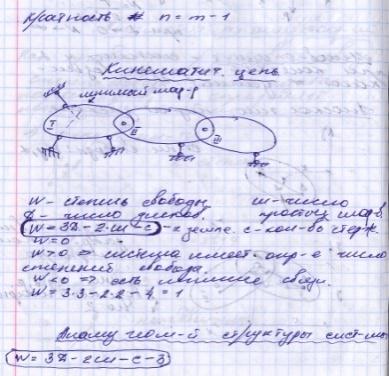
41 Способы образования плоских геометрически неизменяемых систем.
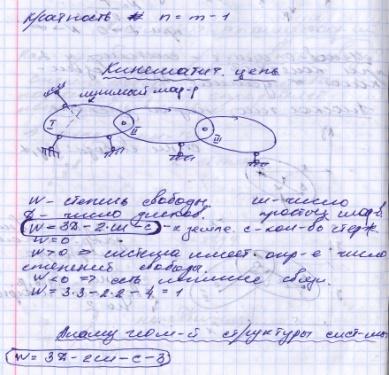
43.Определение усилий в стрежнях ферм.
Для любой статически определимой фермы можно составить 2К уравнений статики (К – число узлов фермы), с помощью которых можно найти опорные реакции и внутренние усилия в ее стержнях от действия внешней нагрузки. При этом в первую очередь обычно определяют опорные реакции. При определении реакций составляют 3 уравнения равновесия для всей фермы в целом.
Для определений внутренних усилий следует выделять сечениями узлы или отдельные части фермы и рассматривать условия их равновесия под действием внешних нагрузок и усилий в рассеченных стержнях. Всего можно составить 2К – 3 таких условий.
Выделение узлов или частей фермы необходимо производить так, чтобы усилия в элементах фермы определялись наиболее просто.
Метод моментной точки. Применяется в тех случаях, когда удается рассечь ферму на две части так, чтобы при этом перерезанными оказались три ее стрежня, направления осей которых не пересекаются в одной точке. Направления осей трех таких перерезанных стержней пересекаются попарно в трех точках, не лежащих на одной прямой. Составляем последовательно уравнения моментов всех сил, действующих на отсеченную часть фермы, относительно этих трех точек, каждый раз будем получать уравнение с одним неизвестным, представляющим собой усилие в рассеченном стержне.
1 разрезаем ферму так, чтобы в разрез кроме данного стержня попали еще 2 других (оси которых не сходятся с ним в одной точке)
2 из уравнения моментов относительно точки пересечения осей этих 2 стержней определяем усилие в данном стержне
При составлении уравнений равновесия все неизвестные усилия в стержне условно считаются положительными, т.е. растягивающими и направленными от узлов. Если после решения уравнений какое – либо усилие окажется отрицательным, значит, оно является сжимающим и направленно к узлу. При расчетах ферм способом моментной точки каждое усилие определяется с помощью одного уравнения с одним неизвестным.
Способ проекций. Применяется в следующих двух вариантах:
1 рассматривается равновесие части фермы (как и при способе моментной точки), когда два из трех рассеченных стержней параллельны друг другу
2 рассматривается равновесие выделяемых из фермы узлов (способ вырезания узлов).
При расчете простейших ферм все усилия можно определить способом проекций, применяя его последовательно к каждому узлу. При этом определение усилий надо считать с узла, в котором сходиться не более двух стержней.
При расчете ферм способом вырезания узлов усилия в ряде стержней можно найти только после предварительного определения усилий в других стержнях. В связи с этим случайная ошибка в определении одного усилия может привести к неправильному определению усилий в целом ряде стержней.
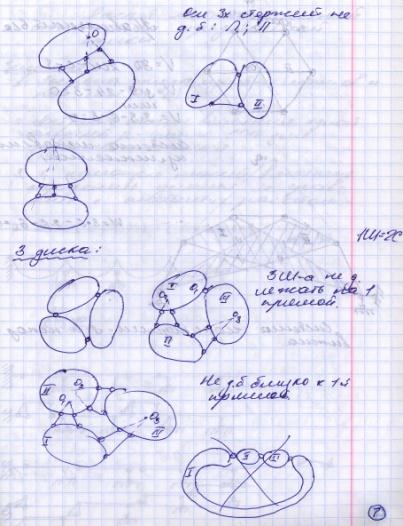
44, Примеры анализа геометрической структуры сооружения
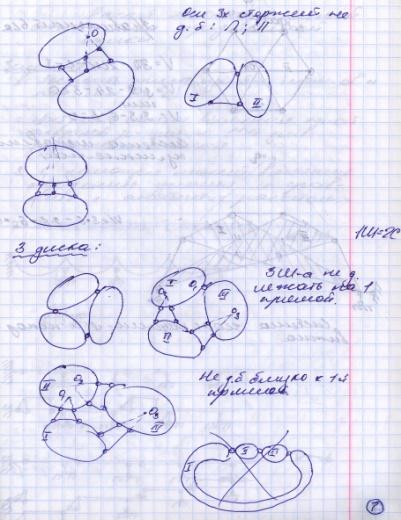
45 Образование и расчет шпренгельных ферм



46,Зависимость усилий в Эл-х фермы от очертания поясов и решетки.