1.4.3. Линии влияния поперечной силы

Величина и знак поперечной силы зависят от положения единичного груза относительно сечения к, и поэтому будем строить линию влияния поперечной силы при двух предположениях, как и

для изгибающего момента.

Пусть единичный груз движется справа от сечения

QK = A = ( l – x ) / l .

Это выражение поперечной силы определяет правую ветвь линии влияния. В этом случае поперечная сила положительная, так как стремится повернуть балку по часовой стрелке ( слева – вверх ).

При x = 0 Q = 1 ,

при x = l Q = 0 .

Во втором случае, когда груз движется слева от сечения, выражение поперечной силы будет

QK = – B = – x / l ,

которое определяет левую ветвь. Поперечная сила отрицательная, так как стремится повернуть балку против часовой стрелки ( справа –вверх ).

При x = 0 Q = 0 ,

при x = l Q = – 1 .

Линия влияния поперечной силы приведена на рис. 1.4, в.

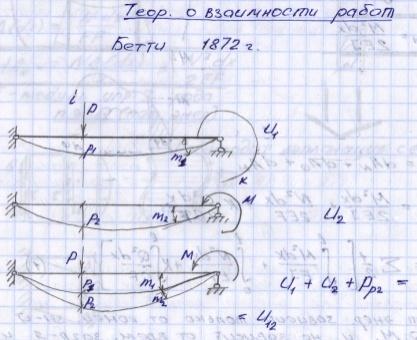
20,Теорема о взаимности работ

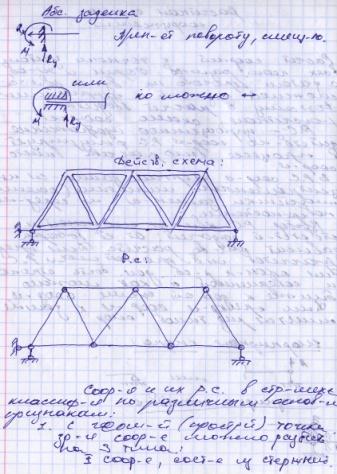
21 Способы образования и условия геометрической неизменяемости плоских ферм.

22,Расчетная схема. Осн. Элементы и их РС.

23. Формула Мора

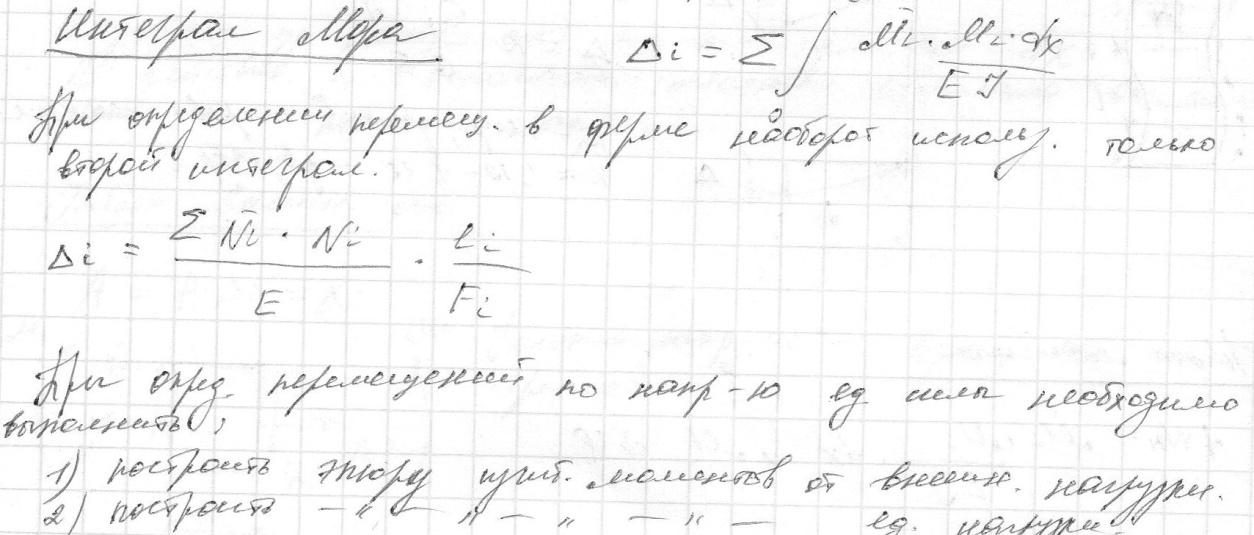
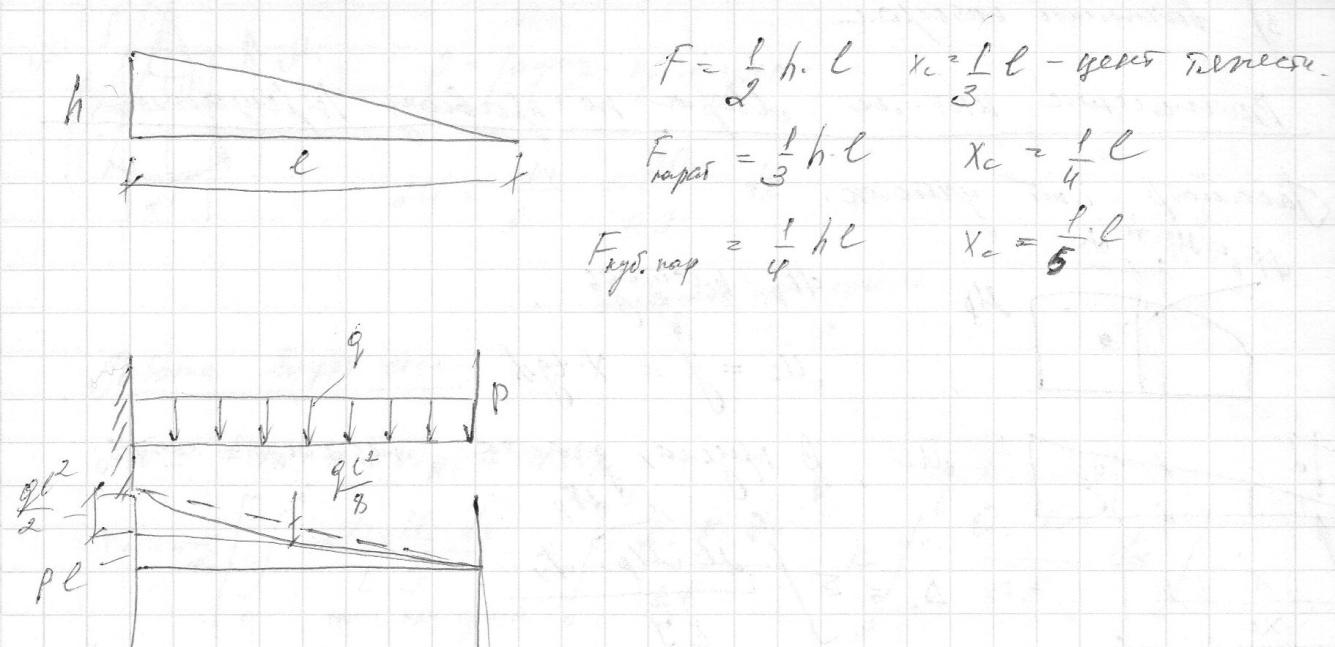
25. Частные случаи равновесия узлов ферм.

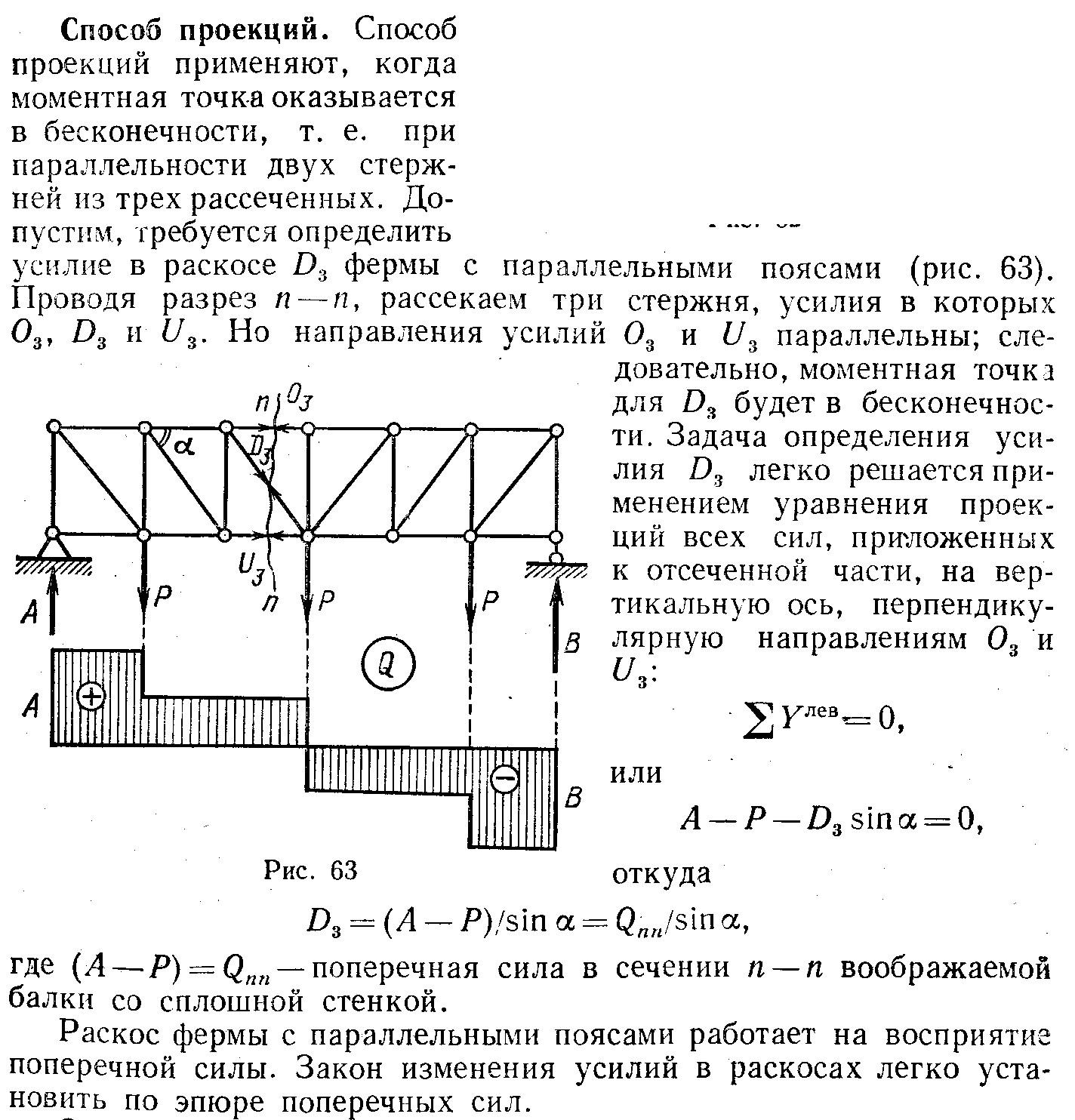
26 Определение усилий в стержнях фермы (способ проекций)

27,Невыгоднейшее загружение треугольной ЛВ

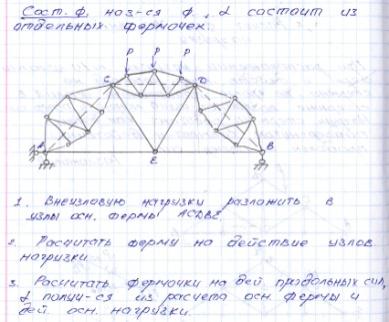
28 Расчет составных ферм

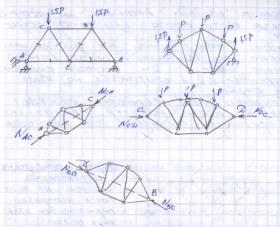
29, ЛВ усилий при узловой передаче нагрузки

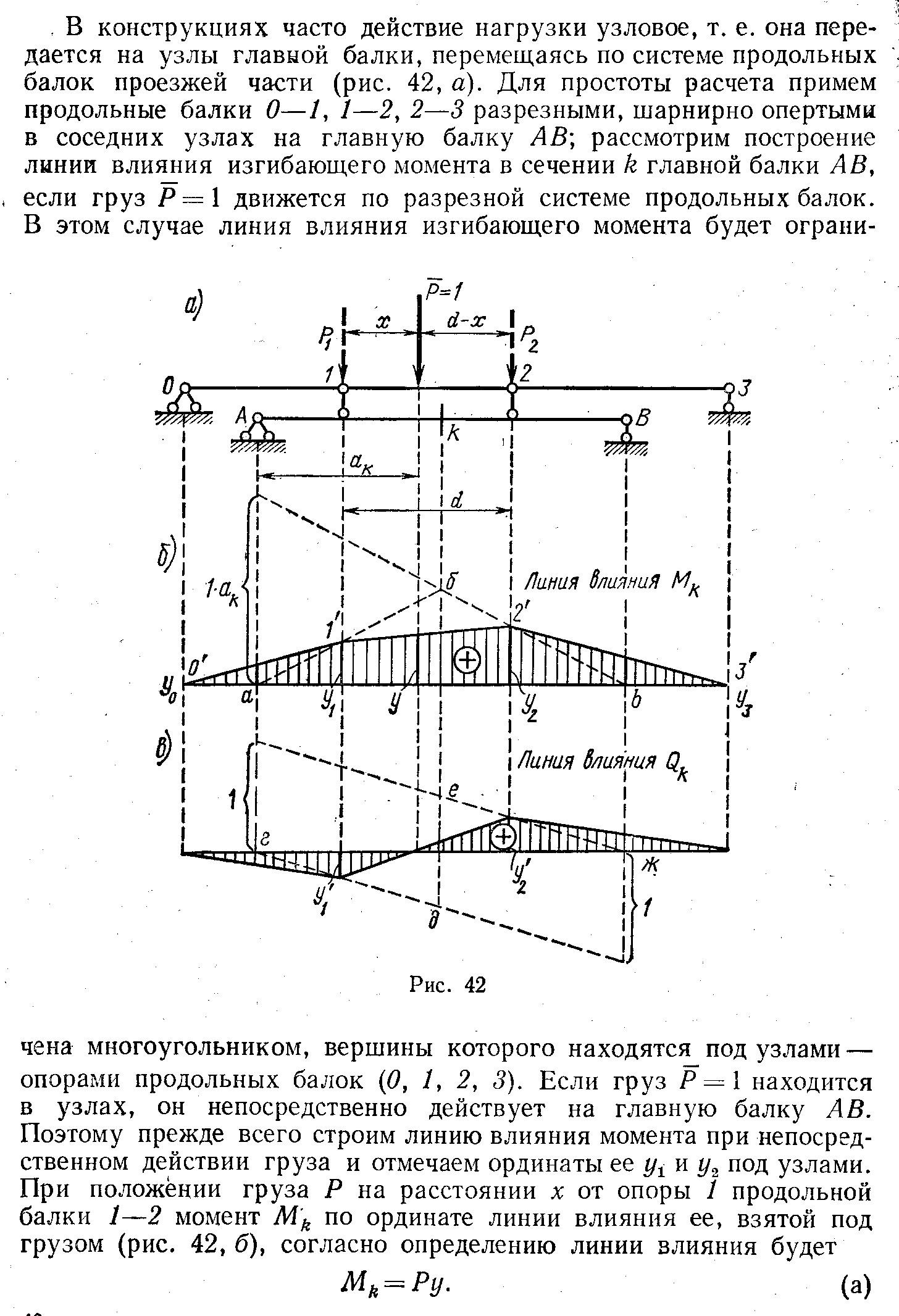
31,Потенциальная энергия системы

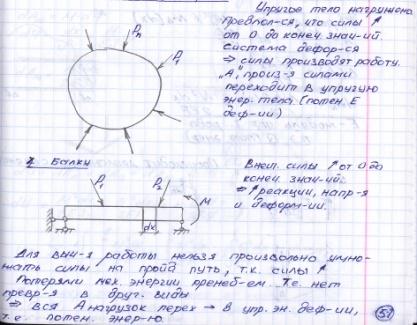
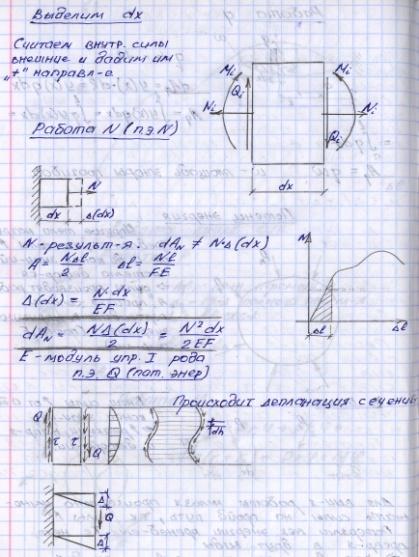
32 Применение уравнений 3-х моментов для расчёта неразрезных балок.

В качестве основной системы необходимо взять систему разрезных балок, полученную из заданной системы включением шарниров в опорные сечения. За неизвестное примем опорный изгиб. Моменты, очевидно, что число их равно числу промежуточных опор при наличии крайних шарнирных опор. Решение выбранной основной системы заключается в том, что эпюры моментов от единичных усилий распространяются в ней только на два соседних пролёта и значит, большое число побочных перемещений обращается в ноль. Для составления типового канонического уравнения в развёрнутом виде строим эпюры изгибающих моментов в основной системе от внешней нагрузки и единичных усилий. Из рассмотрения этих эпюр вытекает, что типовые канонические уравнения будет трёхчлен следующего вида:

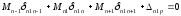
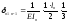
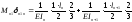
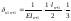
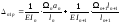
Подставляем: ……

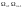- площади эпюр моментов;

a_n , b_n+1 – расстояние от центров тяжести этих эпюр. Умножим правую и левую части на 6EI_c получаем:

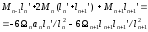
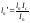
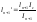
Уравнение 3-х моментов в общем виде. Если I=const

В уравнениях неизвестными являются 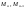т.е. для расчёта неразрезной балки необходимо составить столько уравнений трёх моментов, сколько промежуточных опор, решая совместно внешним силам.

Если конец защемлён, для применения уравнения трёх моментов вводим дополнитьельный фиктивный пролёт. Для опоры ‘o’ составляем уравнения:

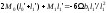
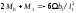
При отсутствии внешней нагрузки на крайнем 1-м пролёте у защемлённого конца:

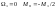
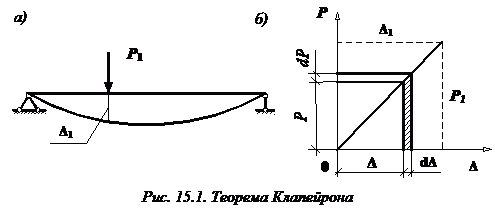
33,Теорема Клапейрона

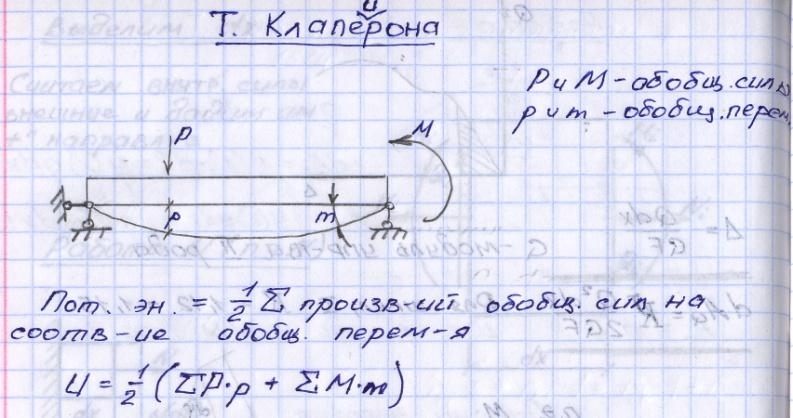
Формулировка теоремы Клапейрона: упругая работа внешней силы при статическом приложении равна половине произведения ее окончательного значения на соответствующее этой силе перемещение.

Теорема Клапейрона впервые была сформулирована французским ученым Клапейроном в 1852 г.