1.9. Механика жидкостей и газов

1. Давление жидкости на дно и стенки сосуда:

,

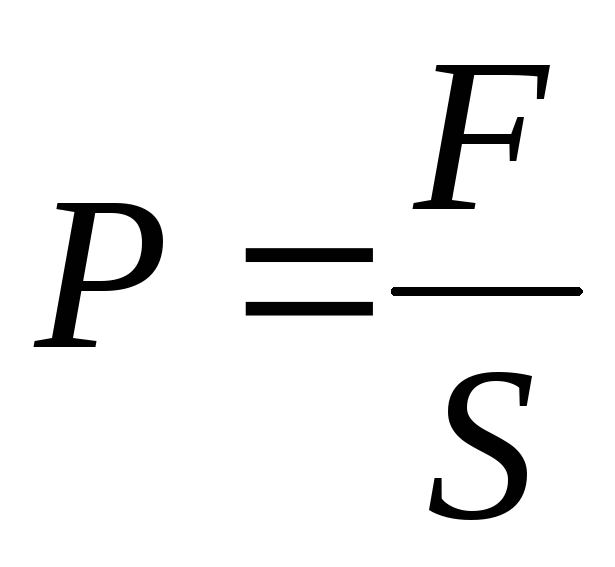где F – сила, действующая на поверхность S.

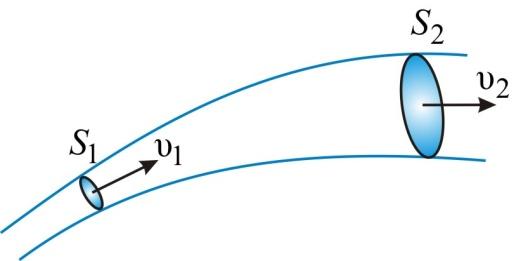
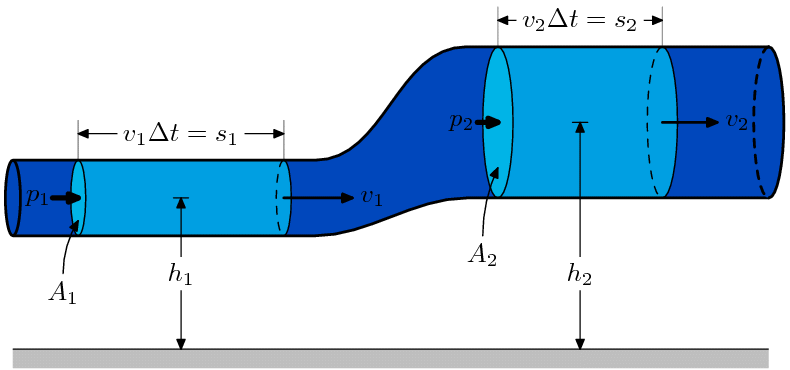
2. Уравнение неразрывности для несжимаемой жидкости (рис. 1.55, 1.56):

Рис. 1.55	Рис. 1.56

3. Уравнение Бернулли:

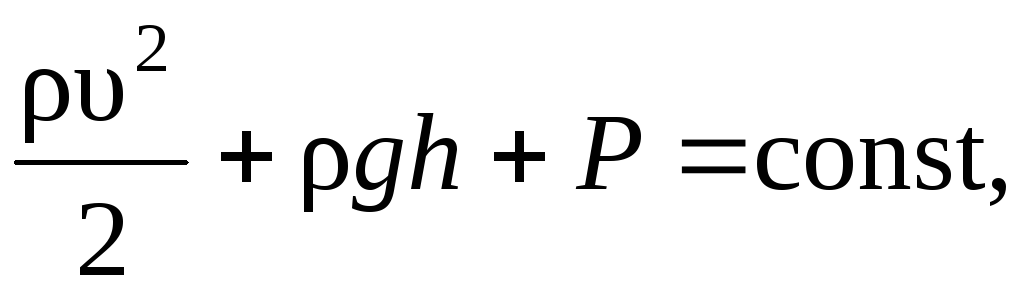
где плотность жидкости; h – высота, на которой расположено сечение; Р – статическое давление жидкости для определенного сечения трубки тока.

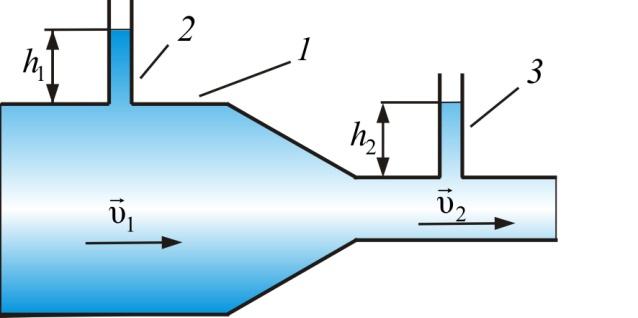
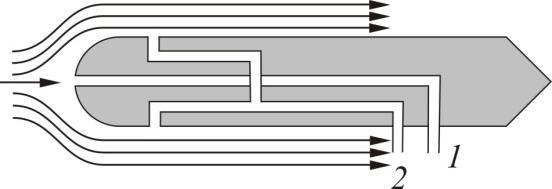
В качестве примеров применения уравнения Бернулли можно привести установку для измерения скорости течения жидкости (рис. 1.57), или устройство для измерения скорости самолета – трубку Пито (рис. 1.58).

Рис. 1.57	Рис. 1.58

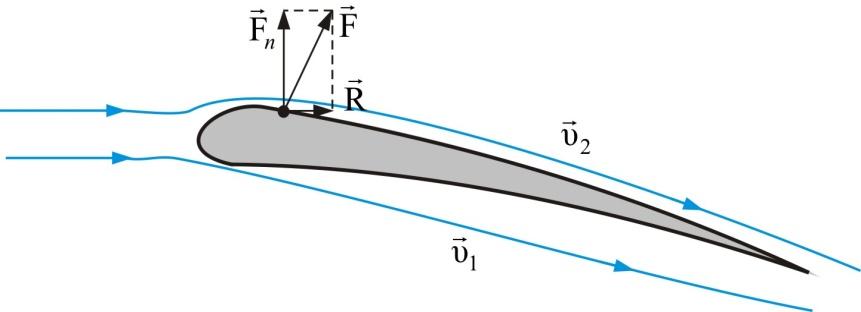
4. Подъемная сила крыла самолета: профиль крыла самолета (рис. 1.59) имеет такую форму, что скорость обтекающего потока воздуха относительно крыла внизу меньше, а вверху больше: υ₂ > υ₁. Поэтому давление над крылом меньше, чем под крылом: Р₁ > Р₂. Это приводит к избыточной силе , которую можно разложить на две составляющие: подъемную силу_п и силу сопротивления

Рис. 1.59

5. Закон сообщающихся сосудов: в сообщающихся сосудах уровни однородных жидкостей, считая от наиболее близкой к поверхности земли точки (рис. 1.60), равны:

.

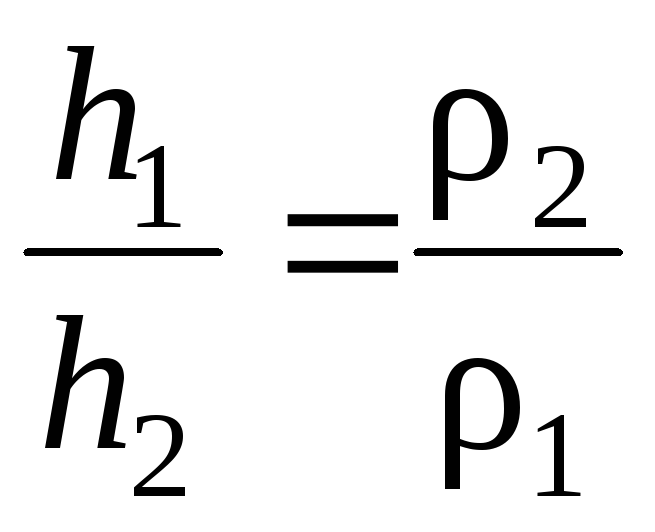6. Давление столба жидкости на глубине h:

.

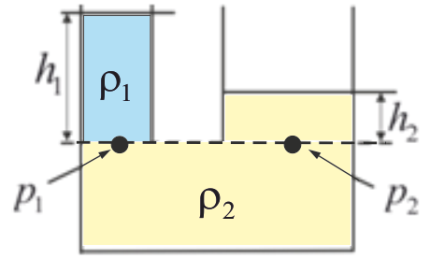
В сообщающихся сосудах, заполненных разнородными жидкостями с плотностью , давления жидкостей на одном уровне одинаковы (рис. 1.60):

.

Рис. 1.60

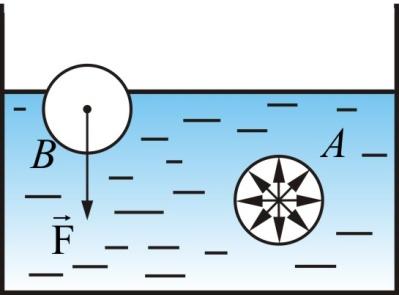
7. Закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной телом жидкости:

,

где F_A – выталкивающая сила; V – объем вытесненной жидкости.

8. Формула Торричелли, позволяющая определить скорость ис­течения жидкости из малого отверстия в открытом широком сосуде:

,

где h – глубина, на которой находится отверстие относительно

уровня жидкости в сосуде.

9. Формула Стокса, позволяющая определить силу сопротивления, действующую на медленно движущийся в вязкой среде шарик:

,

где r – радиус шарика; – скорость шарика; коэффициент вязкости.

10. Формула Пуазейля, позволяющая определить объем жидкости, протекающий за время t через капиллярную трубку длиной l:

,

где R – радиус трубки; – разность давлений на концах трубки.

11. Поверхностное натяжение (рис. 1.61):

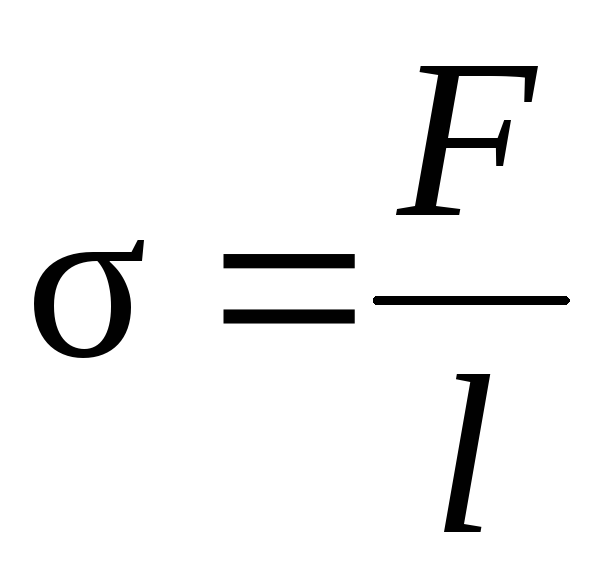или ,

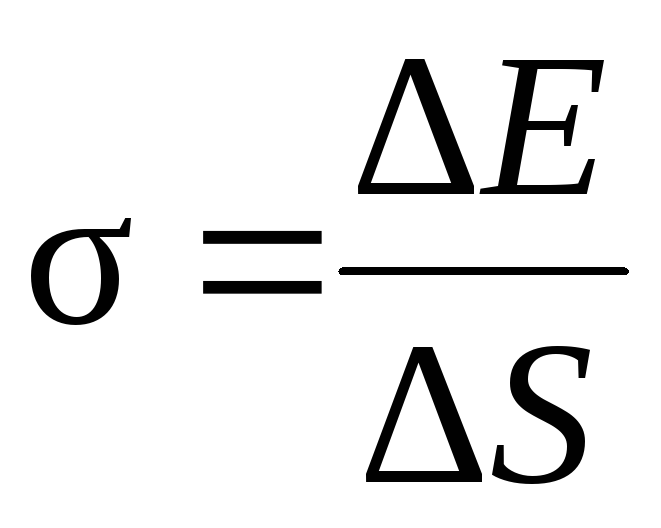где F – сила поверхностного натяжения, действующая на контур, ограничивающий поверхность жидкости; – поверхностная энергия, связанная с площадью поверхности пленки; l – длина контура, ограничивающего поверхностный слой жидкости.

12. Формула Лапласа, позволяющая определить избыточное давление для произвольной поверхности жидкости двоякой кривизны:

,

где и – радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости; радиус кривизны положителен, если центр кривизны находится внутри жидкости (выпуклый мениск), и отрицателен (рис. 1.56), если центр кривизны вне жидкости (вогнутый мениск). Для сферической поверхности:

_.

Рис. 1.61	Рис. 1.62

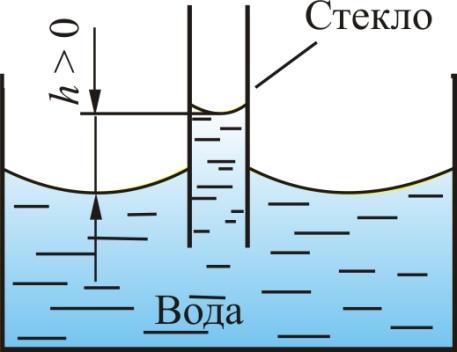
13. Высота подъема жидкости в капиллярной трубке (рис.1.61):

,

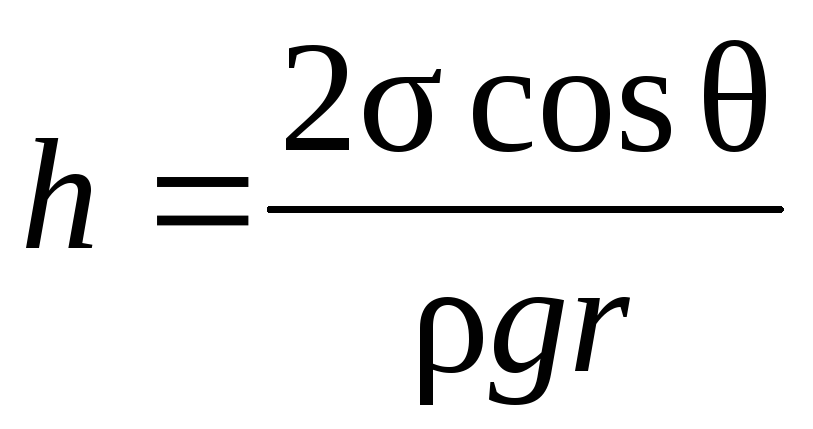где – краевой угол; r – радиус капилляра; – плотность жидкости.

14. Насыщенный пар – пар, находящийся в термодинамическом равновесии со своей жидкостью. Скорость преобразования пара равна скорости конденсации.

Давление насыщенного пара при данной температуре – максимальное давление, которое может иметь пар над жидкостью при этой температуре.

Давление насыщенного пара не зависит от жидкости объема сосуда, в котором находится пар. При изотермическом уменьшении объема насыщенного пара, часть пара переходит в жидкость, давление насыщенного пара при этом не меняется.

15. Относительная влажность воздуха – процентное отношение плотности (парциального давления) водяного пара в воздухе к плотности (парциальному давлению) насыщенного пара при той же температуре: φ = ρ/ρ(н) ∙ 100% или φ = p/p(н) ∙ 100%,

где ρ, ρ(н) – абсолютная влажность ненасыщенного и насыщенного водяного пара; p,p(н) – парциальное давление ненасыщенного и насыщенного водяного пара соответственно.

16. Абсолютная влажность воздуха – величина, равная плотности ρ водяного пара в воздухе или равная парциальному давлению P водяного пара:

или ,

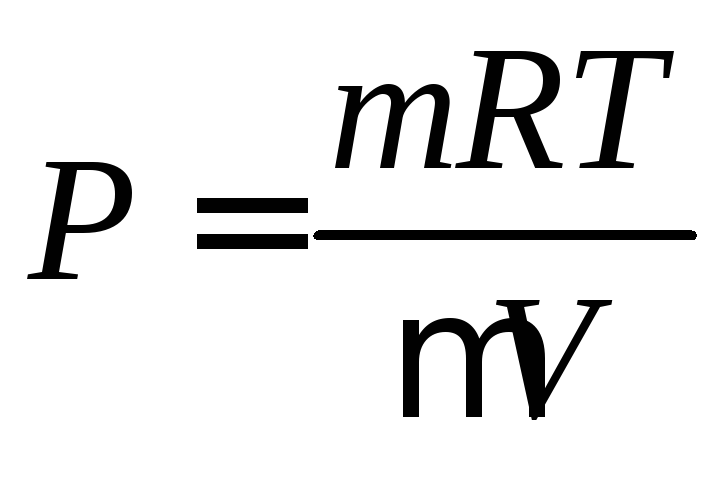где ρ – абсолютная влажность (плотность) водяного пара, m – масса водяного пара в объеме V, µ – молярная масса воды, P – парциальное давление водяного пара.

17. Точка росы – температура, при достижении которой ненасыщенный водяной пар становится насыщенным в результате изохорического охлаждения.