§ 2. Центр тяжести твёрдого тела.

С большой степенью точности можно принимать силы тяжести различных частиц твёрдого тела за параллельные, а общую силу тяжести тела считать приложенной в центре этих параллельных сил (рис.33).

В данном случае центр параллельных

сил тяжести становится центром тяжести.

Центром тяжести твёрдого тела

называется неизменно связанная с этим

телом точка, через которую проходит

л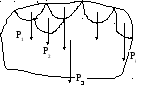иния действия равнодействующей сил

тяжести при любом положении тела в

пространстве.

Координаты центра тяжести тела относительно

Рис.33.

выбранного начала координат определяются полученными выше выражениями:

X_c=; Y_c=; Z _c=

Выражения  P_i*X _i ;  P_i*Y_i и  P_i*Z _i называются статическими моментами сил тяжести относительно координатных осей.

Примечание: Для однородных тел: силы тяжести его частей и всего тела пропорциональны длинам l, если тела составлены из тонких стержней, площадям S,

если составлены из плоских фигур и объёмам V, если тела составлены из объёмных частей.

Так что, при вычислении координат центра тяжести тел можно пользоваться формулами типа:

X_c=или X _c=или X _c=

При практических вычислениях координат центра тяжести тел можно пользоваться следующими очевидными рекомендациями:

1.Если однородное тело имеет ось симметрии, то центр тяжести лежит на этой оси.

2.Если однородное тело имеет плоскость симметрии, то центр тяжести лежит в этой плоскости.

3.Если однородное тело имеет центр симметрии, то центр тяжести совпадает с этим центром.

4.Если тело неоднородно по весу или имеет сложную конфигурацию, то его следует условно разделить на ряд частей, для которых веса и положение центров тяжести известны, а затем воспользоваться полученными выше формулами.

5.Если у тела или фигуры имеются полости, вырезы, отверстия, то для определения координат центра тяжести пользуются теми же приёмами и формулами, считая при этом веса, объёмы или площади вырезанных частей отрицательными.

Пример: Определить координаты центра тяжести плоской фигуры, изображённой на рисунке(рис.34).

Решение:

1.Расчленяем фигуру на три

участка и определяем их площади:

S₁=6*3=18

S₂=3*3=9

S₃=1*1=1

S_=S₁+S₂-S₃=26

Рис.34.

2.Определяем координаты центров тяжести частей фигуры(по рисунку)

X₁=1,5м X₂=4,5м X₃=4,5м

Y₁=3м Y₂=1,5м Y₃=1,5м

3.Вычисляем координаты центра тяжести всей фигуры

X_c=м

Y_c=м

§ 3. Равновесие при наличии трения.

В статических задачах в ряде случаев равновесие тел осуществляется при участии сил трения. Различают трение скольжения и трение качения.

а) Трение скольжения.

Силой трения скольжения называется сила сопротивления, возникающая при стремлении двигать одно тело по поверхности другого.

Установлено, что сила трения скольжения направлена в сторону, обратную предполагаемому перемещению. Сила трения пропорциональна силе нормального давления N и при отсутствии взаимной деформации не зависит от площади соприкосновения. Сила трения скольжения зависит от физической природы соприкасающихся поверхностей, качества их обработки, наличия смазки и пр.

Эти факторы учитываются коэффициентом трения скольжения f, величина которого определяется опытным путём и приводится в справочной литературе.

Например, при отсутствии смазки:

дерево по дереву f=0,40,7

металл по металлу f=0,150,25

металл по льду f=0,020,03

Силу трения скольжения принято вычислять по формуле Кулона

F_тр=f*N

б) Трение качения.

Трением качения называется сила сопротивления, возникающая при стремлении перекатывать одно тело по поверхности другого.

Рассмотрим способ вычисления силы трения качения

при стремлении катить упругое колесо по твёрдой

поверхности. Вследствие упругой деформации колеса,

образуется линия контакта АВ протяжённостью 2* (рис.35).

П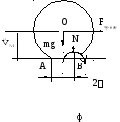опытка перекатить колесо относительно,

например, точки в силой F_{тр.кач.,}, которая воспринимается

как сила сопротивления, связана с преодолением момента,

Рис.35.

создаваемого силой тяжести. Приближённо можно записать для момента начала перекатывания

F_тр.кач.* rmg* или

F_тр.кач.mg*

Величину ,равную половине длины линии контакта колеса и поверхности качения называют коэффициентом трения качения.

Пример: К валу приложена пара сил с моментом М=100Нм.С какой силой Q надо прижимать тормозные колодки, чтобы вал

оставался в покое, если коэффициент трения

между валом и колодками f=0,25; r=0,25 м .

Рис.36.

Решение:

Силы сжатия Q, действуя через колодки на вал,

порождают силы нормального давления,

так что N=- Q. Между колодками и валом

образуются силы трения F_тр=f*N=f*Q.

Пара сил, создаваемая силами трения, должна

уравновесить момент заданной пары сил. Так что F_тр * 2 * r = M или f * Q * 2 * r = M

Следовательно Q=