§ 2.Пара сил и её свойства.

Парой сил называют систему двух равных по модулю, параллельных и направленных в противоположные стороны сил, линии действия которых не совпадают.

П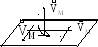ара сил характеризуется:

-плоскостью пары

-модулем сил, составляющих пару сил

-расстоянием между линиями действия сил

(плечом пары).

Рис. 11

Естественно, что пара сил не находится в равновесии. Её механическое действие сводится к повороту тела в плоскости пары

М=F*h

Момент пары рассматривают как вектор и направляют его перпендикулярно плоскости пары.

Пара сил обладает рядом свойств. Рассмотрим важнейшие из них:

Основное свойство пары (теорема1):

Сумма моментов сил пары относительно любого полюса равна моменту пары.

И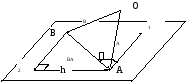з рис.13 имеем:

По определению пары

F₂=-F₁

Представим

Рис.13 Теперь найдём искомую сумму моментов:

где М = F * h – момент пары.

Таким образом, если сумма моментов сил пары не изменяется при изменении центра приведения О и остаётся равной моменту пары, то эффективность пары не изменится:

а) при переносе пары сил в любое другое место её плоскости (рис.14,а);

б) при переносе пары сил в любую другую параллельную плоскость (рис.14,б);

в) при повороте пары сил в плоскости пары на любой угол (рис.14,в).

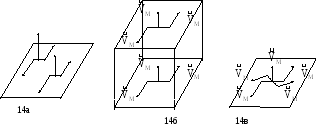
Рис.14.

Следует также отметить вполне очевидное свойство пары: две пары с одинаковыми моментами эквивалентны (оказывают на тело одинаковое действие)

M=F₁*h₁=F₂*h₂

Рассмотренные свойства пары сил позволяют сделать следующий вывод:

вектор момента пары сил М является свободным вектором.

Если на тело действует несколько пар сил, то пара сил момент которой равен сумме моментов пар сил, эквивалентна данной системе пар сил.

Приведём моменты пар к

общему плечу h и представим

М₁=F₁*h

M₂=F₂*h

M₃=-F₃*h

Таким образом

M₁+M₂+M₃=(F₁+F₂-F₃)*h=R*h=M_гл.

Рис.15

Примечание: сказанное справедливо и для случая, когда слагаемые векторы пар сил действуют в пересекающихся плоскостях (рис.16.).

Используя свойства пары, совместим векторы пар в точке О на линии пересечения плоскостей пар и найдём векторную сумму моментов пар сил:

Рис.16.

Итак, действие системы пар сил на тело эквивалентно одной паре, вектор момента которой равен сумме векторов моментов слагаемых пар. Если модуль этого суммарного вектора момента окажется равным нулю, то это эквивалентно отсутствию пары. Это обстоятельство позволяет сформулировать условия равновесия тела при действии на него системы пар сил:

Рассмотрим пример: Определить опорные реакции двухопорной невесомой балки, нагруженной двумя парами сил (Рис.17).

Дано: F₁; F₂; h₁; h₂; l_o.

Учитывая, что действие

пар можно уравновесить

только парой сил реакции,

освободимся от связей,

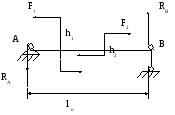положими составим

уравнение равновесия балки:

R_B=R_A=(F₁*h₁-F₂*h₂)/ l₀.

M₁=F₁*h₁ M₂=F₂*h₂