FNP

13. По заданным приближенным значениям аргументов функции и их предельным абсолютным погрешностям вычислить абсолютную и относительную (в процентах) погрешности значения функции; найти приближенное значение , сохраняя только верные цифры. ; .

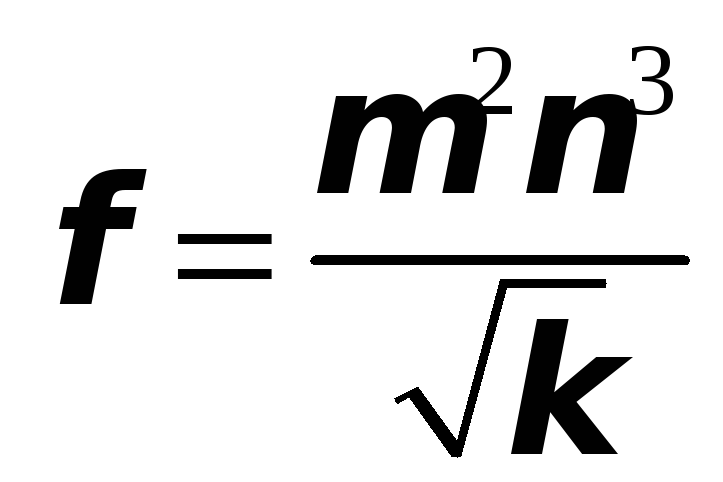ТИПОВОЙ РАСЧЕТ

по теме “Функции нескольких переменных”

Вариант №20

1. Найти и изобразить в декартовой системе координат область определения функции:

а) ; б) ;

2. Для заданной функции найти все частные производные первого порядка:

а) ; б) ;

3. Для заданной функции найти требуемые частные и смешанные производные:

;

4. Проверить, что функция удовлетворяет заданному уравнению:

;

5. Найти производные неявно заданной функции: а) ; б)

1. ; 2.

6. Найти градиент функции в точке и вычислить его модуль

;

7. Для функции в точке 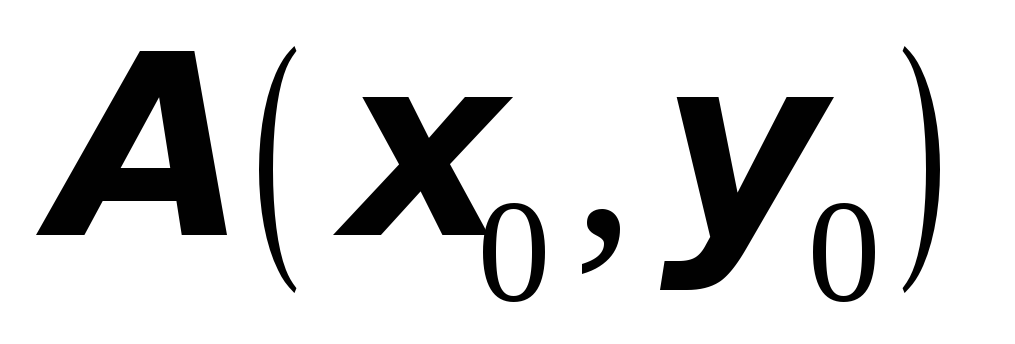вычислить градиент и производную в направлении вектора

8. Найти полный дифференциал функции:

а) ; б)

9. С помощью полного дифференциала найти приближенное значение функции:

при

10. Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке : ;

11. Исследовать на экстремум функцию ,

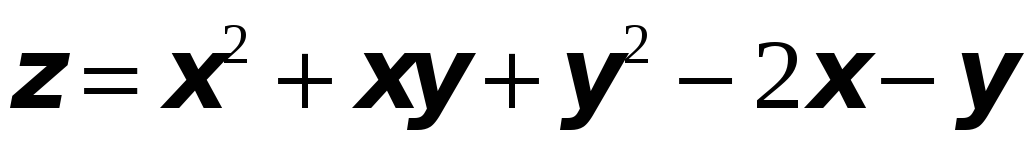
12. Известно, что в электрической цепи с сопротивлением R ток величины I в единицу времени выделяет количество тепла, пропорциональное . Как следует разветвить ток I на токи при помощи трех параллельных приводов с заданными сопротивлениями 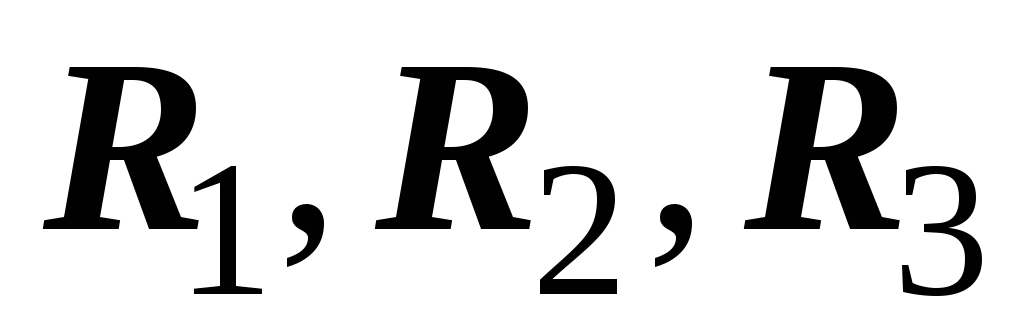, чтобы суммарное выделение тепла было наименьшим?

13. По заданным приближенным значениям аргументов функции и их предельным абсолютным погрешностям вычислить абсолютную и относительную (в процентах) погрешности значения функции; найти приближенное значение , сохраняя только верные цифры. ; .

ТИПОВОЙ РАСЧЕТ

по теме “Функции нескольких переменных”

Вариант №21

1. Найти и изобразить в декартовой системе координат область определения функции:

а) ; б) ;

2. Для заданной функции найти все частные производные первого порядка:

а) ; б) ;

3. Для заданной функции найти требуемые частные и смешанные производные:

;

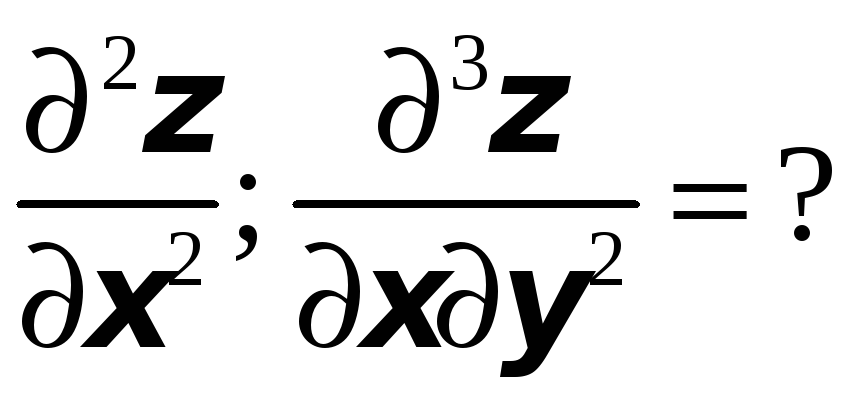
4. Проверить, что функция удовлетворяет заданному уравнению:

;

5. Найти производные неявно заданной функции: а) 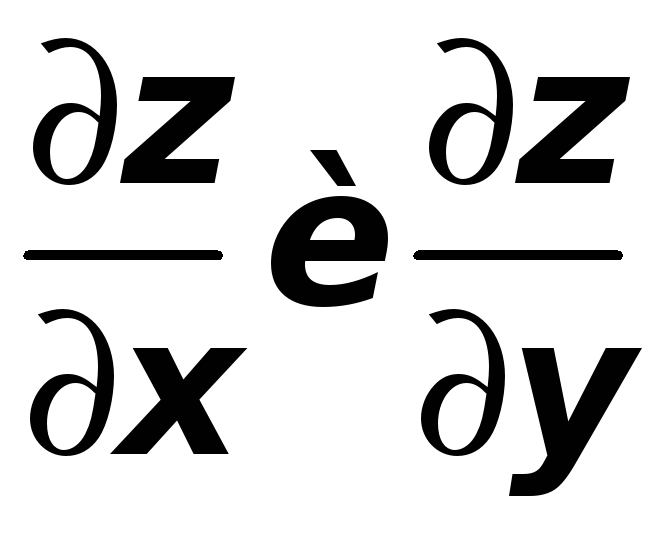; б)

1. ; 2.

6. Найти градиент функции 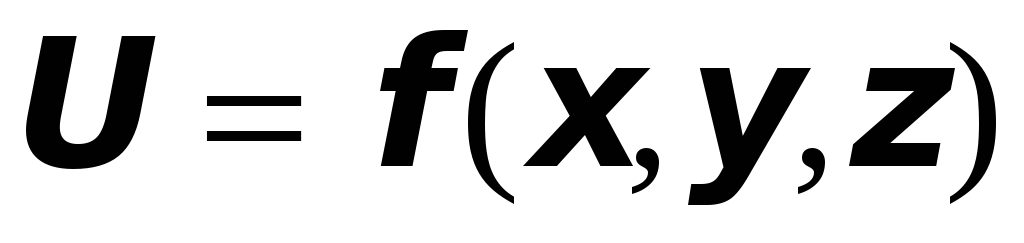в точке и вычислить его модуль

;

7. Для функции в точке вычислить градиент и производную в направлении вектора

8. Найти полный дифференциал функции:

а) ; б)

9. С помощью полного дифференциала найти приближенное значение функции:

при

10. Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке : ;

11. Исследовать на экстремум функцию ,

12. Найти размеры a, b, c прямоугольного параллелепипеда наибольшего объема, вписанного в конус с радиусом основания R и высотой H.

13. По заданным приближенным значениям аргументов функции и их предельным абсолютным погрешностям вычислить абсолютную и относительную (в процентах) погрешности значения функции; найти приближенное значение , сохраняя только верные цифры. ; .

ТИПОВОЙ РАСЧЕТ

по теме “Функции нескольких переменных”

Вариант №22

1. Найти и изобразить в декартовой системе координат область определения функции:

а) ; б) ;

2. Для заданной функции найти все частные производные первого порядка:

а) ; б) ;

3. Для заданной функции найти требуемые частные и смешанные производные:

;

4. Проверить, что функция удовлетворяет заданному уравнению:

;

5. Найти производные неявно заданной функции: а) ; б)

1. ; 2.

6. Найти градиент функции в точке и вычислить его модуль

;

7. Для функции в точке вычислить градиент и производную в направлении вектора

8. Найти полный дифференциал функции:

а) ; б)

9. С помощью полного дифференциала найти приближенное значение функции:

при

10. Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке : ;

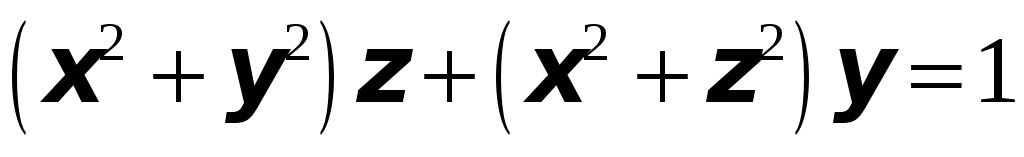11. Исследовать на экстремум функцию ,

12. Среди всех треугольников, вписанных в круг радиуса R, найти тот, площадь которого наибольшая. Определить величины a, b, c такого треугольника.

13. По заданным приближенным значениям аргументов функции и их предельным абсолютным погрешностям вычислить абсолютную и относительную (в процентах) погрешности значения функции; найти приближенное значение , сохраняя только верные цифры.

.

ТИПОВОЙ РАСЧЕТ

по теме “Функции нескольких переменных”

Вариант №23

1. Найти и изобразить в декартовой системе координат область определения функции:

а) ; б) ;

2. Для заданной функции найти все частные производные первого порядка:

а) ; б) ;

3. Для заданной функции найти требуемые частные и смешанные производные:

;

4. Проверить, что функция 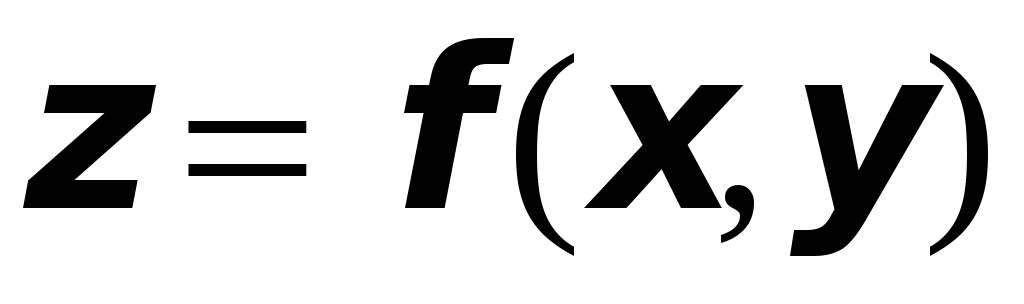удовлетворяет заданному уравнению:

;

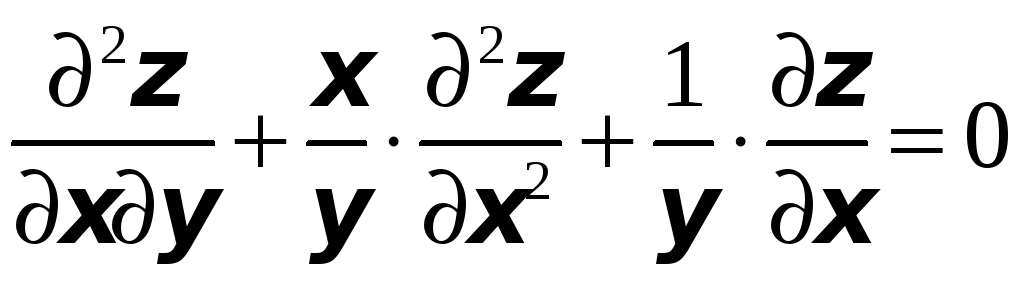
5. Найти производные неявно заданной функции: а) ; б)

1. ; 2.

6. Найти градиент функции в точке и вычислить его модуль

;

7. Для функции в точке вычислить градиент и производную в направлении вектора

8. Найти полный дифференциал функции:

а) ; б)

9. С помощью полного дифференциала найти приближенное значение функции:

при

10. Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке : ;

11. Исследовать на экстремум функцию ,

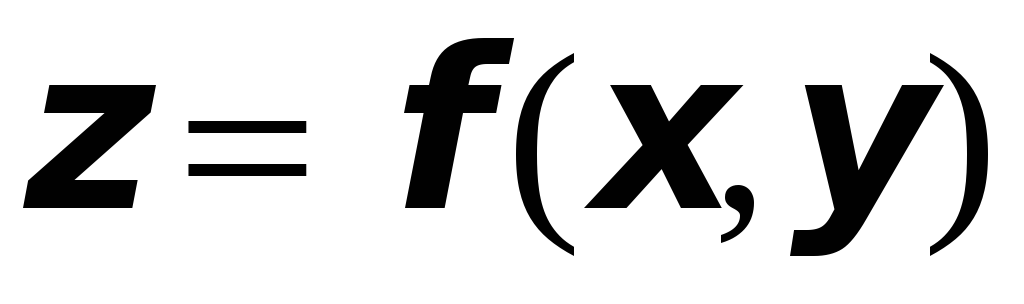12. Определить размеры m, n, p прямоугольного параллелепипеда наибольшего объема, вписанного в эллипсоид .

13. По заданным приближенным значениям аргументов функции и их предельным абсолютным погрешностям вычислить абсолютную и относительную (в процентах) погрешности значения функции; найти приближенное значение , сохраняя только верные цифры.

.

ТИПОВОЙ РАСЧЕТ

по теме “Функции нескольких переменных”

Вариант №24

1. Найти и изобразить в декартовой системе координат область определения функции:

а) ; б) ;

2. Для заданной функции найти все частные производные первого порядка:

а) ; б) ;

3. Для заданной функции найти требуемые частные и смешанные производные:

;

4. Проверить, что функция удовлетворяет заданному уравнению:

;

5. Найти производные неявно заданной функции: а) ; б)

1. ; 2.

6. Найти градиент функции в точке и вычислить его модуль

;

7. Для функции в точке 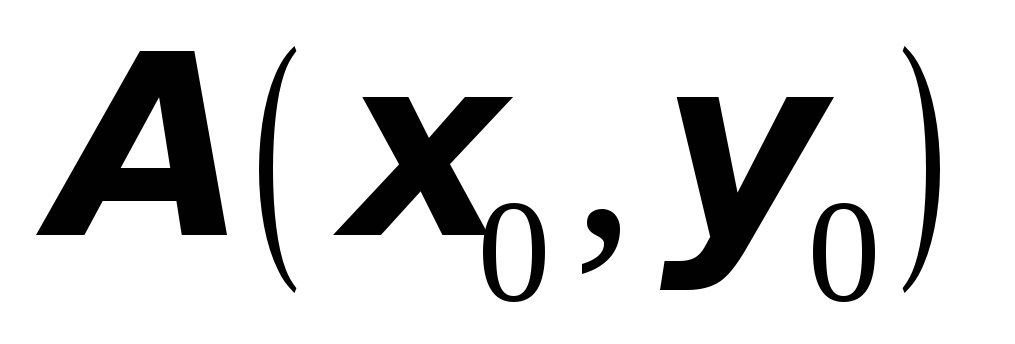вычислить градиент и производную в направлении вектора

8. Найти полный дифференциал функции:

а) ; б)

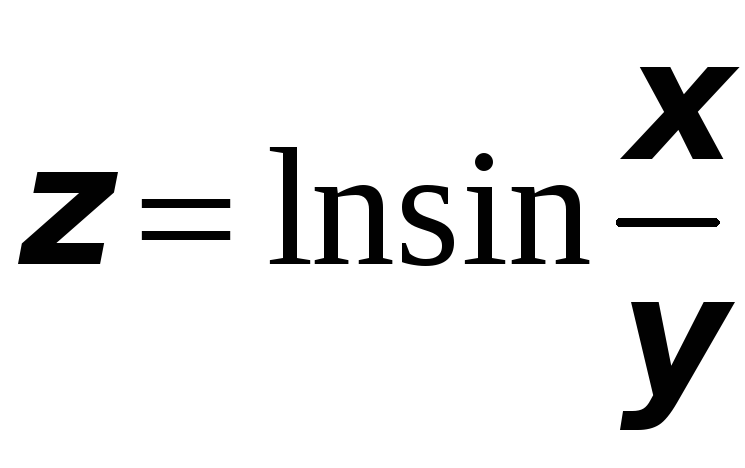
9. С помощью полного дифференциала найти приближенное значение функции:

при

10. Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке : ;

11. Исследовать на экстремум функцию ,

12. На сфере 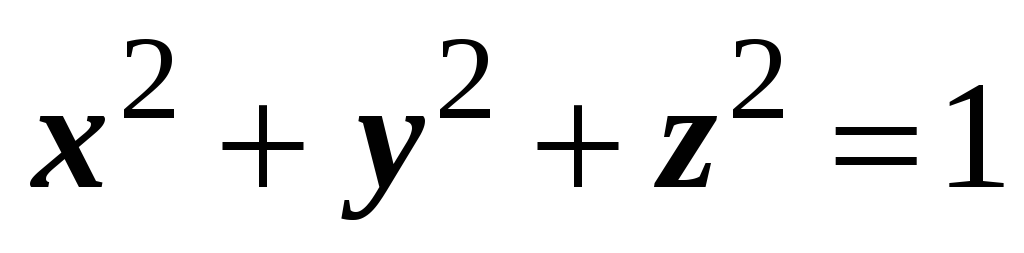найти точку , сумма квадратов расстояний которой от n данных точек является минимальной.

13. По заданным приближенным значениям аргументов функции и их предельным абсолютным погрешностям вычислить абсолютную и относительную (в процентах) погрешности значения функции; найти приближенное значение , сохраняя только верные цифры. ;

.

ТИПОВОЙ РАСЧЕТ

по теме “Функции нескольких переменных”

Вариант №25

1. Найти и изобразить в декартовой системе координат область определения функции:

а) ; б) ;

2. Для заданной функции найти все частные производные первого порядка:

а) ; б) ;

3. Для заданной функции найти требуемые частные и смешанные производные:

;

4. Проверить, что функция удовлетворяет заданному уравнению:

;

5. Найти производные неявно заданной функции: а) ; б)

1. ; 2.

6. Найти градиент функции в точке и вычислить его модуль

;

7. Для функции в точке вычислить градиент и производную в направлении вектора

8. Найти полный дифференциал функции:

а) ; б)

9. С помощью полного дифференциала найти приближенное значение функции:

при

10. Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке : ;

11. Исследовать на экстремум функцию ,

12. Тело с объемом V должно представлять собой прямоугольный параллелепипед, нижнее и верхнее основания которого завершаются одинаковыми правильными четырехугольными пирамидами. При каком угле наклона боковых граней пирамид к их основаниям полная поверхность тела будет минимальной?

13. По заданным приближенным значениям аргументов функции и их предельным абсолютным погрешностям вычислить абсолютную и относительную (в процентах) погрешности значения функции; найти приближенное значение , сохраняя только верные цифры.

.