
FNP
.doc

-
Найти полный дифференциал функции:
а)
![]() ;
б)
;
б)

-
С помощью полного дифференциала найти приближенное значение функции:
![]() при
при
![]()
-
Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке
 :
:
 ;
;

-
Исследовать на экстремум функцию
 ,
,

-
В какой точке
 эллипса
эллипса
 касательная к нему образует с осями
координат треугольник наименьшей
площади?
касательная к нему образует с осями
координат треугольник наименьшей
площади?
-
По заданным приближенным значениям аргументов функции
 и их предельным абсолютным погрешностям
вычислить абсолютную
и их предельным абсолютным погрешностям
вычислить абсолютную
 и относительную
и относительную
 (в процентах) погрешности значения
функции; найти приближенное значение
(в процентах) погрешности значения
функции; найти приближенное значение
 ,
сохраняя только верные цифры.
,
сохраняя только верные цифры.
 ;
;
 .
.
ТИПОВОЙ РАСЧЕТ
по теме “Функции нескольких переменных”
Вариант №14
-
Найти и изобразить в декартовой системе координат область определения функции:
а)
 ;
б)
;
б)
![]() ;
;
-
Для заданной функции найти все частные производные первого порядка:
а)
 ;
б)
;
б)
![]() ;
;
-
Для заданной функции найти требуемые частные и смешанные производные:
![]() ;
;

-
Проверить, что функция
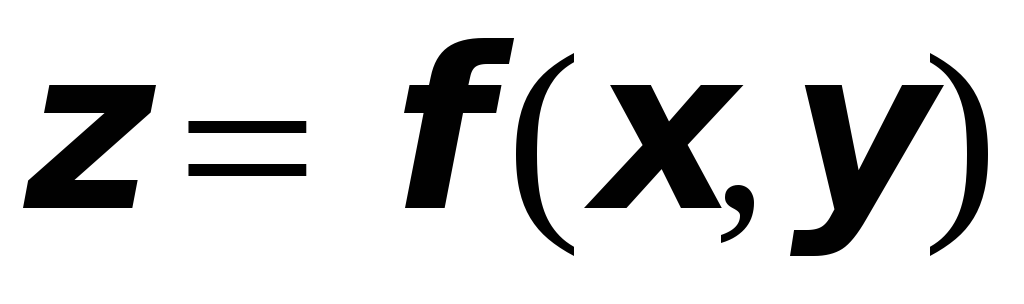 удовлетворяет заданному уравнению:
удовлетворяет заданному уравнению:
![]() ;
;

-
Найти производные неявно заданной функции: а)
 ;
б)
;
б)

1.
![]() ;
2.
;
2.
![]()
-
Найти градиент функции
 в точке
в точке
 и
вычислить его модуль
и
вычислить его модуль
![]() ;
;
![]()
-
Для функции
 в точке
в точке
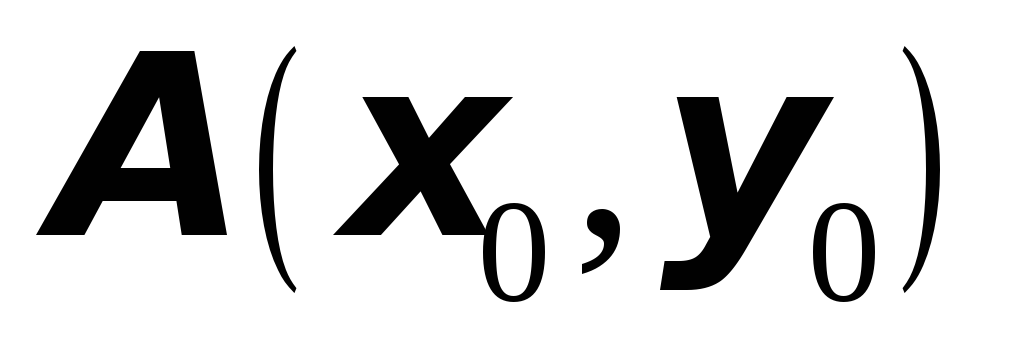 вычислить
градиент и производную в направлении
вектора
вычислить
градиент и производную в направлении
вектора

![]()
-
Найти полный дифференциал функции:
а)
![]() ;
б)
;
б)

-
С помощью полного дифференциала найти приближенное значение функции:
![]() при
при
![]()
-
Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке
 :
:
 ;
;

-
Исследовать на экстремум функцию
 ,
,

-
Из всех конусов с боковой поверхностью
 выделить
тот, у которого объем наибольший.
Определить радиус основания R
и высоту H этого
конуса.
выделить
тот, у которого объем наибольший.
Определить радиус основания R
и высоту H этого
конуса. -
По заданным приближенным значениям аргументов функции
 и их предельным абсолютным погрешностям
вычислить абсолютную
и их предельным абсолютным погрешностям
вычислить абсолютную
 и относительную
и относительную
 (в процентах) погрешности значения
функции; найти приближенное значение
(в процентах) погрешности значения
функции; найти приближенное значение
 ,
сохраняя только верные цифры.
,
сохраняя только верные цифры. ;
;
![]() .
.
ТИПОВОЙ РАСЧЕТ
по теме “Функции нескольких переменных”
Вариант №15
-
Найти и изобразить в декартовой системе координат область определения функции:
а)
![]() ;
б)
;
б)
![]() ;
;
-
Для заданной функции найти все частные производные первого порядка:
а)
![]() ;
б)
;
б)
![]() ;
;
-
Для заданной функции найти требуемые частные и смешанные производные:
![]() ;
;

-
Проверить, что функция
 удовлетворяет заданному уравнению:
удовлетворяет заданному уравнению:
 ;
;

-
Найти производные неявно заданной функции: а)
 ;
б)
;
б)

1.
![]() ;
2.
;
2.

-
Найти градиент функции
 в точке
в точке
 и
вычислить его модуль
и
вычислить его модуль
![]() ;
;
![]()
-
Для функции
 в точке
в точке
 вычислить
градиент и производную в направлении
вектора
вычислить
градиент и производную в направлении
вектора

![]()
-
Найти полный дифференциал функции:
а)
![]() ;
б)
;
б)
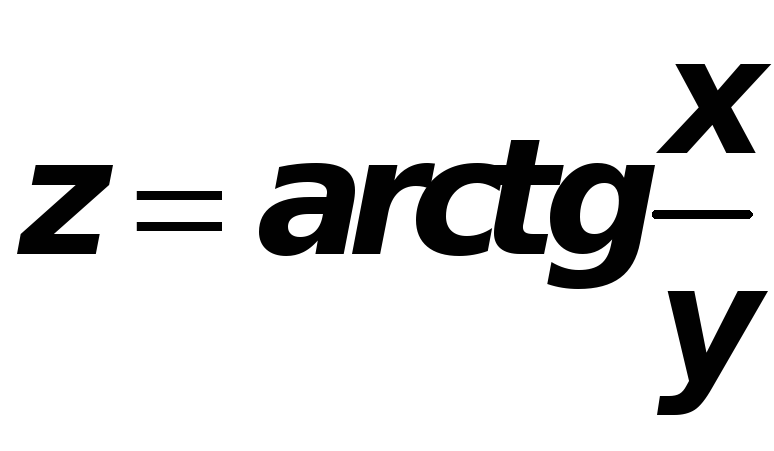
-
С помощью полного дифференциала найти приближенное значение функции:
![]() при
при
![]()
-
Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке
 :
:
 ;
;
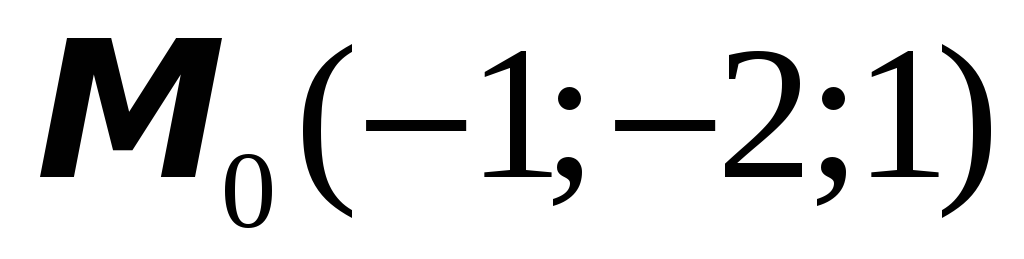
-
Исследовать на экстремум функцию
 ,
,

-
Найти наибольший объем V прямоугольного параллелепипеда при заданной сумме 12a всех его ребер.
-
По заданным приближенным значениям аргументов функции
 и их предельным абсолютным погрешностям
вычислить абсолютную
и их предельным абсолютным погрешностям
вычислить абсолютную
 и относительную
и относительную
 (в процентах) погрешности значения
функции; найти приближенное значение
(в процентах) погрешности значения
функции; найти приближенное значение
 ,
сохраняя только верные цифры.
,
сохраняя только верные цифры. ;
;
ТИПОВОЙ РАСЧЕТ
по теме “Функции нескольких переменных”
Вариант №16
-
Найти и изобразить в декартовой системе координат область определения функции:
а)
![]() ;
б)
;
б)
![]() ;
;
-
Для заданной функции найти все частные производные первого порядка:
а)
 ;
б)
;
б)
 ;
;
-
Для заданной функции найти требуемые частные и смешанные производные:
 ;
;

-
Проверить, что функция
 удовлетворяет заданному уравнению:
удовлетворяет заданному уравнению:
![]() ;
;

-
Найти производные неявно заданной функции: а)
 ;
б)
;
б)

1.
![]() ;
2.
;
2.
![]()
-
Найти градиент функции
 в точке
в точке
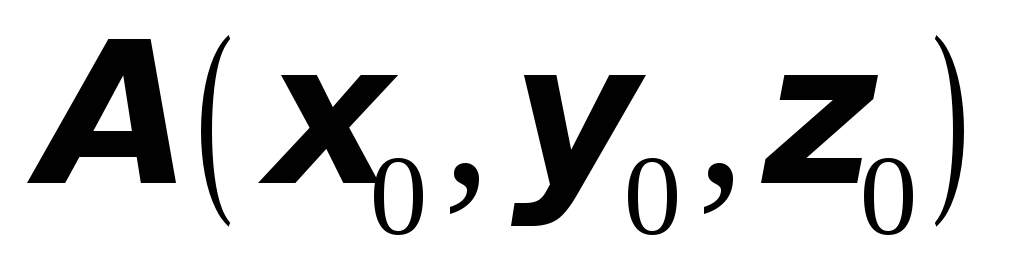 и
вычислить его модуль
и
вычислить его модуль
![]() ;
;
![]()
-
Для функции
 в точке
в точке
 вычислить
градиент и производную в направлении
вектора
вычислить
градиент и производную в направлении
вектора


-
Найти полный дифференциал функции:
а)
![]() ;
б)
;
б)

-
С помощью полного дифференциала найти приближенное значение функции:
![]() при
при
![]()
-
Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке
 :
:
 ;
;

-
Исследовать на экстремум функцию
 ,
,

-
Сечение канала должно иметь форму равнобочной трапеции с заданной площадью S. Как выбрать размеры сечения: L – боковую сторону трапеции, c – меньшее нижнее основание,
 - острый угол при большем верхнем
основании, - чтобы омываемая поверхность
канала была наименьшей?
- острый угол при большем верхнем
основании, - чтобы омываемая поверхность
канала была наименьшей?
13. По заданным приближенным значениям
аргументов функции
![]() и их предельным абсолютным погрешностям
вычислить абсолютную
и их предельным абсолютным погрешностям
вычислить абсолютную
![]() и относительную
и относительную
![]() (в процентах) погрешности значения
функции; найти приближенное значение
(в процентах) погрешности значения
функции; найти приближенное значение
![]() ,
сохраняя только верные цифры.
,
сохраняя только верные цифры.
 ;
;
![]()
![]() .
.
ТИПОВОЙ РАСЧЕТ
по теме “Функции нескольких переменных”
Вариант №17
-
Найти и изобразить в декартовой системе координат область определения функции:
а)
![]() ;
б)
;
б)
![]() ;
;
-
Для заданной функции найти все частные производные первого порядка:
а)
 ;
б)
;
б)
 ;
;
-
Для заданной функции найти требуемые частные и смешанные производные:
![]() ;
;
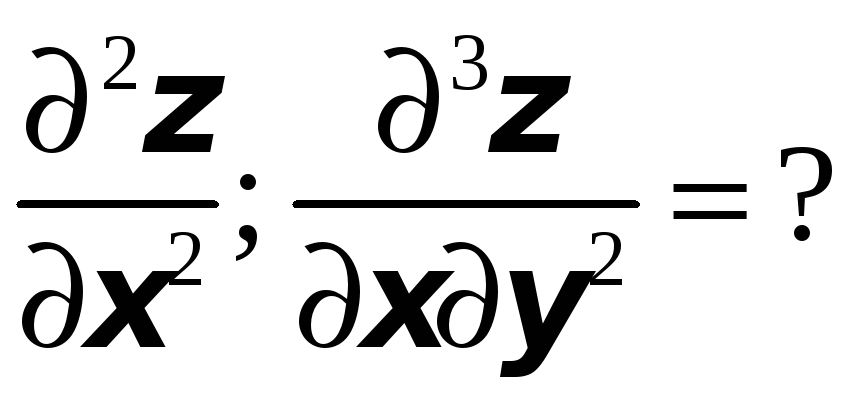
-
Проверить, что функция
 удовлетворяет заданному уравнению:
удовлетворяет заданному уравнению:
![]() ;
;

-
Найти производные неявно заданной функции: а)
 ;
б)
;
б)

1.
![]() ;
2.
;
2.
![]()
-
Найти градиент функции
 в точке
в точке
 и
вычислить его модуль
и
вычислить его модуль
![]() ;
;
![]()
-
Для функции
 в точке
в точке
 вычислить
градиент и производную в направлении
вектора
вычислить
градиент и производную в направлении
вектора


-
Найти полный дифференциал функции:
а)
![]() ;
б)
;
б)

-
С помощью полного дифференциала найти приближенное значение функции:
![]() при
при
![]()
-
Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке
 :
:
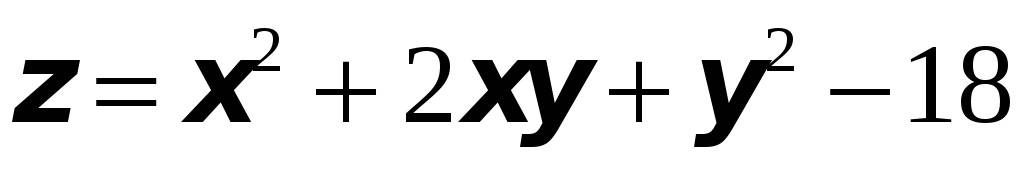 ;
;

-
Исследовать на экстремум функцию
 ,
,

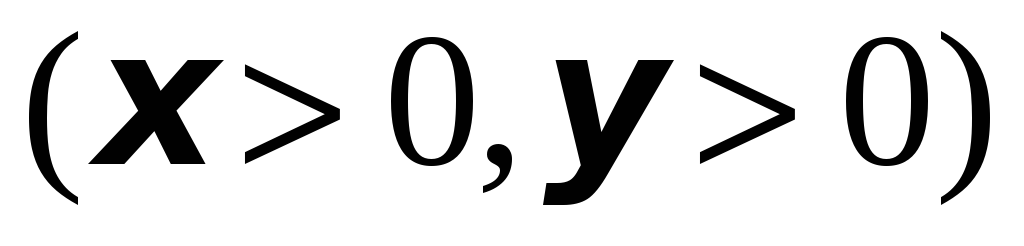
-
Найти размеры a, b, c прямоугольного параллелепипеда, имеющего при заданном объеме V наименьшую площадь полной поверхности.
13. По заданным приближенным значениям
аргументов функции
![]() и их предельным абсолютным погрешностям
вычислить абсолютную
и их предельным абсолютным погрешностям
вычислить абсолютную
![]() и относительную
и относительную
![]() (в процентах) погрешности значения
функции; найти приближенное значение
(в процентах) погрешности значения
функции; найти приближенное значение
![]() ,
сохраняя только верные цифры.
,
сохраняя только верные цифры.
 ;
;
![]() .
.
ТИПОВОЙ РАСЧЕТ
по теме “Функции нескольких переменных”
Вариант №18
-
Найти и изобразить в декартовой системе координат область определения функции:
а)
![]() ;
б)
;
б)
![]() ;
;
-
Для заданной функции найти все частные производные первого порядка:
а)
![]() ;
б)
;
б)
![]() ;
;
-
Для заданной функции найти требуемые частные и смешанные производные:
 ;
;

-
Проверить, что функция
 удовлетворяет заданному уравнению:
удовлетворяет заданному уравнению:
![]() ;
;

-
Найти производные неявно заданной функции: а)
 ;
б)
;
б)

1.
![]() ;
2.
;
2.
![]()
-
Найти градиент функции
 в точке
в точке
 и
вычислить его модуль
и
вычислить его модуль
![]() ;
;
![]()
-
Для функции
 в точке
в точке
 вычислить
градиент и производную в направлении
вектора
вычислить
градиент и производную в направлении
вектора

![]()
-
Найти полный дифференциал функции:
а)
![]() ;
б)
;
б)
![]()
-
С помощью полного дифференциала найти приближенное значение функции:
![]() при
при
![]()
-
Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке
 :
:
 ;
;

-
Исследовать на экстремум функцию
 ,
,

-
На эллипсе
 найти точку
найти точку
 ,
наименее удаленную от прямой 3x
+ y – 9 = 0.
,
наименее удаленную от прямой 3x
+ y – 9 = 0. -
По заданным приближенным значениям аргументов функции
 и их предельным абсолютным погрешностям
вычислить абсолютную
и их предельным абсолютным погрешностям
вычислить абсолютную
 и относительную
и относительную
 (в процентах) погрешности значения
функции; найти приближенное значение
(в процентах) погрешности значения
функции; найти приближенное значение
 ,
сохраняя только верные цифры.
,
сохраняя только верные цифры. ;
;
ТИПОВОЙ РАСЧЕТ
по теме “Функции нескольких переменных”
Вариант №19
-
Найти и изобразить в декартовой системе координат область определения функции:
а)
![]() ;
б)
;
б)
![]() ;
;
-
Для заданной функции найти все частные производные первого порядка:
а)
 ;
б)
;
б)
![]() ;
;
-
Для заданной функции найти требуемые частные и смешанные производные:
![]() ;
;
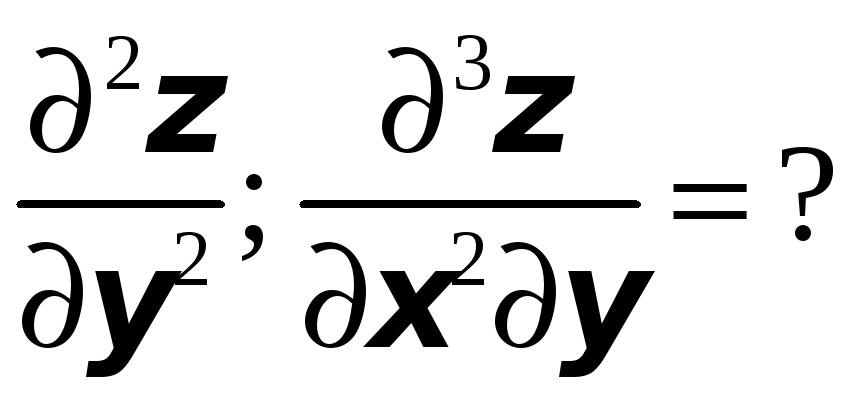
-
Проверить, что функция
 удовлетворяет заданному уравнению:
удовлетворяет заданному уравнению:
![]() ;
;
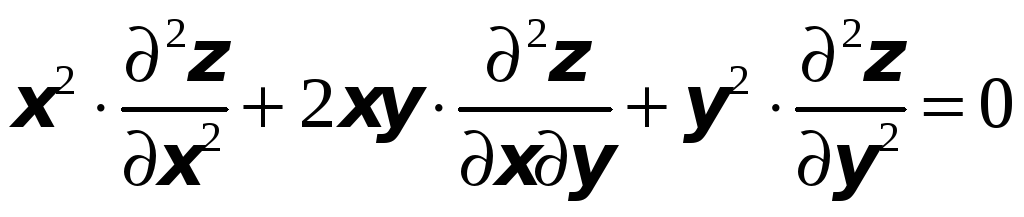
-
Найти производные неявно заданной функции: а)
 ;
б)
;
б)

1.
![]() ;
2.
;
2.
![]()
-
Найти градиент функции
 в точке
в точке
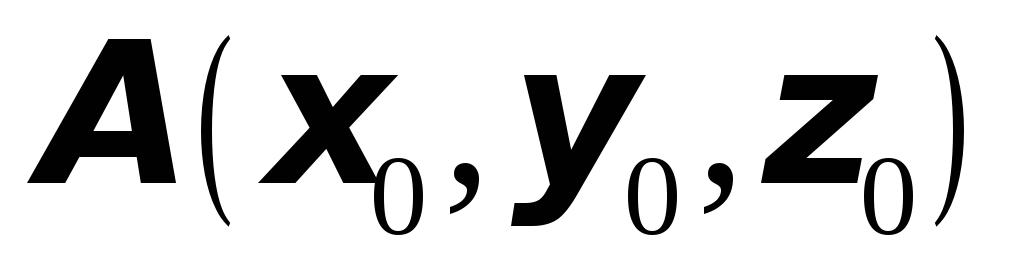 и
вычислить его модуль
и
вычислить его модуль
![]() ;
;
![]()
-
Для функции
 в точке
в точке
 вычислить
градиент и производную в направлении
вектора
вычислить
градиент и производную в направлении
вектора

![]()
-
Найти полный дифференциал функции:
а)
![]() ;
б)
;
б)
![]()
-
С помощью полного дифференциала найти приближенное значение функции:
![]() при
при
![]()
-
Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке
 :
:
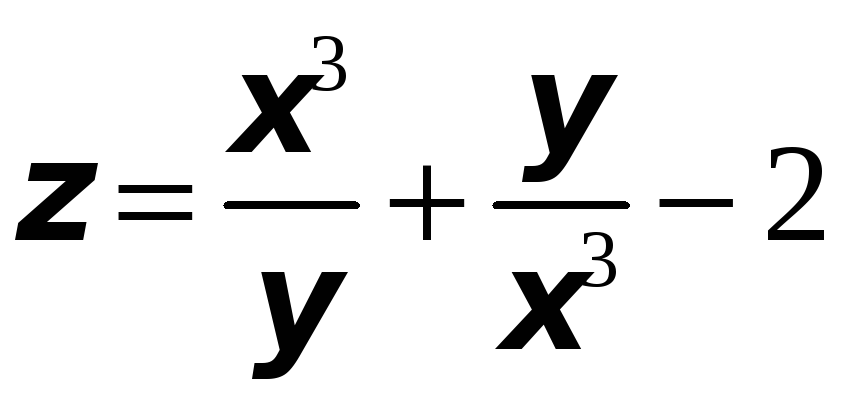 ;
;

-
Исследовать на экстремум функцию
 ,
,

-
Среди всех прямоугольных параллелепипедов, имеющих длину диагонали d , выделить тот, у которого объем наибольший. Определить размеры a, b, c такого параллелепипеда.
