
- •Алтайский государственный технический университет им. И.И. Ползунова
- •Оглавление
- •Дифференциальное исчисление
- •Свойства:
- •Самостоятельная работа Продифференцировать данные функции:
- •2. Специальные приемы дифференцирования
- •2.1. Логарифмическое дифференцирование
- •2.2. Дифференцирование функций, заданных неявно
- •2.3. Дифференцирование функций, заданных параметрически
- •Производные высших порядков
- •Дифференциал функции
- •Геометрический и физический смысл производной
- •Правило Лопиталя
- •Найти пределы следующих функций:
- •Самостоятельная работа
- •Примерный вариант контрольной работы
- •8. Возрастание и убывание функций
- •9. Максимум и минимум функции
- •10. Наибольшее и наименьшее значение функции
- •11. Решение задач на максимум и минимум
- •12. Направление выпуклости кривой. Точки перегиба
- •13. Асимптоты кривой
- •14. Исследование функции и построение графиков
- •15. Варианты типового расчета
9. Максимум и минимум функции
Точка
![]() называется точкоймаксимума
или минимума
функции
называется точкоймаксимума
или минимума
функции
![]() ,
если в некоторой окрестности точки
,
если в некоторой окрестности точки![]() выполняется неравенство
выполняется неравенство![]() или
или![]() соответственно. Значения функции в
точке
соответственно. Значения функции в
точке![]() называются соответственномаксимумом
(минимумом)
функции.
Максимум и минимум функции называется
экстремумом
функции.
Значения аргумента, при которых функция
имеет экстремум, называются критическими
точками первого рода.
называются соответственномаксимумом
(минимумом)
функции.
Максимум и минимум функции называется
экстремумом
функции.
Значения аргумента, при которых функция
имеет экстремум, называются критическими
точками первого рода.
Чтобы
найти экстремальные значения функции,
надо найти ее производную
![]() и, приравняв ее к нулю, решить уравнение
и, приравняв ее к нулю, решить уравнение![]() .
Корни этого уравнения, а также точки, в
которых производная не существует,
являются критическими точками первого
рода.
.
Корни этого уравнения, а также точки, в
которых производная не существует,
являются критическими точками первого
рода.
Если
знак производной при переходе через
точку
![]() меняется с плюса на минус, то
меняется с плюса на минус, то![]() есть точка максимума. Если знак производной
при переходе через точку
есть точка максимума. Если знак производной
при переходе через точку![]() меняется с минуса на плюс, то
меняется с минуса на плюс, то![]() есть точка минимума. Если знак не
меняется, то в точке
есть точка минимума. Если знак не
меняется, то в точке![]() экстремума нет.
экстремума нет.
Иногда
проще исследовать критическую точку
по знаку второй производной. Если в
критической точке, где первая производная
равна нулю,
![]() ,
то
,
то![]() есть точка минимума. Если
есть точка минимума. Если![]() ,
то
,
то![]() есть точка максимума. Если
есть точка максимума. Если![]() ,
то такую точку исследуют по первой
производной.
,
то такую точку исследуют по первой
производной.
Если
функция задана неявно
![]() ,
то для того, чтобы
,
то для того, чтобы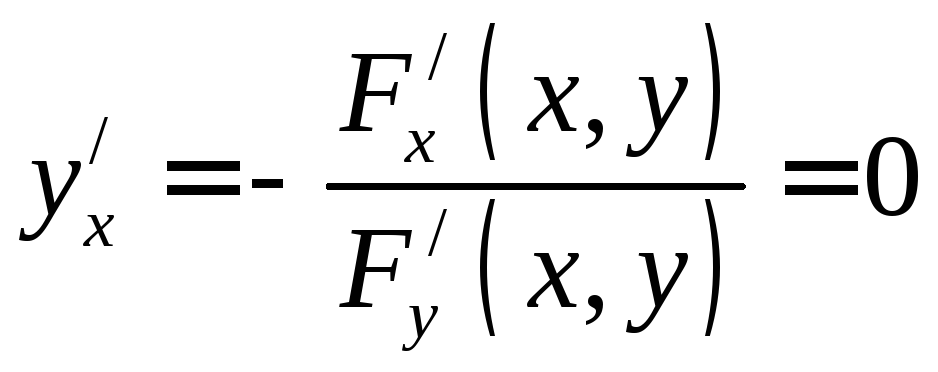 ,
должно выполняться равенство
,
должно выполняться равенство![]() .
Здесь
.
Здесь![]() ,
,![]() производные от функции
производные от функции![]() по
по![]() и
и![]() ,
найденные в предположении, что
,
найденные в предположении, что![]() и
и![]() не зависят от
не зависят от![]() и
и![]() ,
соответственно. Решая совместно
,
соответственно. Решая совместно![]() и
и![]() ,
находим критические точки. Экстремум
функции в критических точках находят
по знаку второй производной
,
находим критические точки. Экстремум
функции в критических точках находят
по знаку второй производной![]() .
Если в критической точке
.
Если в критической точке![]() ,
то это точка максимума. Если
,
то это точка максимума. Если![]() ,
то это точка минимума.
,
то это точка минимума.
Пример
1. Исследовать
на экстремум функцию
![]() .
.
Решение:
Находим производную
![]() и приравняем ее к нулю
и приравняем ее к нулю![]() .
Корни этого уравнения
.
Корни этого уравнения![]() ,
,![]() являются критическими точками.
являются критическими точками.
При
переходе через точку
![]() производная знака не меняет, т.к. данный
множитель в квадрате, а при переходе
через точку
производная знака не меняет, т.к. данный
множитель в квадрате, а при переходе
через точку![]() меняет знак с минуса на плюс. Значит, в
точке
меняет знак с минуса на плюс. Значит, в
точке![]() функция имеет минимум. Находим
экстремальные значения функции, а именно
минимум функции
функция имеет минимум. Находим
экстремальные значения функции, а именно
минимум функции![]() .
.
Пример
2. Исследовать
на экстремум функцию
![]() .
.
Решение:
Находим первую производную
![]() и приравняем ее к нулю
и приравняем ее к нулю![]() .
Корни этого уравнения
.
Корни этого уравнения![]() ,
,![]() ,
,![]() являются критическими точками. Находим
вторую производную
являются критическими точками. Находим
вторую производную![]() и выясним знак второй производной в
критических точках:
и выясним знак второй производной в
критических точках:![]() - функция имеет максимум;
- функция имеет максимум;![]() - функция имеет минимум;
- функция имеет минимум;![]() функция имеет минимум. Определяем
экстремальные значения функции:
функция имеет минимум. Определяем
экстремальные значения функции:![]() - максимум функции;
- максимум функции;![]() - минимум функции;
- минимум функции;![]() - минимум функции.
- минимум функции.
Пример
3. Исследовать
на экстремум функцию
![]() .
.
Решение:
Находим первую производную
![]() и приравниваем ее к нулю
и приравниваем ее к нулю![]() .
Корни этого уравнения
.
Корни этого уравнения![]() ,
,![]() Являются критическими точками. Находим
вторую производную
Являются критическими точками. Находим
вторую производную![]() и выясним знак в критических точках.
и выясним знак в критических точках.
В
точке
![]() вторая производная
вторая производная![]() - функция имеет максимум. В точке
- функция имеет максимум. В точке![]() вторая производная
вторая производная![]() ,
следовательно, судить об экстремуме
нельзя. Проверим наличие экстремума по
первой производной. Поскольку при
переходе через точку
,
следовательно, судить об экстремуме
нельзя. Проверим наличие экстремума по
первой производной. Поскольку при
переходе через точку![]() первая производная знака не меняет, то
в точке
первая производная знака не меняет, то
в точке![]() экстремума нет.
экстремума нет.
Определяем
в точке
![]() максимальное значение функции
максимальное значение функции![]() .
.
Пример
4. Исследовать
на экстремум функцию
![]() .
.
Решение:
Функция определена на всей числовой
оси. Находим производную
![]() .
Приравниваем производную к нулю
.
Приравниваем производную к нулю![]() и находим критическую точку
и находим критическую точку![]() .
При переходе через точку
.
При переходе через точку![]() производная
производная![]() меняет знак с минуса на плюс, следовательно,
в точке
меняет знак с минуса на плюс, следовательно,
в точке![]() функция имеет минимум
функция имеет минимум![]() .
.
Приравнивая
к нулю знаменатель производной, получаем
![]() .
Отсюда находим критическую точку функции
.
Отсюда находим критическую точку функции![]() ,
в которой производная не существует.
Очевидно, что в точке
,
в которой производная не существует.
Очевидно, что в точке![]() производная
производная![]() ,
а в точке
,
а в точке![]() производная
производная![]() .
Следовательно,
.
Следовательно,![]() есть точка максимума функции
есть точка максимума функции![]() .
.
Пример
5. Исследовать
на экстремум функцию
![]() .
.
Решение:
Функция задана неявно. Находим
![]() и
и![]() .
Производная
.
Производная![]() тогда, когда
тогда, когда![]() ,
т.е.
,
т.е.![]() .
.
Решая
систему уравнений
 находим критическую
находим критическую![]() .
Вычисляем вторую производную
.
Вычисляем вторую производную![]() .
В критической точке
.
В критической точке![]() и
и![]() ,
если
,
если![]() ,
и
,
и![]() ,
если
,
если![]() .
Таким образом, функция
.
Таким образом, функция![]() при
при![]() имеет минимум, а при
имеет минимум, а при![]() имеет максимум.
имеет максимум.
Найти максимум и минимум функции:
1.
![]() .
Ответ:
.
Ответ:![]() .
.
2.
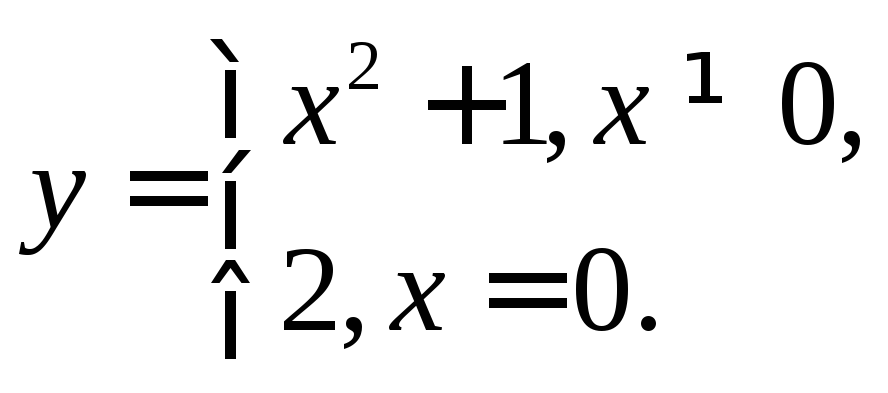 Ответ:
Ответ:![]() .
.
3.
![]() .
Ответ:
.
Ответ:![]() .
.
4.
![]() .
Ответ:
.
Ответ:![]() ,
,![]() .
.
5.
 .
Ответ:
.
Ответ:![]() ,
,![]() ,
,![]() .
.
6.
![]() .
Ответ:
.
Ответ:![]() ,
,
![]() .
.
7.
![]() .
Ответ:
экстремумов нет.
.
Ответ:
экстремумов нет.
8.
![]() .
Ответ:
.
Ответ:![]() ,
,![]() .
.
9.
![]() .
Ответ:
.
Ответ:![]() ,
,![]() .
.
10.
![]() .
Ответ:
.
Ответ:![]() .
.
11.
![]() .
Ответ:
.
Ответ:![]() ,
,![]() .
.
12.
![]() .
Ответ:
.
Ответ:![]() ,
,![]() .
.
13.
![]() .
Ответ:
.
Ответ:![]() .
.
14.
![]() .
Ответ:
.
Ответ:![]() .
.
15.
![]() .
Ответ:
.
Ответ:![]() .
.
16.
![]() .
Ответ:
.
Ответ:![]() ,
,![]() .
.
17.
![]() .
Ответ:
.
Ответ:![]() ,
,![]() .
.
18.
![]() Ответ:
Ответ:![]() ,
,![]() .
.
19.
 Ответ:
Ответ:![]() ,
,![]() .
.
20.
.
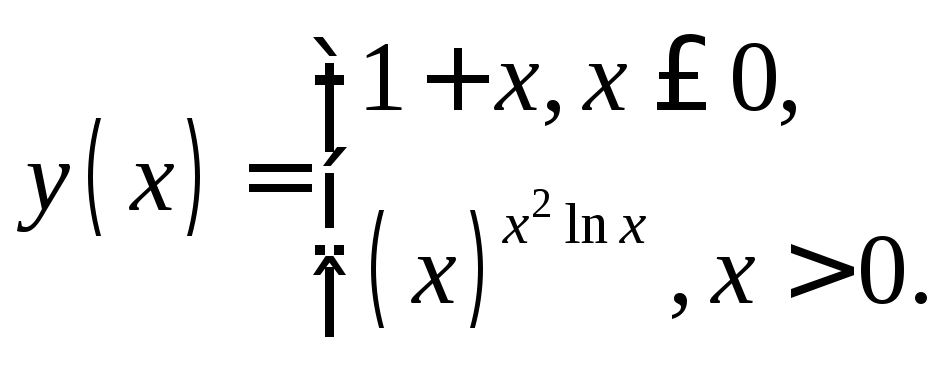 Ответ:
Ответ:![]() ,
,![]() .
.
21.
неявная функция:
![]() .
.
Ответ:
![]() ,
,![]() .
.
22.
неявная функция:
![]() .
.
Ответ:
![]() ,
,![]() .
.
23.
параметрически заданная функция:

![]() .
.
Ответ:
![]() .
.
24.
параметрически заданная функция:

Ответ:
![]() .
.
25.
![]() .
Ответ:
.
Ответ:![]() ,
,
если
![]() четное, то
четное, то![]() .
.
26.
 .
.
Ответ:
![]() ,
если
,
если![]() нечетное;
нечетное;
если
![]() четное, то экстремумов нет.
четное, то экстремумов нет.
27.
![]() .
Ответ:
.
Ответ: ,
,
если
![]() четное, то
четное, то![]() ,
если
,
если![]() четное, то
четное, то![]() .
.
