
- •Алтайский государственный технический университет им. И.И. Ползунова
- •Оглавление
- •Дифференциальное исчисление
- •Свойства:
- •Самостоятельная работа Продифференцировать данные функции:
- •2. Специальные приемы дифференцирования
- •2.1. Логарифмическое дифференцирование
- •2.2. Дифференцирование функций, заданных неявно
- •2.3. Дифференцирование функций, заданных параметрически
- •Производные высших порядков
- •Дифференциал функции
- •Геометрический и физический смысл производной
- •Правило Лопиталя
- •Найти пределы следующих функций:
- •Самостоятельная работа
- •Примерный вариант контрольной работы
- •8. Возрастание и убывание функций
- •9. Максимум и минимум функции
- •10. Наибольшее и наименьшее значение функции
- •11. Решение задач на максимум и минимум
- •12. Направление выпуклости кривой. Точки перегиба
- •13. Асимптоты кривой
- •14. Исследование функции и построение графиков
- •15. Варианты типового расчета
Геометрический и физический смысл производной
Геометрически
производная
![]() функции
функции![]() представляет угловой коэффициент
представляет угловой коэффициент![]() касательной к графику этой функции в
точке
касательной к графику этой функции в
точке![]() .
.
Если
на плоскости задана точка
![]() и кривая как график явной функции
и кривая как график явной функции![]() то:
то:
![]() -
уравнение касательной в точке с абсциссой
-
уравнение касательной в точке с абсциссой
![]() ,
,
![]() ,
,
![]() - уравнение нормали в точке с абсциссой
- уравнение нормали в точке с абсциссой![]() .
Если
.
Если![]() ,
то уравнения касательной и нормали
имеют вид соответственно:
,
то уравнения касательной и нормали
имеют вид соответственно:![]() ,
,![]() .
.
При
параметрическом задании кривой
 уравнения касательной и нормали
записываются соответственно:
уравнения касательной и нормали
записываются соответственно:
 ,
,
![]() ,
,
 ,
,
![]() .
.
Угол
между кривыми
![]() и
и![]() в точке их пересечения
в точке их пересечения
![]() –
это угол между касательными к этим
кривым в точке
–
это угол между касательными к этим
кривым в точке![]() .
Этот угол находится по формуле:
.
Этот угол находится по формуле: .
.
Если
в точке
![]() производная не определена, но функция
имеет различные односторонние пределы
производная не определена, но функция
имеет различные односторонние пределы![]() и
и![]() ,
то в этой точке графика функции существуют
две различные с соответствующими
угловыми коэффициентами
,
то в этой точке графика функции существуют
две различные с соответствующими
угловыми коэффициентами![]() ,
,![]() односторонние касательные, составляющие
угол, а точка называетсяугловой.
односторонние касательные, составляющие
угол, а точка называетсяугловой.
Если
![]() ,
т.е. функция имеет бесконечную производную,
то она не дифференцируема в этой точке.
В этом случае график функции имеет
вертикальную касательную (точка
перегиба).
,
т.е. функция имеет бесконечную производную,
то она не дифференцируема в этой точке.
В этом случае график функции имеет
вертикальную касательную (точка
перегиба).
Если
в точке
![]() функция имеет бесконечные односторонние
производные разных знаков, то график
функции имеет две слившиеся вертикальные
касательные (асимптоты).
функция имеет бесконечные односторонние
производные разных знаков, то график
функции имеет две слившиеся вертикальные
касательные (асимптоты).
Если
при прямолинейном движении точки задан
закон движения
![]() ,
то скорость движения в момент
,
то скорость движения в момент![]() есть производная пути по времени:
есть производная пути по времени:![]() ,
ускорение в момент
,
ускорение в момент![]() есть
есть![]() .
.
При
движении точки по окружности: угловая
скорость вращения
![]() в данный момент равна производной от
угла поворота
в данный момент равна производной от
угла поворота![]() по времени:
по времени:![]() .
Угловое ускорение точки есть первая
производная от угловой скорости
.
Угловое ускорение точки есть первая
производная от угловой скорости![]() или вторая производная от угла поворота
по времени
или вторая производная от угла поворота
по времени![]() .
.
Сила
тока в данный момент времени равна
производной от количества протекшего
электричества по времени:
![]() .
.
Химическое
истолкование производной. Пусть
![]() - концентрация вещества, получаемого в
ходе химической реакции в момент времени
- концентрация вещества, получаемого в
ходе химической реакции в момент времени![]() .
Тогда
.
Тогда![]() - скорость реакции в момент
- скорость реакции в момент![]() .
.
Пример
1. В
точках пересечения эллипсов
![]() ,
,![]() найти угол между ними.
найти угол между ними.
Решение: Эллипсы расположены симметрично относительно координатных осей. Поэтому рассмотрим только первый квадрат координатной плоскости.
Решив
систему
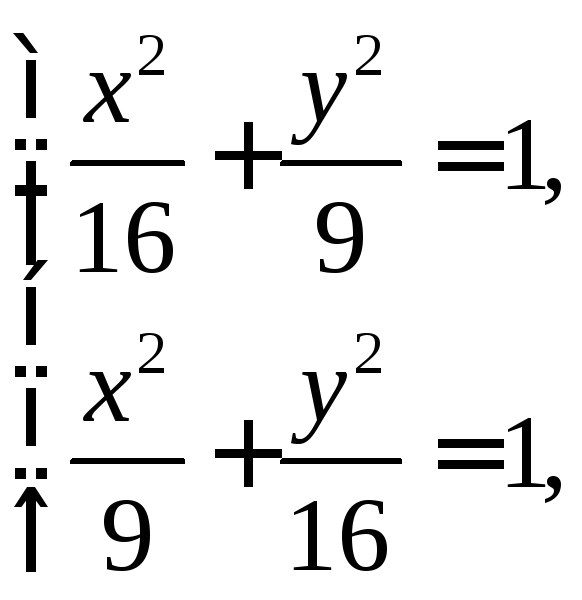 найдем точку пересечения эллипсов
найдем точку пересечения эллипсов![]() .
Из уравнения первого эллипса получаем
.
Из уравнения первого эллипса получаем![]() ,
т.е.
,
т.е.![]() .
Следовательно
.
Следовательно![]() .
Аналогично, для второго эллипса получим
.
Аналогично, для второго эллипса получим![]() .
По формуле
.
По формуле ,
,![]() получим:
получим: .
.
Итак,
эллипсы пересекаются в четырех точках
под углом
![]() ,
т.е. под углом, равным приблизительно
,
т.е. под углом, равным приблизительно![]() .
.
Пример
2. Высота
![]() снаряда, вылетевшего с начальной
скоростью
снаряда, вылетевшего с начальной
скоростью![]() под углом
под углом![]() к горизонту, изменяется по закону
к горизонту, изменяется по закону![]() ,
где
,
где![]() - время,
- время,![]() - ускорение силы тяжести. В какой момент
скорость изменения высоты снаряда над
горизонтом равна нулю?
- ускорение силы тяжести. В какой момент
скорость изменения высоты снаряда над
горизонтом равна нулю?
Решение:
Вычислим производную функции
![]() .
.
Следовательно,
скорость изменения высоты снаряда нал
горизонтом равна нулю при
![]() .
.
Найти уравнения касательной и нормали к данной кривой в данной точке:
1.
![]() ,
,![]() .
.
2.
 ,
,![]() .
Ответ:
.
Ответ:![]() ,
,![]() .
.
3.
 ,
,![]() .
.
4.

![]() .
.
5.
к эллипсу
![]() ,
,![]() .
.
6.
![]() ,
,![]() .
Ответ:
.
Ответ:![]() .
.
7.
![]() ;
;
![]() .
Ответ:
.
Ответ:
![]() .
.
8.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
9.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
10.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
11.
 ,
,
![]() .
Ответ:
.
Ответ:![]() .
.
12.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
13.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
14.
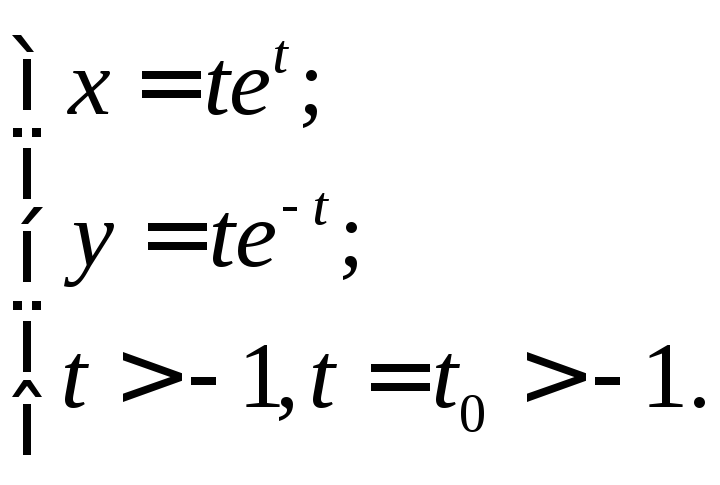 Ответ:
Ответ:
![]() .
.
15.

![]() .
Ответ:
.
Ответ:
![]() .
.
16.
Найти углы, под которыми пересекаются
линии, заданные уравнениями
![]() и
и![]() .
Ответ:
.
Ответ:![]() ,
,![]() .
.
17. Найти угол между кривыми:
a)
![]() и
и![]() .
Ответ:
.
Ответ:![]() .
.
b)
![]() и
и![]() .
Ответ:
.
Ответ:![]() .
.
Найти
углы, под которыми график функции
![]() пересекает ось абсцисс:
пересекает ось абсцисс:
18.
![]() .
Ответ:
.
Ответ:![]() .
.
19.
![]() .
Ответ: В точках
.
Ответ: В точках![]() синусоида
синусоида
пересекает
ось абсцисс под углом
![]() .
.
20.
![]() .
Ответ: В точках
.
Ответ: В точках![]() угол
угол![]() ,
,
в
точках
![]() угол
угол![]() .
.
21.
![]() .
Ответ:
.
Ответ:![]() .
.
22.
![]() .
.
Ответ:
в точке
![]() угол
угол![]() ,
в точке
,
в точке![]() угол
угол![]() .
.
23.
![]() .
Ответ:
.
Ответ:![]() .
.
24.
![]() .
Ответ:
.
Ответ:![]() .
.
25.
![]() .
.
Ответ:
в точках
![]() и
и![]() угол
угол![]() ,
,
в
точке
![]() угол
угол![]() .
.
26.
![]() .
.
Ответ:
в точке
![]() угол
угол![]() ,
,
в
точке
![]() угол
угол![]() .
.
27.
 Ответ:
Ответ:![]() .
.
28.
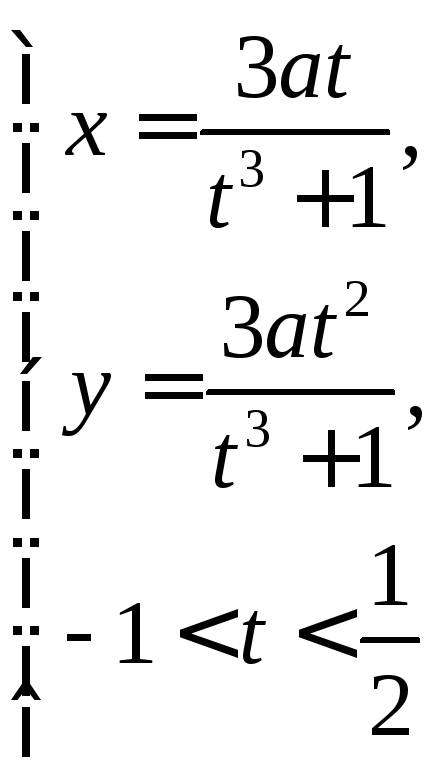 Ответ: 0.
Ответ: 0.
29.
![]() .
.
Ответ:
в точке
![]() угол
угол![]() ,
,
в
точке
![]() угол
угол![]() .
.
Найти
точки, в которых касательные к графику
функции
![]() параллельны оси абсцисс:
параллельны оси абсцисс:
30.
![]() .
Ответ: (-1;14), (2;-13).
.
Ответ: (-1;14), (2;-13).
31.
![]() .
Ответ: (0;-1), (1;-6), (-2;-33).
.
Ответ: (0;-1), (1;-6), (-2;-33).
32.
![]() .
Ответ: (-1;-58), (1;54), (7;-2106).
.
Ответ: (-1;-58), (1;54), (7;-2106).
33.
![]() .
Ответ:
.
Ответ:
![]() .
.
34.
![]() .
Ответ:
.
Ответ:
![]() .
.
35.
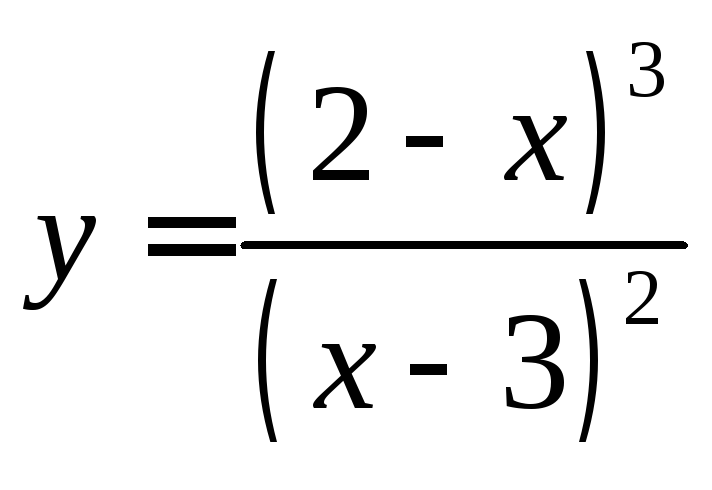 .
Ответ:
.
Ответ:
![]() .
.
36.
![]() .
Ответ:
.
Ответ:
![]() .
.
37.
 Ответ:
Ответ:
![]() .
.
38.
![]() .
Ответ:
.
Ответ:
![]() .
.
39.
На кривой
![]() найти точку
найти точку![]() ,
в которой касательная параллельна
прямой
,
в которой касательная параллельна
прямой![]() .
Ответ:
.
Ответ:![]() .
.
40.
Найти точку линии
![]() ,
в которой касательная перпендикулярна
прямой
,
в которой касательная перпендикулярна
прямой![]() ,
составить уравнение этой касательной.
Сделать чертеж.
Ответ:
,
составить уравнение этой касательной.
Сделать чертеж.
Ответ:![]() .
.
41.
Точка движется вдоль прямой по закону
![]() .
Найти скорость и ускорение точки в
момент времени
.
Найти скорость и ускорение точки в
момент времени![]() .
.
Ответ:
![]() .
.
42.
Угол поворота шкива в зависимости от
времени задан формулой
![]() .
Найти угловую скорость и ускорение при
.
Найти угловую скорость и ускорение при![]() .
.
Ответ:
угловая скорость равна
![]() ,
,
а
угловое ускорение не зависит от времени
и равно
![]() .
.
Определить, в каких точках и под каким углом пересекаются кривые:
43.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
44.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
45.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
46.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
47.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
48.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
49.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
50.
![]() ,
,
![]() .
Ответ:
.
Ответ:
![]() .
.
51.
 и
и
![]() .
Ответ:
.
Ответ:
![]() .
.
52.
 и
и
![]() .
Ответ:
.
Ответ:
![]() .
.
53.
Найти уравнение нормали к эллипсу
![]() в точке
в точке![]() .Ответ:
.Ответ:
![]() .
.
54.
Найти уравнение нормали к гиперболе
![]() в точке
в точке![]() .
.
Ответ:![]() .
.
Найти угол между касательной и полярным радиусом точки касания для следующих кривых:
55.
Спирали Архимеда
![]() .
Ответ:
.
Ответ:![]() .
.
56.
Гиперболической спирали
![]() .
Ответ:
.
Ответ:![]() .
.
57.
Логарифмической спирали
![]() .
Ответ:
.
Ответ:![]() .
.
58.
Кардиоиды
![]() .
Ответ:
.
Ответ:![]() .
.
59.
Дуги лемнискаты Бернулли
![]() .
Ответ:
.
Ответ:![]() .
.
60.
Точка движется по параболе
![]() так, что ее абсцисса изменяется по закону
так, что ее абсцисса изменяется по закону![]() (
(![]() измеряется в метрах,
измеряется в метрах,![]() - в секундах). Какова скорость изменения
ординаты точки через 9 с после начала
движения?
Ответ:
- в секундах). Какова скорость изменения
ординаты точки через 9 с после начала
движения?
Ответ:![]() .
.
61.
Радиус шара возрастает равномерно со
скоростью 5![]() .
Какова скорость изменения объема шара
в момент, когда его радиус становится
равным 50
.
Какова скорость изменения объема шара
в момент, когда его радиус становится
равным 50![]() ?
Ответ: 0,05
?
Ответ: 0,05![]() .
.
62.
Колесо вращается так, что угол поворота
пропорционален квадрату времени. Первый
оборот сделан за 8 с. Найти угловую
скорость через 64 с после начала движения.
Ответ:
![]() .
.
63.
По оси абсцисс движутся две точки,
имеющие законы движения:
![]() и
и![]() .
С какой скоростью удаляются они друг
от друга в момент встречи (
.
С какой скоростью удаляются они друг
от друга в момент встречи (![]() измеряется в метрах,
измеряется в метрах,![]() - в секундах)? Ответ:
- в секундах)? Ответ:![]() .
.
64.
Паром подтягивается к берегу при помощи
каната, который наматывается на ворот
со скоростью 3![]() .
Определить скорость движения парома в
тот момент, когда он находится в 25 м от
берега, если ворот расположен на берегу
выше поверхности воды на 4м.
.
Определить скорость движения парома в
тот момент, когда он находится в 25 м от
берега, если ворот расположен на берегу
выше поверхности воды на 4м.
Ответ:
![]() .
.
65.
Под каким углом пересекаются кривые
![]() и
и![]() в точке (1;1)?
Ответ:
в точке (1;1)?
Ответ:![]() .
.
66.
Определить среднюю скорость изменения
функции
![]() на отрезке
на отрезке![]() .
Ответ:
.
Ответ:![]() .
.
67.
Найти расстояние от полюса до произвольной
касательной кривой
![]() .
Ответ:
.
Ответ:![]() .
.
68.
Записать в декартовых и в полярных
координатах уравнение нормали к кардиоиде
![]() в точке с полярным углом
в точке с полярным углом![]() .
.
Ответ:
![]() ,
, .
.
69.
Точка движется по спирали Архимеда
![]() так, что угловая скорость вращения ее
полярного радиуса постоянна и равна
так, что угловая скорость вращения ее
полярного радиуса постоянна и равна![]() в секунду. Определить скорость удлинения
полярного радиуса
в секунду. Определить скорость удлинения
полярного радиуса![]() ,
если
,
если![]() .
Ответ:
.
Ответ:![]() .
.
