
- •Алтайский государственный технический университет им. И.И. Ползунова
- •Оглавление
- •Дифференциальное исчисление
- •Свойства:
- •Самостоятельная работа Продифференцировать данные функции:
- •2. Специальные приемы дифференцирования
- •2.1. Логарифмическое дифференцирование
- •2.2. Дифференцирование функций, заданных неявно
- •2.3. Дифференцирование функций, заданных параметрически
- •Производные высших порядков
- •Дифференциал функции
- •Геометрический и физический смысл производной
- •Правило Лопиталя
- •Найти пределы следующих функций:
- •Самостоятельная работа
- •Примерный вариант контрольной работы
- •8. Возрастание и убывание функций
- •9. Максимум и минимум функции
- •10. Наибольшее и наименьшее значение функции
- •11. Решение задач на максимум и минимум
- •12. Направление выпуклости кривой. Точки перегиба
- •13. Асимптоты кривой
- •14. Исследование функции и построение графиков
- •15. Варианты типового расчета
2.2. Дифференцирование функций, заданных неявно
Пусть
функция
![]() задана уравнением
задана уравнением![]() ,
не разрешенным относительно
,
не разрешенным относительно![]() ,
то есть функция
,
то есть функция![]() есть неявная функция от
есть неявная функция от![]() .
.
Чтобы
найти производную от неявной функции
![]() аргумента
аргумента![]() ,
дифференцируем по
,
дифференцируем по![]() обе части этого равенства, считая
обе части этого равенства, считая![]() функцией
функцией![]() .
В результате получим уравнение, линейное
относительно искомой производной. Решая
его, получим
.
В результате получим уравнение, линейное
относительно искомой производной. Решая
его, получим![]() ,
которая, как правило, будет зависеть от
,
которая, как правило, будет зависеть от![]() и
и![]() ,
т.е.
,
т.е.![]() .
.
Найти
производную
![]() :
:
1.
![]() .
2.
.
2.![]() .
.
3.
![]() .
4.
.
4.![]() .
.
5.
![]() .
6.
.
6.![]() .
.
7.
![]() .
8.
.
8.![]() .
.
9.
![]() .
.
10.
![]() .
.
2.3. Дифференцирование функций, заданных параметрически
Если
функциональная зависимость между
переменными
![]() и
и![]() задана параметрически:
задана параметрически: то производная от
то производная от![]() по
по![]() равна:
равна:![]() ,
а от
,
а от![]() по
по![]() :
:![]() .
.
Найти
производную
![]() :
:
1.
 2.
2.
3.
 4.
4.
5.
 6.
6.
7.
 8.
8.
9.
 10.
10.
Производные высших порядков
Производной n-го порядка называется производная от производной (n-1)-го порядка.
Пример
1. Найти
производные до n-го
порядка включительно от функции
![]() .
.
Решение:
![]() ,
,![]() ,
,![]() ,
,![]() и т. д.
и т. д.
Очевидно,
что производная n-го
порядка
![]() .
.
Вторая
производная от неявной функции
![]() находится дифференцированием функции
находится дифференцированием функции![]() по переменной
по переменной![]() ,
учитывая при этом, что
,
учитывая при этом, что![]() есть функция от
есть функция от![]() .
.
Пример
2. Найти
![]() для неявной функции
для неявной функции![]() .
.
Решение:
Дифференцируем
правую и левую часть по
![]() :
:![]() .
.
Разрешая
относительно производной, получим:
![]() .
.
Дифференцируем
еще один раз по
![]() :
: .
.
Подставляя
в последнее выражение значение
![]() ,
получим
,
получим

 .
.
Вторая
производная от функции
![]() по
по![]() ,
заданной параметрически,
равна
,
заданной параметрически,
равна

 .
.
Третья
производная
 и т.д.
и т.д.
Пример
3. Найти
![]() для функции
для функции .
.
Решение:
Найдем первую производную:
![]() .
.
Вторую производную находим по формуле:
 .
.
Производная n-го порядка от произведения двух функций удобнее находить по формуле Лейбница.
![]()
![]() ,
где
,
где
![]() - биномиальные коэффициенты,
- биномиальные коэффициенты,![]() ,
,![]() .
.
Пример
4. Найти
![]() для функции
для функции![]() .
.
Решение:
Положим
![]() ,
,![]() .
Тогда
.
Тогда![]() ,
,![]() ,
,![]() ,
,![]() .
По формуле Лейбница все слагаемые, кроме
трех последних, равны нулю, поэтому
получаем:
.
По формуле Лейбница все слагаемые, кроме
трех последних, равны нулю, поэтому
получаем:
![]()
![]() .
.
Для данных функций найти производные указанного порядка:
1.
![]() ,
,![]() -?
-?
2.
![]() ,
,![]() - ?
- ?
3.
![]() ,
,![]() -?
-?
4.
![]() ,
,![]() -?
-?
5.
![]() ,
,![]() -?
-?
6.
![]() ,
,![]() -?
-?
7.
![]() ,
,![]() -?
-?
8.
![]() ,
,![]() - ? Ответ:
- ? Ответ:![]() ,
,![]()
9.
![]() ,
,![]() - ? Ответ:
- ? Ответ:![]() .
.
Если
![]() ,
то
,
то .
Если
.
Если![]() ,
то
,
то .
.
10.
![]() ,
,![]() -? Ответ:
-? Ответ:![]() .
.
11.
![]() ,
,![]() - ? Ответ:
- ? Ответ:![]() .
.
12.
![]() ,
,![]() -? Ответ:
-? Ответ:![]() .
.
13.
![]() ,
,![]() -? Ответ:
-? Ответ:![]() .
.
14.
![]() ,
,![]() -? Ответ:
-? Ответ: .
.
15.
![]() ?
?
![]() -? Ответ:
-? Ответ:
![]() .
.
16.
![]() ,
,![]() -? Ответ:
-? Ответ:![]() .
.
17.
![]() ,
,![]() -? Ответ:
-? Ответ:![]() .
.
18.

![]() -? Ответ:
-? Ответ:![]() .
.
19.

![]() -? Ответ:
-? Ответ:![]() .
.
20.
![]()
![]() - ? Ответ:
- ? Ответ:![]() .
.
21.

![]() - ? Ответ:
- ? Ответ: .
.
22.

![]() - ? Ответ:
- ? Ответ: .
.
23.
![]()
![]() -? Ответ:
-? Ответ: .
.
24.
![]()
![]() -? Ответ:
-? Ответ: .
.
25.
![]() ,
,![]() -? Ответ:
-? Ответ: .
.
26.
![]() ,
,![]() -?
-?
Ответ:
 .
.
27.
![]() ,
,![]() - ? Ответ:
- ? Ответ:

28.
![]() ,
,![]() - ? Ответ:
- ? Ответ:![]() .
.
29.
![]() ,
,![]() - ?
- ?
Ответ:
![]() .
.
30.
![]() ,
,![]() -?
-?
Ответ:
![]()
![]() .
.
31.
![]() ,
,![]() -?
Ответ:
-?
Ответ: .
.
32.
![]() ,
,![]() - ? Ответ:
- ? Ответ: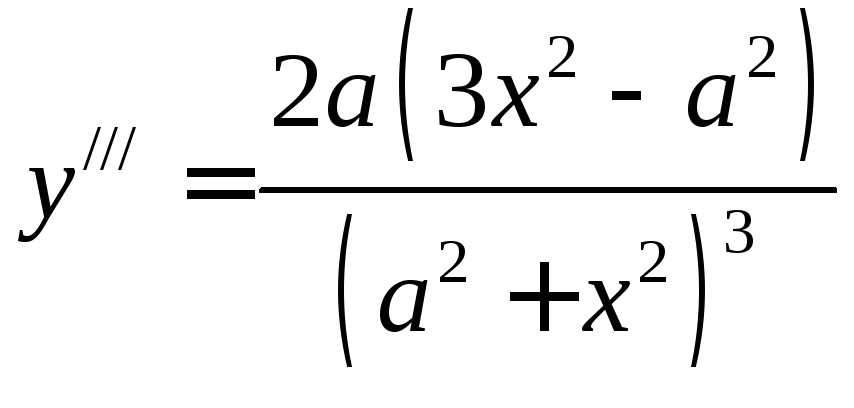 .
.
33.
![]() ,
,![]() -? Ответ:
-? Ответ:![]() .
.
34.
![]() ,
,![]() -?
-?
Ответ:
 ,
где
,
где![]() .
.
35.
![]() ,
,![]() -? Ответ:
-? Ответ:![]() .
.
36.
![]() ,
,![]() -? Ответ:
-? Ответ: .
.
37.
![]() ,
,![]()
![]() -? Ответ:
-? Ответ: .
.
38.
![]() ,
,![]() -?
-?
Ответ:
![]() ,
где
,
где![]() ,
,![]() .
.
39.
![]() ,
,![]() -?
-?
Указание:
Преобразовать выражение к виду:
![]() .
.
По формуле п. 36
 и
и
 .
.
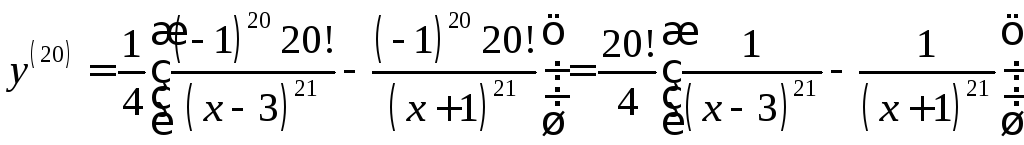 .
.
40.
![]() ,
,![]() - ? Ответ:
- ? Ответ:![]() .
.
Указание:
в формуле п. 38 положить
![]() .
.
42.
![]() ,
,![]() -? Ответ:
-? Ответ:![]() .
.
Указание:
в формуле п. 38 положить
![]() .
.
41.
![]() ,
,![]() -? Ответ:
-? Ответ:![]() .
.
Указание:
Находим первую производную
![]() .
.
По формуле п. 36
 .
.
43.
![]() ,
,![]() -?
-?
Указание:
Записать функцию в виде
![]() и, применяя формулу Лейбница,
продифференцироватьn
раз. При
и, применяя формулу Лейбница,
продифференцироватьn
раз. При
![]() будем иметь
будем иметь
![]() .
Откуда при
.
Откуда при![]() получим
получим![]() или
или![]() .
Полученная рекуррентная формула
позволяет определить
.
Полученная рекуррентная формула
позволяет определить
![]() -
ую производную в точке
-
ую производную в точке
![]()
![]() .
Значения
.
Значения![]() находятся непосредственно
находятся непосредственно
![]() ,
,
 .
.
![]() ,
,
![]() .
.
44.
![]() ,
,![]() -? Ответ:
-? Ответ:![]() .
.
45.
![]() .
.
