15. Варианты типового расчета

1 вариант

1. Найти наибольшее и наименьшее значения функции

а отрезке

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Какие размеры должен иметь прямой круговой цилиндр, поверхность которого равна , чтобы его объем был наибольшим?

2 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Доказать, что из всех прямоугольников, имеющих данный периметр , наибольшую площадь имеет квадрат.

3 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Доказать, что из всех прямоугольников, имеющих данную площадь , квадрат имеет наименьший периметр.

4 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Консервная банка объемом должна иметь цилиндрическую форму с дном и крышкой. Каково должно быть отношение диаметра основания цилиндра к его высоте, чтобы на изготовление банки пошло наименьшее количество жести?

5 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. В равнобедренный треугольник с основанием 20 см и высотой 8 см вписан прямоугольник, одна из сторон которого лежит на основании треугольника. Какова должна быть высота прямоугольника, чтобы он имел наибольшую площадь?

6 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Полотняный шатер объемом имеет форму прямого кругового конуса. Каково должно быть отношение высоты конуса к радиусу основания, чтобы на шатер ушло наименьшее количество полотна.

7 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики:

a) 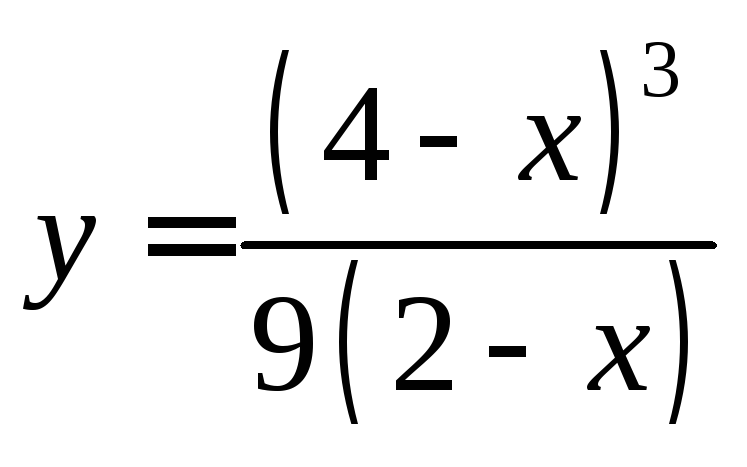;b) .

3. В прямоугольный треугольник с гипотенузой 10 см и углом в 30вписан прямоугольник, основание которого расположено на гипотенузе. Каковы должны быть размеры этого прямоугольника, чтобы его площадь была наибольшей?

8 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Требуется изготовить коническую воронку с образующей L. Какова должна быть высота воронки, чтобы вместимость ее была наименьшей?

9 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Определить размеры прямого открытого бассейна объемом 32 мс квадратным дном так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.

10 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Найти высоту прямого кругового конуса наименьшего объема, описанного около полушара радиусатак, чтобы центр основания конуса лежал в центре шара.

11 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ; b) .

3. Найти прямоугольный треугольник наибольшей площади, имеющий гипотенузой отрезок .

12 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Сопротивление балки прямоугольного поперечного сечения на сжатие пропорционально площади этого сечения. Каковы должны быть размеры сечения балки, вырезанной из круглого бревна диаметром , чтобы ее сопротивление на сжатие было наибольшим?

13 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Чтобы по возможности уменьшить трение жидкости о стенки канала, площадь, стачиваемая водой, должна быть, возможно, меньшей. Показать, что лучшей формой открытого прямоугольного канала с заданной площадью поперечного сечения является такая, при которой ширина канала превышает вдвое его высоту.

14 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. На оси параболы дана точка на расстоянииот вершины. Найти абсциссу ближайшей к ней точки кривой.

15 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Найти высоту прямого кругового цилиндра с наибольшим объемом, который может быть вписан в шар радиуса .

16 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Найти высоту прямого кругового конуса с наименьшим объемом, описанного около шара радиуса .

17 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Какова должна быть сторона основания правильной треугольной призмы данного объема , чтобы полная поверхность призмы была наименьшей?

18 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. На прямой, соединяющей два источника света, найти наименее освещенную точку, если силы света источников относятся как 64:27, а расстояние между ними равно 35 см.

19 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. В прямоугольной системе координат через точку (1;2) проведена прямая с отрицательным угловым коэффициентом, которая вместе с осями координат образует треугольник. Каковы должны быть отрезки, отсекаемые прямой на осях координат, чтобы площадь треугольника была наименьшей?

20 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Стрела прогиба балки прямоугольного поперечного сечения обратно пропорциональна произведению ширины этого сечения на куб его высоты. Каковы должны быть размеры сечения балки, вырезанной из круглого бревна диаметром , с наименьшей стрелой прогиба (наибольшей жесткости)?

21 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. В прямоугольной системе координат через точку (1;4) проведена прямая, пересекающаяся с положительными полуосями координат. Написать уравнение прямой, если сумма отрезков, отсекаемых ею на осях координат, принимает наименьшее значение.

22 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Сопротивление балки прямоугольного поперечного сечения на изгиб пропорционально произведению ширины этого сечения на квадрат его высоты. Каковы должны быть размеры сечения балки, вырезанной из круглого бревна диаметром , чтобы ее сопротивление на изгиб было наибольшим?

23 вариант

1. Найти наибольшее и наименьшее значения функции

на отрезке .

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Требуется устроить площадку в форме равнобедренного треугольника так, чтобы с двух сторон она была ограничена проволочной сеткой, а третья сторона (основание треугольника) примыкала к длинной каменной стене. Найти размеры треугольника наибольшей площади, если имеется 100 погонных метров сетки.

24 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Требуется сделать открытый сверху желоб, поперечное сечение которого имеет форму равнобочной трапеции, а дно и бока имеют ширину по 100 см. Какова должна быть ширина желоба наверху, чтобы он вмещал наибольшее количество воды?

25 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики:

a) ;b) .

3. Требуется изготовить цилиндрический сосуд заданного объема , открытый сверху. Определить его радиус и высоту так, чтобы поверхность была наименьшей.

26 вариант

1. Найти наибольшее и наименьшее значения функции на отрезке.

2. Провести полное исследование функций и построить их графики: a) ;b) ; с).

3. Найти высоту прямого кругового конуса с наименьшим объемом, описанного около шара радиуса R.

64