12. Направление выпуклости кривой. Точки перегиба

График функции называетсявыпуклым на интервале , если он расположен ниже любой своей касательной, проведенной в любой точке этого интервала. График функцииназываетсявогнутым, интервале , если он расположен выше любой своей касательной, проведенной в любой точке этого интервала. Точкаграфика функции, отделяющая его выпуклую часть от вогнутой части, называется точкой перегиба.

Достаточные условия выпуклости (вогнутости) графика функции. Если в интервале, то график функции является выпуклым в этом интервале. Если, то в этом интервале график функции вогнутый.

В точке перегиба графика функции вторая производная равна нулю или не существует. Точки, в которых вторая производная равна нулю или не существует, называются критическими точками второго рода. Если в некоторой точке, бесконечна или вовсе не существует именяет знак при переходе через точку, то график функции в точкеимеет перегиб. Еслисохраняет знак, то перегиба нет.

Найти интервалы выпуклости и точки перегиба функции:

1. .

Ответ: выпукла на ;

вогнута на ; очки перегиба.

2. .

Ответ: выпукла на ;

вогнута на ; точка перегиба.

3. .

Ответ: выпукла на ;

вогнута на ; точек перегиба нет.

4. .

Ответ: выпукла на ;

вогнута на ; точки перегиба.

5. .

Ответ: выпукла на ;

вогнута на ; точка перегиба.

6. .

Ответ: выпукла на ;

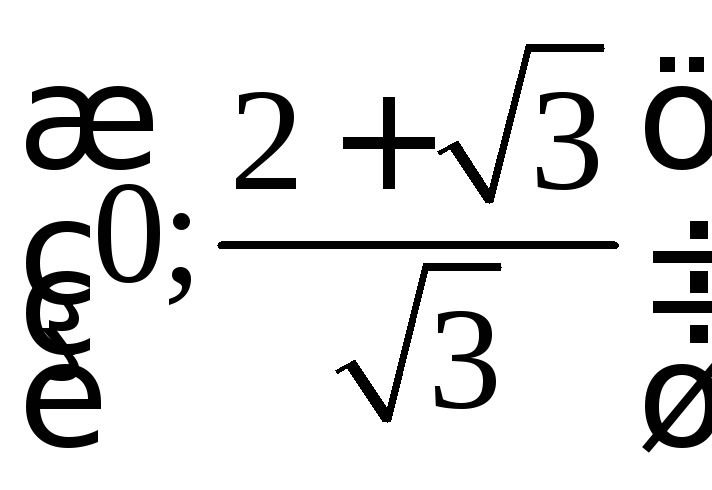вогнута на ; точка перегиба.

7. .

Ответ: выпукла на ;

вогнута на ; точки перегиба.

8. .

Ответ: выпукла на ;

вогнута на ; точки перегиба.

9. .

Ответ: выпукла на ;

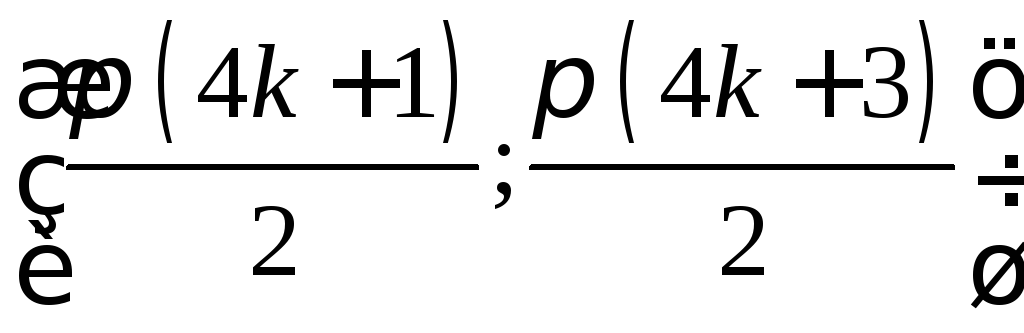вогнута на ; точки перегиба,.

10. .

Ответ: выпукла на ;

вогнута на ; точки перегиба.

11. .

Ответ: выпукла на ;

вогнута на ; точки перегиба.

12. .

Ответ: выпукла на ;

вогнута на ; точки перегиба.

13. .

Ответ: выпукла на ;

вогнута на ; точки перегиба.

14. .

Ответ: выпукла на ;

вогнута на ; точки перегиба.

15. . Ответ: выпукла на;

вогнута на ; точек перегиба нет.

16. . Ответ: выпукла на;

вогнута на , точка перегиба.

17. . Ответ: точка перегиба.

18. . Ответ: точка перегиба.

19. . Ответ: точка перегиба.

20. При каких значениях параметра функцияимеет точки перегиба? Ответ:.

21. Доказать, что график функции имеет точки перегиба, лежащие на одной прямой.

22. Доказать, что точки перегиба графика функции лежат на кривой.

23. Может ли точка перегиба функции быть ее точкой экстремума?

24. Может ли всюду выпуклая (вогнутая) функция иметь более одного экстремума?

Доказать неравенство:

25. .

26. .

27. .

28. .

29. .

30. .

31. .