
Министерство образования и науки РФ
ГОУ ВПО «Алтайский государственный технический университет им И.И, Ползунова»
Москаленко Е.М
Статика
Методические указания и варианты заданий по дисциплине
«Механика и технологии» для студентов специальности «Инноватика»
Барнаул 2012
-
Основные понятия и законы статики
Сила- векторная величина характеризуемая: 1- модулем силы; 2- точкой приложения; 3- направлением.
Пара сил- система двух параллельных, равных и направленных в противоположные стороны сил. Плоскость, проходящая через силы, составляющие пару называется плоскостью действия пары.
Пара силы характеризуется:
-
моментом пары сил;
-
плоскостью действия;
-
направлением момента;
Приложенную к абсолютно твёрдому телу силу можно переносить вдоль линии её действия в любую точку.
Силу, приложенную к абсолютно твёрдому телу, можно переносить в плоскости её действия в любую точку тела, прибавляя при этом пару сил с моментом, равным моменту силы относительно переносимой точки.
Пару сил, не изменяя оказываемого ей действия можно переносить куда угодно в плоскости действия пары.
Теорема о приведении системы сил к данному центру.
Любая система сил, действующая на абсолютно твёрдое тело, может быть приведена к произвольно выбранному центру в виде главного вектора R и лавного момента М.
Для
равновесия любой системы сил необходимо
и достаточно чтобы главный вектор и
главный момент системы были равны нулю,
т.е. чтобы выполнялось условие ![]() .
.
Сила может быть распределена по площади и по длине.
В том случае, если размеры площади, по которой распределена сила малы по сравнению с размерами тела, считаем, что сила приложена в одной точке (сосредоточенная сила).
Распределённые силы характеризуются интенсивностью, т.е. величиной силы, приходящейся на единицу площади или длины.



 В
рамках данной работы мы будем иметь
дело с силой, распределенной по длине,
которую можно заменить одной сосредоточенной
силой приложенной в середине участка
и равной произведению интенсивности
на длину участка (см. рис. 1).
В
рамках данной работы мы будем иметь
дело с силой, распределенной по длине,
которую можно заменить одной сосредоточенной
силой приложенной в середине участка
и равной произведению интенсивности
на длину участка (см. рис. 1).

Рисунок 1.
-
Плоская система сил.
Плоскими системы сил называются в том случае, если все силы и моменты пар сил расположены в одной плоскости. По расположению сил на плоскости они классифицируется следующим образом:
-
Система сходящихся сил(сил, пересекающихся в одной точке).
-
Система параллельных сил.
-
Система произвольно расположенных сил.
-
Система сходящихся сил (см. рис. 2).
 Рисунок 2. Где n
– целое положительное число.
Для
такой системы сил можно записать два
независимых уравнения равновесия: 1.
Рисунок 2. Где n
– целое положительное число.
Для
такой системы сил можно записать два
независимых уравнения равновесия: 1.
 2.
2. 
-
Система параллельных сил (см. рис. 3).
 Рисунок. 3. Где n
– целое положительное число.
Все
силы, образующие систему параллельны
друг другу, ось y
параллельна силам системы.
Для такой системы можно составить два
независимых уравнения равновесия. 1
вариант:
Рисунок. 3. Где n
– целое положительное число.
Все
силы, образующие систему параллельны
друг другу, ось y
параллельна силам системы.
Для такой системы можно составить два
независимых уравнения равновесия. 1
вариант: 
 2 вариант:
2 вариант: 
 Точки А и В не должны лежать на одной
прямой параллельной силам системы.
Точки А и В не должны лежать на одной
прямой параллельной силам системы.
-
Система произвольно расположенных сил (см. рис. 4). Mm M1
 Рисунок. 4. Где n
и m
– целые положительные числа.
для
такой системы можно составить 3
независимых уравнения равновесия
1вариант: 1
Рисунок. 4. Где n
и m
– целые положительные числа.
для
такой системы можно составить 3
независимых уравнения равновесия
1вариант: 1  2
2  3
3 2
вариант: 1
2
вариант: 1
 2
2  3
3 3
вариант: 1
3
вариант: 1
 2
2
 3
3
Условно считаем проекцию силы на ось положительной, если направление проекции силы совпадает с направлением оси.
Условно считаем момент силы относительно точки положительным, если тело, закреплённое в этой точке стремится повернуться против часовой стрелки.
Момент пары сил направленный против часовой стрелки считаем положительным.
В противных случаях проекцию силы на ось, момент силы, относительно точки и момент пары сил считаем отрицательным.
-
Реакция связей. Типы опор балок и рам.
Устройства, ограничивающие перемещение тела в пространстве, называют связями. Сила, с которой связь действует на тело называется реакцией связи.
Для плоских балок и рам используют 3 типа опор:
Жёсткое защемление или заделка. (см. рис. 5). Такая опора обладает тремя связями. Отсутствуют перемещения в
г оризонтальном
и вертикальном, направлениях и угловое.
оризонтальном
и вертикальном, направлениях и угловое.
Рисунок 5.
Шарнирно неподвижная опора (см. рис. 6).
Т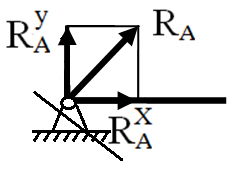 акая
опора обладает двумя связями. Отсутствуют
перемещения в горизонтальном и
вертикальном направлении.
акая
опора обладает двумя связями. Отсутствуют
перемещения в горизонтальном и
вертикальном направлении.
Рисунок 6.
Шарнирно подвижная опора (см. рис. 7). Такая опора обладает одной связью. Перемещение по нормали к опорной поверхности равно нулю.
 Рисунок 7.
Рисунок 7.
Для вычисления реакции связей составляют уравнения равновесия. Если количество независимых уравнений равновесия позволяют вычислить неизвестные величины, то задача является статистически определимой.
