ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Математический факультет

Кафедра алгебры и математической логики

МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ

Варианты заданий для самостоятельной работы студентов

Барнаул 2010

Составитель: к. ф.-м. н. С.А. Шахова

Рецензент: д. ф.-м. н. А.И. Будкин

Методические указания содержат варианты заданий для самостоятельной работы студентов по теме «Матрицы и определители», изучаемой в курсе линейной алгебры. Предназначены для студентов первого курса математического факультета.

Вариант 1.

1. Вычислить , где,,.

2. Найти все матрицы, перестановочные с матрицей .

3. Найти для всех натуральных значений.

4. Перемножить матрицы а) 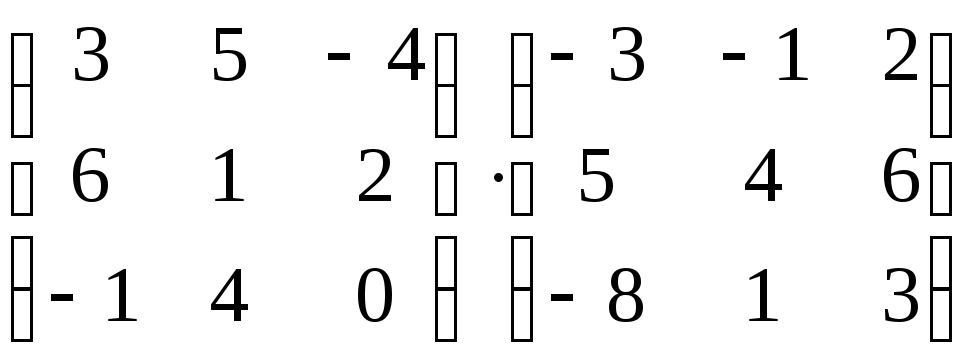; б).

5. Вычислить определители а) ; б); в); г).

6. Найти обратную матрицу к матрице , а) выражая один столбец неизвестных через другой; б) по формуле обратной матрицы.

7. Решить матричное уравнение .

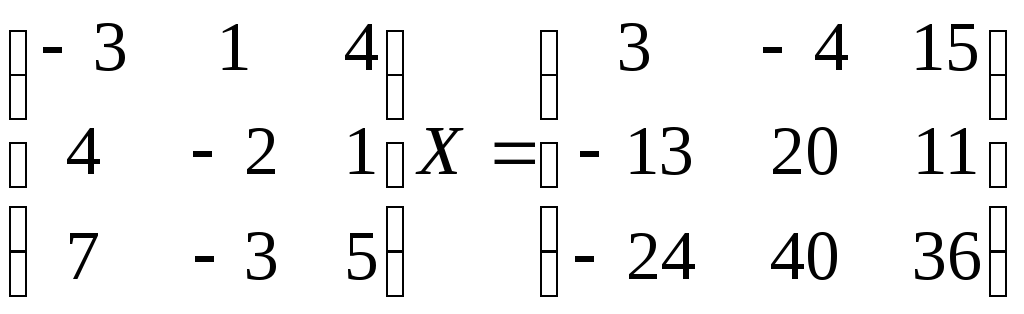8. Решить систему линейных уравнений а) методом Гаусса; б) с помощью обратной матрицы, записав систему в матричном виде; в) по формулам Крамера.

9. Представить матрицу-строку в виде линейной комбинации строк,,.

Вариант 2.

1. Вычислить , где,,.

2. Найти все матрицы, перестановочные с матрицей .

3. Найти для всех натуральных значений.

4. Перемножить матрицы а) ; б).

5. Вычислить определители а) ; б); в); г).

6. Найти обратную матрицу к матрице , а) выражая один столбец неизвестных через другой; б) по формуле обратной матрицы.

7. Решить матричное уравнение .

8. Решить систему линейных уравнений а) методом Гаусса; б) с помощью обратной матрицы, записав систему в матричном виде; в) по формулам Крамера.

9. Представить матрицу-строку в виде линейной комбинации строк,,.

Вариант 3.

1. Вычислить , где,,.

2. Найти все матрицы, перестановочные с матрицей .

3. Найти для всех натуральных значений.

4. Перемножить матрицы а) ; б).

5. Вычислить определители а) ; б); в); г).

6. Найти обратную матрицу к матрице , а) выражая один столбец неизвестных через другой; б) по формуле обратной матрицы.

7. Решить матричное уравнение .

8. Решить систему линейных уравнений а) методом Гаусса; б) с помощью обратной матрицы, записав систему в матричном виде; в) по формулам Крамера.

9. Представить матрицу-строку в виде линейной комбинации строк,,.

Вариант 4.

1. Вычислить , где,,.

2. Найти все матрицы, перестановочные с матрицей .

3. Найти для всех натуральных значений.

4. Перемножить матрицы а) ; б).

5. Вычислить определители а) ; б); в); г).

6. Найти обратную матрицу к матрице , а) выражая один столбец неизвестных через другой; б) по формуле обратной матрицы.

7. Решить матричное уравнение .

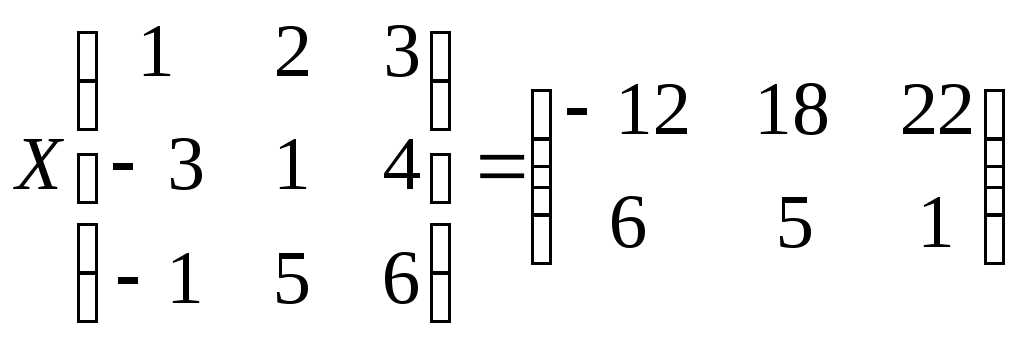8. Решить систему линейных уравнений а) методом Гаусса; б) с помощью обратной матрицы, записав систему в матричном виде; в) по формулам Крамера.

9. Представить матрицу-строку в виде линейной комбинации строк,,.

Вариант 5.

1. Вычислить , где,,.

2. Найти все матрицы, перестановочные с матрицей .

3. Найти для всех натуральных значений.

4. Перемножить матрицы а) ; б).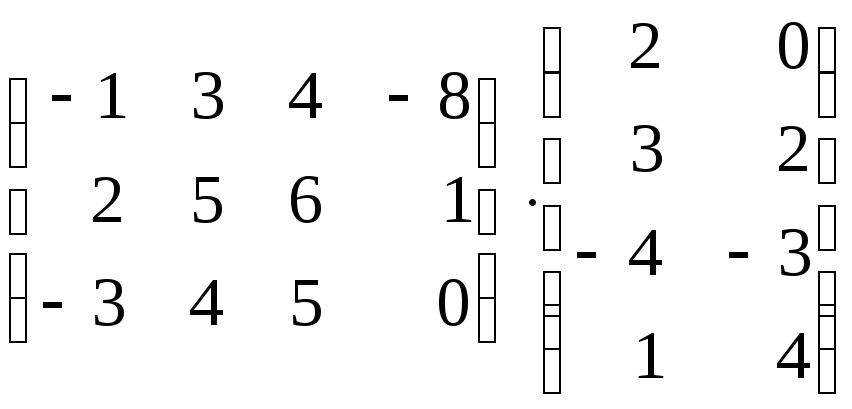

5. Вычислить определители а) ; б); в); г).

6. Найти обратную матрицу к матрице , а) выражая один столбец неизвестных через другой; б) по формуле обратной матрицы.

7. Решить матричное уравнение .

8. Решить систему линейных уравнений 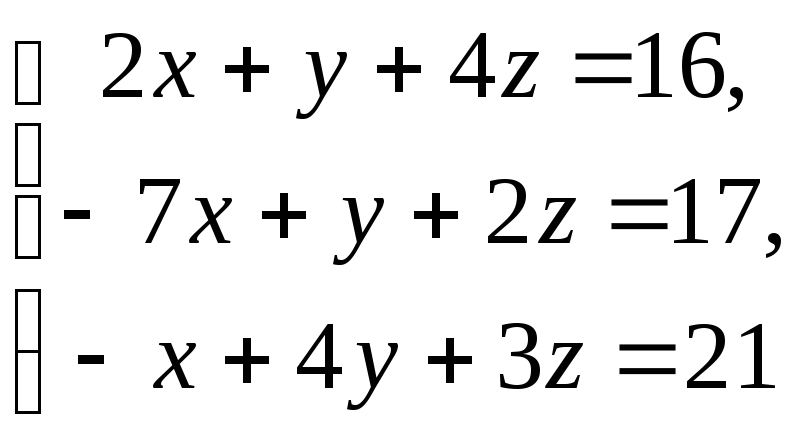а) методом Гаусса; б) с помощью обратной матрицы, записав систему в матричном виде; в) по формулам Крамера.

9. Представить матрицу-строку в виде линейной комбинации строк,,.

Вариант 6.

1. Вычислить , где,,.

2. Найти все матрицы, перестановочные с матрицей .

3. Найти для всех натуральных значений.

4. Перемножить матрицы а) ; б).

5. Вычислить определители а) ; б); в); г).

6. Найти обратную матрицу к матрице , а) выражая один столбец неизвестных через другой; б) по формуле обратной матрицы.

7. Решить матричное уравнение .

8. Решить систему линейных уравнений а) методом Гаусса; б) с помощью обратной матрицы, записав систему в матричном виде; в) по формулам Крамера.

9. Представить матрицу-строку в виде линейной комбинации строк,,.