
6.1. Производная, её геометрический и физический смысл
Дифференцирование функции – вычисление производной.
Дифференцируемая функция – функция, у которой есть производная.
|
Определение
производной.
|
|
|
|
Г |
|
|
|
|
Уравнение
касательной
к графику функции
Уравнение
нормали
к графику функции
Нормаль
Угол между
кривыми
|
|
|
|
|
|
|
Физический
смысл производной:
|
|
|
6.2 Вычисление производной. Дифференциал
I.
Правила дифференцирования.
![]() – дифференцируемые функции
– дифференцируемые функции
-
Константа:
 ;
; -
 ;
; -
Сумма (разность):
 ;
; -
Произведение:
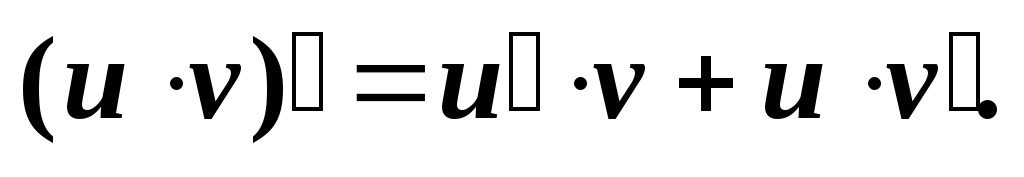
-
Константа умножить на функцию:
 ;
; -
Частное:
 ;
; -
Константа разделить на функцию:
 .
.
|
II. Таблица производных |
||||||
|
Степенные функции
Показательные функции
Логарифмические функции
|
Тригонометрические функции
Гиперболические функции
|
Обратные тригонометрические функции
|
||||
|
Производные высших порядков |
||||||
|
Вторая
производная
n-ая
производная
|
||||||
|
Производные параметрически заданной функции
|
||||||
|
Дифференциал
|
||||||
|
|
|
|||||
|
||||||
|
Погрешности вычисления
Найти
|
||||||
|
6.3 Теоремы о среднем. Правило Лопиталя |
||||||
|
|
Теорема
Ролля.
Функция
Тогда
существует по крайней мере одна точка
Геометрический
смысл:
касательная к графику функции в точке
|
|
||||
|
|
Теорема
Лагранжа.
Функция
Тогда
существует по крайней мере одна точка
Геометрический
смысл:
касательная к графику функции в точке
|
|
||||
|
Теорема
Коши. Функции
Тогда
существует по крайней мере одна точка
|
|
|||||
|
Раскрытие неопределённостей в пределах |
|
|||||
|
Правило
Лопиталя.
Функции
|
|
|||||
|
Раскрытие других видов неопределенностей |
|
|||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
Формула Тейлора.
Функция
где
Формула Маклорена:
|
|
|||||

 еометрический
смысл производной:
значение производной функции
еометрический
смысл производной:
значение производной функции

 .
.


