
- •Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •Вариант № 9
- •Вариант № 10
- •Вариант № 11
- •Вариант № 12
- •Вариант № 13
- •Вариант № 14
- •Вариант № 15
- •Вариант № 16
- •Вариант № 17
- •Вариант № 18
- •Вариант № 19
- •Вариант № 20
- •Вариант № 21
- •Вариант № 22
- •Вариант № 23
- •Вариант № 24
- •Вариант № 25
- •Вариант № 26
- •Вариант № 27
- •Вариант № 28
- •Вариант № 29
Вариант № 1
Даны две функции. Требуется:
выяснить, является функция алгебраической или трансцендентной;
найти область определения функции;
вычислить
 ;
;исследовать функцию на чётность, нечётность;
исследовать функцию на периодичность, если функция периодична, указать её наименьший период;
найти нули функции и интервалы знакопостоянства;
исследовать функцию на непрерывность и найти вертикальные асимптоты;
исследовать поведение функции на бесконечности и найти её горизонтальные и наклонные асимптоты;
для второй из заданных функций построить график.
1.
![]() . 2.
. 2.![]() .
.
Решить задачу на составление аналитической функции.
Бревно длиной 20м имеет форму усечённого конуса, диаметры оснований которого равны соответственно2м и1м. Требуется вырубить из бревна балку с квадратным поперечным сечением, ось которой совпала бы с осью бревна. Выразить объём балки как функцию высоты балки.
Вычислить пределы:
-
1.
 .
.7.
 .
.2.
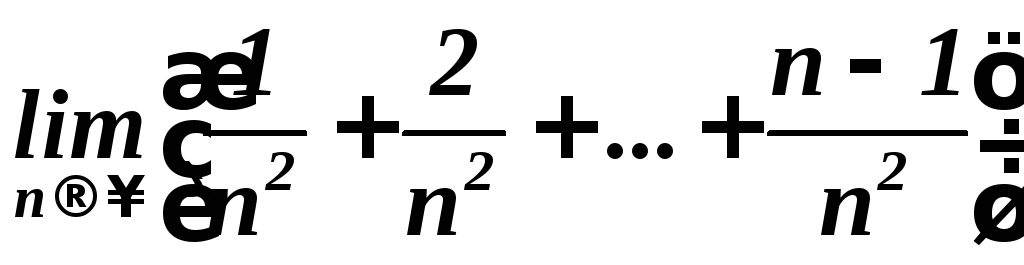 .
.8.
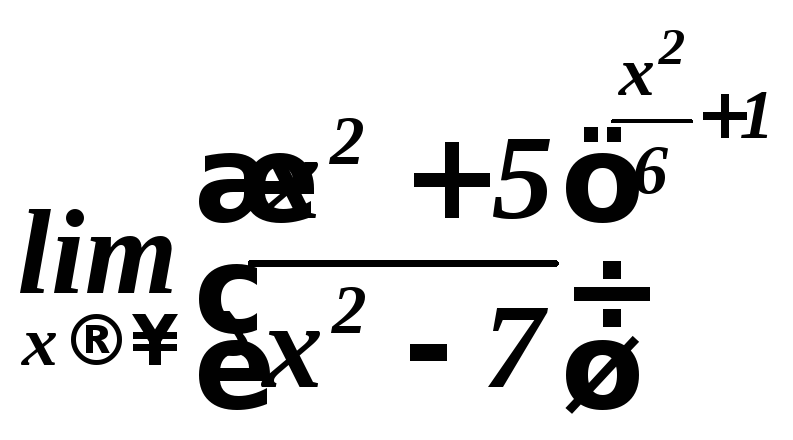 .
.3.
 .
.9.
 .
.4.
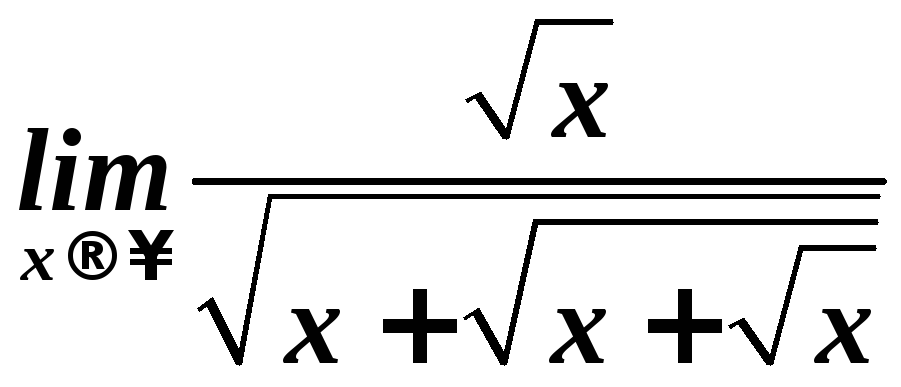 .
.10.
 .
.5.
 .
.11.
 .
.6.
 .
.12.
 .
.Вычислить односторонние пределы и предел этой же функции при
 .
.13.
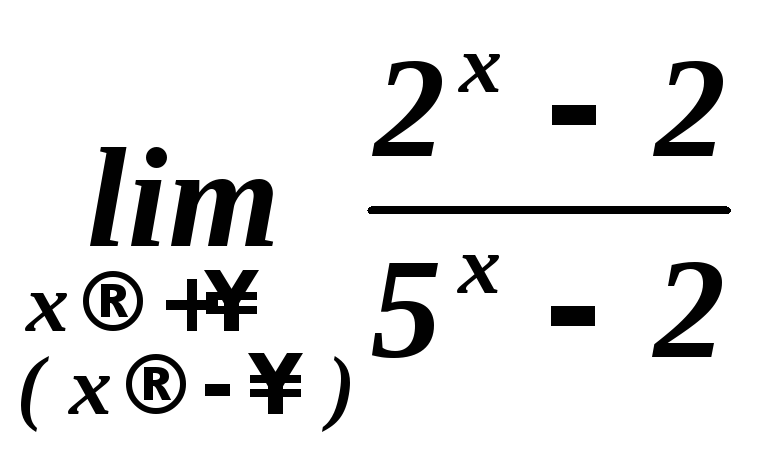 .
.
Используя определение непрерывности функции в точке через предел её приращения, доказать непрерывность функции
 в заданной точке
в заданной точке .
.Даны две функции. Исследовать функции на непрерывность, указать тип точек разрыва, сделать схематический чертёж графика функции.
1.
![]() . 2.
. 2.
По эскизу графика описать поведение функции на языке пределов в точках
 и
и и при стремлении аргумента функции к
и при стремлении аргумента функции к .
.

VII. Построить график
функции![]() ,
если известно, что
,
если известно, что
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Дать каждому из пределов определение по Коши (используя неравенства для задания - и-окрестностей).
Вариант № 2
Даны две функции. Требуется:
выяснить, является функция алгебраической или трансцендентной;
найти область определения функции;
вычислить
 ;
;исследовать функцию на чётность, нечётность;
исследовать функцию на периодичность, если функция периодична, указать её наименьший период;
найти нули функции и интервалы знакопостоянства;
исследовать функцию на непрерывность и найти вертикальные асимптоты;
исследовать поведение функции на бесконечности и найти её горизонтальные и наклонные асимптоты;
для второй из заданных функций построить график.
1.
 . 2.
. 2.![]() .
.
Решить задачу на составление аналитической функции.
Полоса железа шириной 10м и длиной20м должна быть согнута в виде открытого цилиндрического желоба (сечение желоба имеет форму кругового сегмента). Выразить объём желоба как функцию центрального угла, опирающегося на дугу сегмента.
Вычислить пределы:
-
1.
 .
.7.
 .
.2.
 .
.8.
 .
.3.
 .
.9.
 .
.4.
 .
.10.
 .
.5.
 .
.11.
 .
.6.
 .
.12.
 .
.Вычислить односторонние пределы и предел этой же функции при
 .
.13.
 .
.
Используя определение непрерывности функции в точке через предел её приращения, доказать непрерывность функции
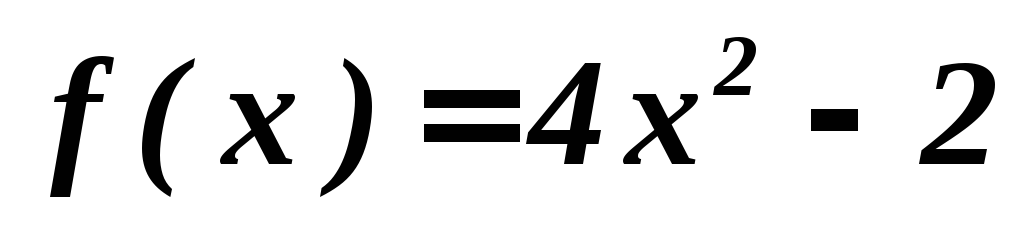 в заданной точке
в заданной точке .
.Даны две функции. Исследовать функции на непрерывность, указать тип точек разрыва, сделать схематический чертёж графика функции.
1.![]() . 2.
. 2.
По эскизу графика описать поведение функции на языке пределов в точках
 и
и и при стремлении аргумента функции к
и при стремлении аргумента функции к .
.

VII. Построить график
функции![]() ,
если известно, что
,
если известно, что
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Дать каждому из пределов определение по Коши (используя неравенства для задания - и-окрестностей).
