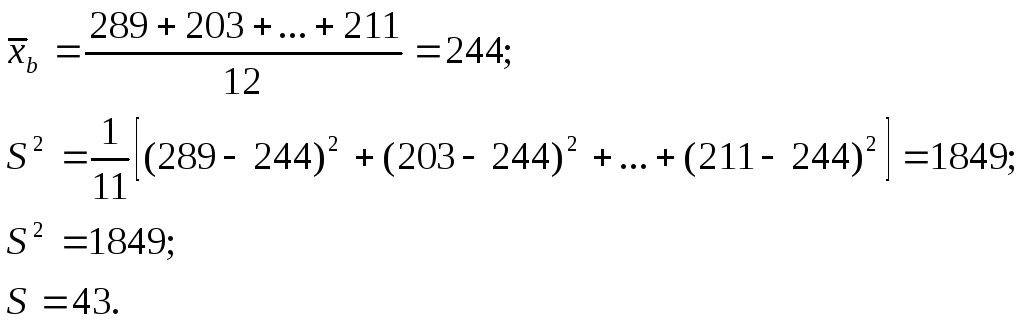- •Рязань 2009
- •Глава 1. Предел функции
- •1.1. Определение предела
- •1.2. Операции над пределами
- •1.3. Замечательные пределы
- •1.4. Примеры
- •1.5. Варианты заданий
- •1.6. Контрольные вопросы Глава 2. Производная и дифференциал
- •2.1 Понятие производной
- •2.2. Геометрический и физический смысл производной
- •2.3. Таблица производных
- •2.4. Основные правила дифференцирования
- •2.5. Производные высших порядков
- •2.6. Дифференциал функции
- •2.7. Геометрический смысл и свойства дифференциала
- •2.8. Дифференциалы высших порядков
- •2.9. Примеры
- •2.10. Варианты заданий
- •2.11. Контрольные вопросы
- •Глава 3. Исследование функций и построение графиков
- •3.1. Промежутки монотонности и знакопостоянства
- •3.2. Экстремумы функции
- •3.3. Выпуклость и вогнутость функции. Точка перегиба
- •3.4. Асимптоты
- •3.5.Общая схема исследования функции и построение графиков
- •3.6. Примеры
- •3.7. Варианты заданий
- •3.8. Контрольные вопросы
- •Глава 4. Функции нескольких переменных
- •4.1. Определение функции нескольких переменных
- •4.2. Частные производные
- •4.3. Полный дифференциал
- •4.5. Примеры
- •4.6. Варианты заданий
- •4.7. Контрольные вопросы Глава 5. Численное дифференцирование
- •5.1. Формулы для вычисления первой производной
- •5.2. Формулы второй производной
- •5.3. Примеры
- •5.4. Варианты заданий
- •5.5. Контрольные вопросы Глава 6 Основы интерполяции.
- •6.1. Постановка задачи
- •Интерполяционные формулы конечных разностей
- •6.3. Интерполяционные формулы центральных разностей
- •6.4. Интерполирование функции с не равноотстоящими узлами
- •6.5. Варианты заданий
- •6.6. Контрольные вопросы Глава 7. Неопределенный интеграл
- •7.1. Первообразная функция и неопределенный интеграл
- •7.2. Основные свойства неопределенного интеграла
- •7.3. Таблица простейших интегралов
- •7.4. Основные методы интегрирования
- •7.4.1. Непосредственное интегрирование
- •7.4.2. Метод подстановки (замена переменной)
- •7.4.3. Интегрирование по частям
- •7.5. Примеры
- •7.6. Варианты заданий
- •7.7. Контрольные вопросы
- •Глава 8. Определенный интеграл
- •8.1. Основные понятия и свойства определенного интеграла
- •Свойства определенного интеграла
- •8.2. Основные методы интегрирования
- •8.2.1. Формула Ньютона-Лейбница
- •8.2.2. Метод подстановки
- •8.2.3. Интегрирование по частям
- •8.3. Примеры
- •8.4. Варианты заданий
- •8.5. Биологические, физические и медицинские приложения определенного интеграла
- •8.5.1. Примеры задач прикладного характера.
- •8.5.2. Примеры решения задач.
- •8.5.3. Варианты заданий
- •Глава 9. Численное интегрирование
- •9.1. Формула прямоугольников
- •9.2. Формула трапеций
- •9.3. Метод средних
- •9.4. Формула Симпсона
- •9.5. Примеры
- •9.6. Варианты заданий
- •9.7. Контрольные вопросы
- •Глава 10. Дифференциальные уравнения
- •10.1. Основные определения
- •10.2. Уравнения с разделяющимися переменными
- •10.3. Однородные уравнения первого порядка
- •10.4. Линейные уравнения первого порядка
- •9.5. Примеры
- •I. Метод Лагранжа
- •II. Метод Бернулли
- •1) Метод вариации произвольной постоянной
- •2) Метод подстановки
- •10.6. Варианты заданий
- •10.7. Применение дифференциальных уравнений в биологии и медицине.
- •10.8. Варианты заданий
- •10.9. Контрольные вопросы
- •Глава 11. Численные методы решения дифференциальных уравнений
- •11.1. Метод Эйлера
- •10.2. Метод Рунге – Кутта
- •10.3. Примеры
- •11.4. Варианты заданий
- •11.4. Контрольные вопросы
- •Глава 12. Элементы теории вероятностей
- •12.1. Случайное событие
- •12.2. Комбинаторика
- •12.3. Вероятность случайного события
- •Закон сложения вероятностей
- •12.5. Варианты заданий
- •12.6. Условная вероятность, закон умножения вероятностей
- •12.7. Варианты заданий
- •12.8. Формулы полной вероятности и Байеса
- •12.9. Варианты заданий
- •11.10. Формулы Бернулли, Пуассона и Муавра-Лапласа
- •12.11. Варианты заданий
- •12.2. Случайные величины
- •12.2.1. Закон распределения случайной величины
- •12.2.2. Функция распределения случайных величин
- •12.2.3. Числовые характеристики дискретной случайной величины
- •12.2.4. Плотность вероятности непрерывных случайных величин
- •12.2.5. Нормальный закон распределения
- •12.3. Варианты заданий
- •Глава 13. Статистический анализ результатов исследований
- •13.1. Основные понятия математической статистики
- •13.1. Варианты заданий
- •13.2. Статистические оценки параметров распределения. Выборочные характеристики
- •13.2.1. Характеристики положения
- •13.2.2. Характеристики рассеяния вариант вокруг своего среднего
- •13.3. Варианты заданий
- •13.4. Оценка параметров генеральной совокупности по ее выборке
- •13.4.1. Точечная оценка параметров генеральной совокупности
- •13.5. Варианты заданий
- •13.6. Интервальная оценка параметров генеральной совокупности
- •13.7. Варианты заданий
- •1.8. Контрольные вопросы
- •Глава 14. Корреляционный и регрессионный анализ
- •14.1. Функциональная и корреляционная зависимости
- •14.2. Коэффициент линейной корреляции и его свойства
- •14.3. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции
- •14.4. Выборочное уравнение линейной регрессии. Метод наименьших квадратов
- •14.5. Нелинейная регрессия
- •14.6. Варианты заданий
- •Приложение
- •Критические значения выборочного коэффициента корреляции
- •Критерий Колмогорова – Смирнова Точные и асимптотические границы для верхней грани модуля разности истинной и эмпирической функции распределения
- •Распределение Пирсона (х2– распределение)
- •Распределение Фишера – Снедекора (f-распределение)
- •Библиографический список
- •Содержание
- •Глава 13. Статистический анализ результатов исследований 160
- •Глава 14. Корреляционный и регрессионный анализ 180
13.4.1. Точечная оценка параметров генеральной совокупности
Точечная оценка – это оценка, которая определяется одним числом. И это число определяется по выборке. Это функция результатов выборки, и она является точечной оценкой генерального параметра, т. е. принимает только одно значение.
Качество оценки устанавливается по трем свойствам: быть состоятельной, эффективной и несмещенной.
Точечная оценка называется состоятельной, если при увеличении объема выборки выборочная характеристика стремится к соответствующей характеристике генеральной совокупности.
Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками.
Точечную оценку называют несмещенной, если ее математическое ожидание равно оценивающему параметру при любом объеме выборки.
Несмещенной
оценкой генеральной средней
(математического ожидания) служит
выборочная средняя
![]() :
:
![]()
где
![]() - варианты выборки;
- варианты выборки;![]() - частота встречаемости вариант
- частота встречаемости вариант![]() ;n
- объем выборки.
;n
- объем выборки.
Выборочная
средняя является несмещенной оценкой
генеральной средней, так как
![]() ,т.е.
она эквивалентна истинной средней в
генеральной совокупности (популяции).
,т.е.
она эквивалентна истинной средней в
генеральной совокупности (популяции).
Выборочная
дисперсия
![]() не обладает свойством несмещенности.
Это смещенная оценка генеральной
дисперсии
не обладает свойством несмещенности.
Это смещенная оценка генеральной
дисперсии
![]() .
.
![]() -
это и означает, что выборочная дисперсия
-
это и означает, что выборочная дисперсия
![]() является смещенной оценкой
является смещенной оценкой
![]()
На
практике используют исправленную
выборочную дисперсию
![]() ,
которая является несмещенной оценкой
дисперсии генеральной совокупности:
,
которая является несмещенной оценкой
дисперсии генеральной совокупности:

Кроме того, в расчетах используют S - исправленное среднее квадратическое отклонение, называемое стандартным отклонением в выборке и ошибку выборочной средней
(стандартную
ошибку средней)
![]() :
:
![]() которая
отражает точность оценки.
которая
отражает точность оценки.
Стандартная ошибка уменьшится, т. е. оценка станет более точной, если объем выборки n увеличится и данные имеют небольшое рассеяние S.
Рассмотрим
разницу между S - стандартным отклонением
в выборке и
![]() - стандартной ошибкой среднего.
- стандартной ошибкой среднего.
На первый взгляд, они очень схожи, но их используют в разных целях. Среднее квадратическое отклонение S отражает вариабельность в значениях данных, и его указывают, если надо пояснить изменчивость в наборе данных, разброс данных.
Ошибка
выборочной средней
![]() характеризует точность выборочного
среднего
характеризует точность выборочного
среднего![]() и должна быть указана, если интерес
представляет среднее значение выборки.
и должна быть указана, если интерес
представляет среднее значение выборки.
Из генеральной совокупности извлечена выборка объема n=50.
|
|
2 |
5 |
10 |
7 |
|
|
16 |
12 |
8 |
14 |
Найти несмещенную оценку генеральной средней.
Решение:
![]()
По
выборке объема 30 найдена смещенная
оценка
![]() = 3 генеральной дисперсии. Найти
несмещенную оценку дисперсии генеральной
совокупности.
= 3 генеральной дисперсии. Найти
несмещенную оценку дисперсии генеральной
совокупности.
Решение:
Эта несмещенная оценка равна исправленной дисперсии:
![]()
Найти несмещенную оценку генеральной средней, дисперсии генеральной совокупности и стандартное отклонение по выборке объема 12, описывающую продолжительность в секундах физической нагрузки до развития приступа стенокардии:
289,203,359,243,232,210,251,251,246,224,239,220,211.
Решение: