1.2 Регенеративное усиление

Схему генератора, содержащего LC-контур, можно заменить эквивалентной схемой, содержащей активное и отрицательное сопротивления. При этом эквивалентное сопротивление контура определяется как

Величина отрицательного сопротивления зависит от параметров элементов схемы и глубины положительной обратной связи. Если обратная связь больше критической , имеет место генерация синусоидальных колебаний. Если обратная связь меньше критической, что соответствует условию, схема генератора (рисунок 1) находится в недовозбужденном режиме. В этом случае ее называютпотенциально автоколебательной.

Эквивалентное сопротивление потерь контура можно сделать очень малым, установив обратную связь близкой к критической так, чтобы схема «находилась» у порога генерации .

Рисунок 1– Эквивалентная схема автономной колебательной системы.

Рисунок 2 - Эквивалентная схема регенерированного контура, находящегося под внешним воздействием.

Схема, с положительной обратной связью, благодаря которой частично компенсируются потери в колебательном контуре, называется регенеративной, а контур – регенерированным.

При резонансном воздействии регенеративную схему можно использовать как усилитель. С уменьшением сопротивления добротность контура (рисунок 2) и напряжение на нем повышаются. Повышение добротности приводит к сужению полосы пропускания регенерированного контура. Рассмотрим стационарный режим в регенерированном контуре на примере схемы, изображенной на рисунке 3. Данная схема отличается от схемы автогенератора сLC-контуром в цепи затвора транзистора с трансформаторной связью только наличием внешнего генератора напряжения – сигнала . Из теории следует, что изображенное на рисунке 2 отрицательное сопротивление определяется из схемы 3 формулой:

, (1)

где М – коэффициент взаимной индуктивности, S_ср – средняя крутизна вольтамперной характеристики (ВАХ) транзистора, С – емкость конденсатора. Тогда эквивалентное активное сопротивление контура этой схемы имеет вид

Рисунок 3 – Схема регенератора на полевом транзисторе.

Найдем выражение для добротности регенерированного контура. Известно, что добротность обычного контура

, (2)

где ρ - характеристическое сопротивление контура. Добротность регенерированного контура определяется аналогично:

(3)

и всегда больше . Легко видеть, что добротностьрастет вместе с приближениемк, т.е. с приближением колебательного контура к порогу генерации. Усиление напряжения сигнала происходит за счет энергии, возвращаемой по цепи положительной обратной связи.

Для оценки получаемого при этом выигрыша в усилении вводится коэффициент регенерации. Он равен отношению напряжений на конденсаторе регенерированного к напряжению на конденсаторенерегенерированного контуров при воздействии гармонического сигнала, частота которого совпадает с резонансной частотой контура.

В рассматриваемой схеме (рисунок 3) напряжение на конденсаторе совпадает с напряжением на затворе транзистора, поэтому коэффициент регенерации можно записать в виде

.

При резонансе

,

где – амплитуда входного сигнала. Тогдакоэффициент регенерации можно выразить через отношение добротностей регенерированного и нерегенерированного контуров:

.

Выясним зависимость коэффициента регенерации от параметров схемы. Если схема работает в установившимся режиме, то можно воспользоваться формулой (3), определяющей добротность, и (1) для отрицательного сопротивления. В результате получим, что

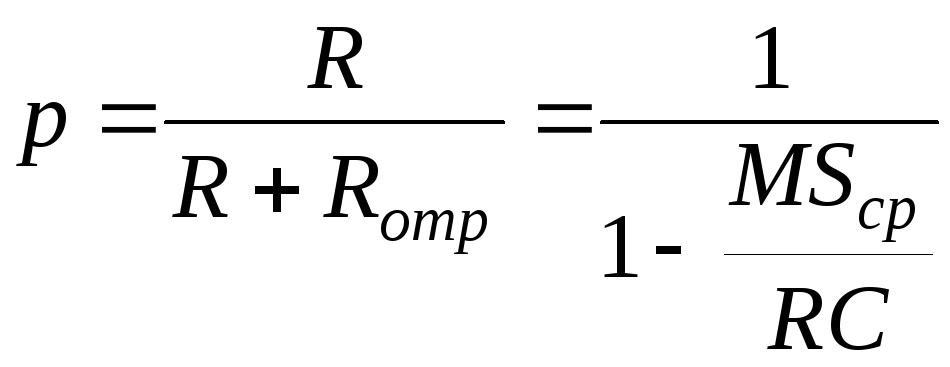
Средняя крутизна ВАХ транзистора зависит от амплитуды напряжений, действующих на затворе транзистора. Следовательно, коэффициент регенерации определяется не только параметрами схемы, но и напряжением сигнала.

Для выяснения количественной стороны этих закономерностей будем аппроксимировать ВАХ транзистора. Если рабочая точка находится в середине прямолинейного участка характеристики, то при аппроксимации значение определяется выражением

.

Подставив выражение средней крутизны характеристики в формулу, определяющую коэффициент регенерации, получим

, (4)

где – параметр самовозбуждения.

Для слабых сигналов, . Тогда выражение для коэффициента регенерации упрощается и принимает вид:

(5)

Зависимость изображена на рисунке 4.

Рисунок 4 – Зависимость коэффициента регенерации от параметра самовозбуждения при слабых сигналах

Видно, что коэффициент регенерации увеличивается по мере приближения к 1. У границы самовозбуждения, т.е. при, коэффициентрезко возрастает. Отсюда следует, что при большом усилении незначительное изменение режима может вызвать генерацию, что нарушит нормальную работу схемы, работающей в качестве усилителя.

Необходимо отметить, что рисунок 4 служит качественной иллюстрацией найденной зависимости, т.е. правильно передает только основные черты закономерности. Действительно, в основу вывода зависимости (5) было положено условие малости амплитуды напряжения на затворе транзистора.

В то же время с ростом растет усиление; следовательно, растет и амплитуда напряженияи в этом случае исходное предположение оказывается несправедливым.

Вернемся к (4) и рассмотрим зависимость коэффициента регенерации от амплитуды напряжения на затворе транзистора. Исследование проведем отдельно для малых и больших амплитуд. При малых амплитудах значение определяется (5), а при больших () — выражением

.

Видно, что полученное выражение стремится к единице с ростом напряжения . Зависимостьпри фиксированном значении параметра самовозбужденияимеет вид, соответствующий рисунку 5.

Из рисунка 5 видно, что при помощи регенератора эффективно можно усиливать только слабые сигналы: для сильных сигналов регенеративное усиление неэффективно. Объясняется это тем, что средняя крутизна характеристики падает с ростом амплитуды напряжения на затворе транзистора. При этом по цепи положительной обратной связи меньше возвращается энергии, в меньшей степени компенсируются потери.

Рисунок 5 – Зависимость коэффициента регенерации от амплитуды напряжения на затворе транзистора.

Рассмотрим теперь вопрос о влиянии положительной обратной связи на форму резонансной кривой регенерированного контура. Выражение приведенной резонансной кривой для нерегенерированного контура имеет вид:

,

где: (I – значение силы тока в контуре, I_max – значение силы тока в контуре при резонансе);

–обобщенная расстройка контура (X и R– реактивное и активное сопротивления контура, соответственно);

- полоса пропускания контура;

- резонансная частота.

Выражение приведенной резонансной кривой регенерированного контура получается из аналогичного выражения для регенерированного контура при замене на. Так как, то выражение приведенной резонансной кривой имеет вид:

При слабых сигналах коэффициент регенерации определяется выражением (5) и тогда

.

При сильных сигналах и, следовательно,

.

Таким образом при сильных сигналах (при малых расстройках) резонансные кривые регенерированного и нерегенерированного контуров мало отличаются друг от друга. При слабых сигналах резонансная кривая регенерированного контура существенно зависит от параметра обратной связи и сужается по мере приближения к единице. На рисунке 6 изображены резонансные кривые для двух значений параметра обратной связи:и.

При слабых сигналах на границах полосы пропускания (по уровню 0,707) обобщенная расстройка равна

.

Следовательно, полоса пропускания регенерированного контура меньше полосы пропускания нерегенерированного:

или

Рисунок 6 – Резонансные кривые регенерированного контура

Регенеративное усиление может использоваться в схемах самого различного назначения, так как регенеративный усилитель представляет собой обычный избирательный усилитель с положительной обратной связью. В режиме усиления слабых сигналов регенеративный усилитель представляет собой линейную систему. Нелинейные свойства проявляются у него только в том случае, если сигналы выходят за пределы линейного участка характеристики. Наибольший интерес представляет использование регенеративного усиления в схемах радиоприема.