2.2.2 Интегрирующая цепь

Она представляет собой делитель напряжения на резисторе и конденсаторе, где выходное напряжение снимается с конденсатора(рисунок 7).

Рисунок 7 – Схема интегрирующей RC цепи

Проводя для интегрирующей цепи, такие же рассуждения, как и для дифференцирующей цепи, запишем

, где .

Тогда ,

т.е. комплексный коэффициент передачи интегрирующей цепи зависит от частоты.Определим модуль и аргумент коэффициента передачи

и .

Проведём анализ частотной зависимости.

• При стремлении частоты входного сигнала к нулю сопротивление конденсатора стремится к бесконечности, поэтому на месте конденсатора в схеме интегрирующей цепи получается разрыв (рисунок 8);

Рисунок 8 – Эквивалентная схема интегрирующей RC цепи при .

Рисунок 9 – Эквивалентная схема интегрирующей RC цепи при .

• На высоких частотах, при стремлении частоты входного сигнала к бесконечности, сопротивление конденсатора стремится к нулю и в эквивалентной схеме конденсатор можно заменить коротким замыканием (рисунок 9).

• При .

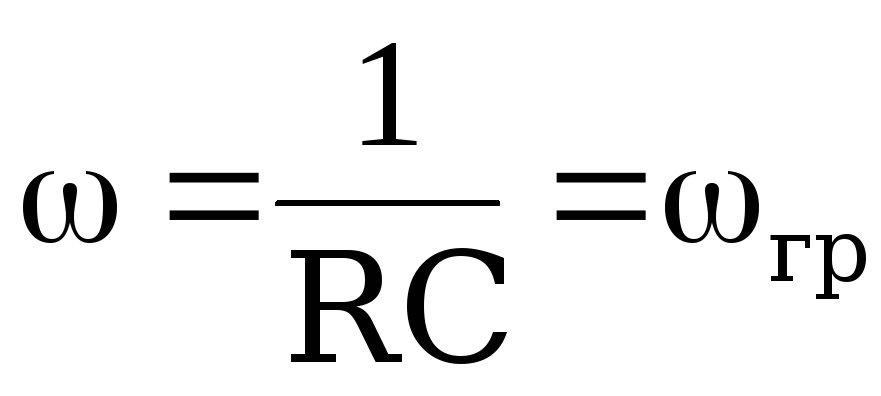
По результатам анализа зависимости интегрирующей цепи, можно построить амплитудно-частотную характеристику (рисунок 10).

Тангенс разности фаз между сигналом на выходе и на входе равен , откуда можно получить фазочастотную зависимость интегрирующей цепи:. Проанализируем эту зависимость:

• При стремлении к нулюстремится к нулю и.

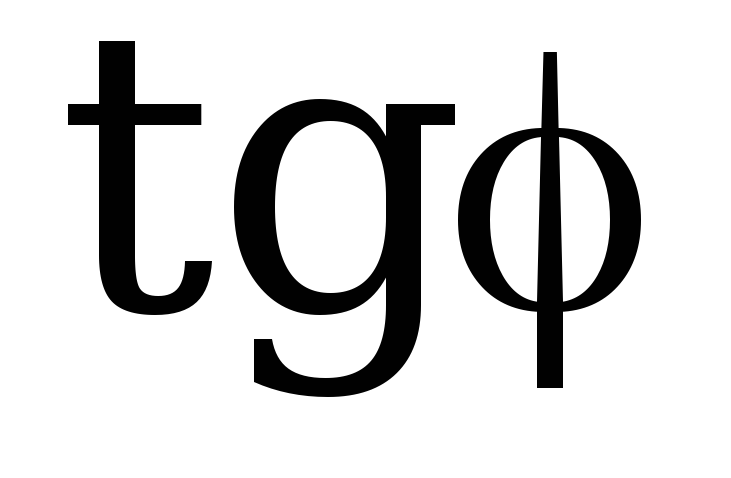• При стремлении к бесконечностистремится к минус бесконечности истремится к минус 90⁰.

• Пр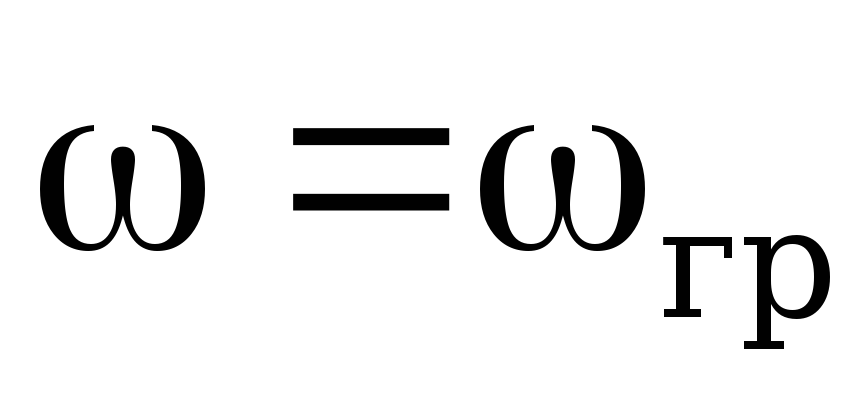и , и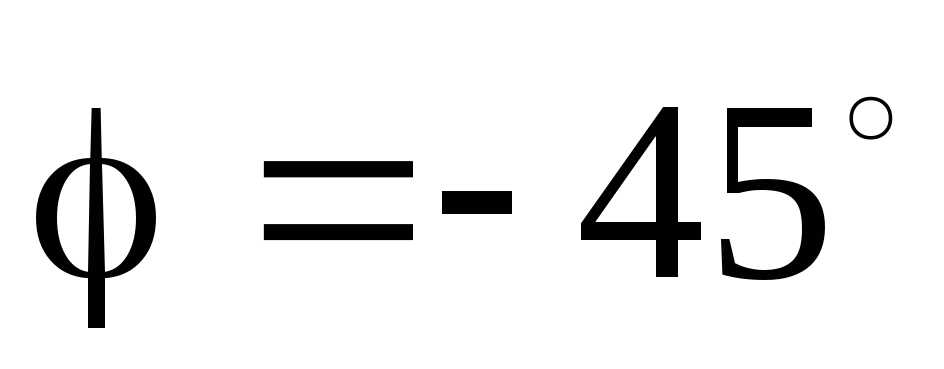

Фазочастотная характеристика данной интегрирующей цепи изображена на рисунок 11.

Рисунок – 10 Амплитудно-частотная характеристика интегрирующей цепи

Рисунок 11 – Фазочастотная характеристика интегрирующей цепи

2.2.3 Дифференцирующе–интегрирующая цепь

Цепь, которая состоит из соединенных последовательно дифференцирующей и интегрирующей цепей, называют дифференцирующее–интегрирующей цепью. Воспользуемся рассуждениями, изложенными выше, для дифференцирующей и интегрирующей цепей и получим комплексный коэффициент передачи дифференцирующее–интегрирующей цепи. Если напряжение на конденсаторе равно, то напряжение на резистореравно

Воспользовавшись уравнениями Кирхгофа, выразим через:

Проведем математические преобразования последнего выражения с учетом того, что и:.

Рисунок 12 – Схема последовательно соединённых дифференцирующей и интегрирующей цепей.

Определим выходное напряжение: или, обозначив граничную частоту, получим окончательно выражение для комплексного коэффициента дифференцирующее–интегрирующей цепи:.

Найдем модуль коэффициента передачи этой цепи:

.

Проанализируем полученную частотную зависимость:

 при

 при

 при .

При стремлении частоты к нулю или к бесконечности в схеме дифференцирующее–интегрирующей цепи конденсаторы можно заменить разрывом (рисунок 13) и коротким замыканием (рисунок 14), соответственно.

Рисунок 13 – Эквивалентная схема дифференцирующее–интегрирующей цепи при

Рисунок – 14 Эквивалентная схема дифференцирующее–интегрирующей цепи при

График амплитудно-частотной характеристики дифференцирующее–интегрирующей цепи имеет вид размытой резонансной кривой с максимумом на частоте ω₀, называемой квазирезонансной частотой (рисунок 15).

Выразим аргумент комплексного коэффициента дифференцирующее–интегрирующей цепи:

.

Проанализируем полученную частотную зависимость φ(ω):

• при ;

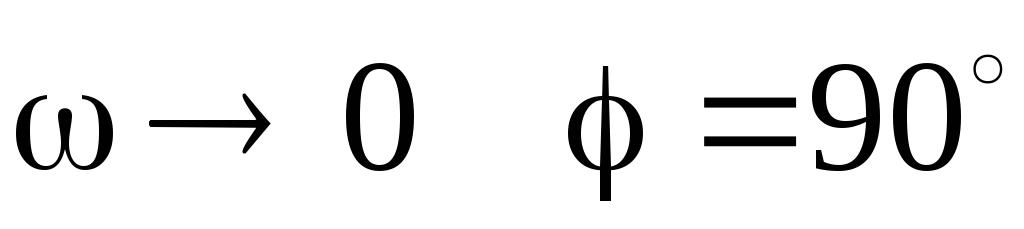• при ;

• при .

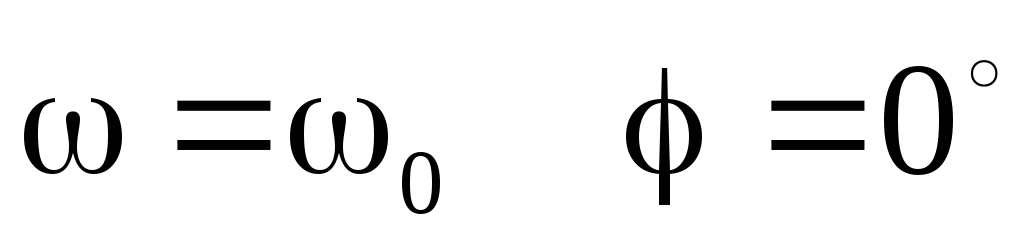Рисунок 15 – Амплитудно-частотная характеристика дифференцирующее–интегрирующей цепи

Рис. 16 – Фазочастотная характеристика дифференцирующее–интегрирующей цепи

Результаты анализа позволяют построить фазочастотную характеристику дифференцирующее–интегрирующей цепи (рисунок 16).