Эксперимент 2. Спектр гармонического сигнала с постоянным смещением.

Откройте файл с1_002 (рис. 1.2).

Для получения изображения спектральной характеристики гармонического сигнала, смещенного на постоянный уровень, необходимо на генераторе с помощью органа управления Off Set установить требуемое смещение, например равное 10 В, как показано на рис. 1.2а. Изображение такого сигнала на осциллографе приведено на рис. 1.26. После задания смещения, по команде Анализ > Запустить > Фурье..., получим на экране монитора изображение спектра сигнала в виде двух спектральных линий: постоянного смещения 10 В и гармоники с амплитудой 10 В и частотой 1 кГц, как показано на рис. 1.2в.

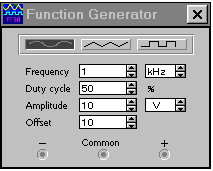а)

Рис. 1.2, а. Результаты анализа по Фурье гармонического сигнала с постоянной составляющей: установка генератора

б)

в)

Рис. 1.2б, в. Результаты анализа по Фурье гармонического сигнала с постоянной составляющей: изображение на осциллографе (б), изображение спектра (в)

Эксперимент 3. Спектр симметричных импульсов прямоугольной формы.

Откройте файл с1_003 (рис. 1.3).

Теперь выполним разложение в ряд Фурье симметричного периодического напряжения прямоугольной формы. Для этого на генераторе функций установим соответствующее выходное напряжение с амплитудой 10 В и частотой 1 кГц, как показано на рис. 1.3а. Изображение этого напряжения можно увидеть на осциллографе, как показано на рис. 1.3б.

После подачи команды Анализ > Запустить > Фурье... в окне Analysis Graphs появится изображение спектральной характеристики сигнала, которое приведено на рис. 1.3в. Из этого рисунка видно, что спектр прямоугольного импульса состоит из набора нечетных гармоник, амплитуды которых убывают обратно пропорционально номеру гармоники. Так, например, первая гармоника имеет частоту 1 кГц и амплитуду, равную 12,74 В. Третья гармоника с частотой 3 кГц имеет амплитуду 4,25 В (т. е. в три раза меньше амплитуды первой гармоники). Пятая гармоника с частотой 5 кГц имеет амплитуду 2,55 В, а седьмая гармоника с частотой 7 кГц — 1,82 В. Четные гармоники в спектре сигнала отсутствуют. В спектре сигнала нет также постоянной составляющей.

а) б)

в)

Рис. 1.3. Анализ по Фурье прямоугольного симметричного напряжения: установка генератора (а), изображение сигнала (б), спектральный состав (в)

Эксперимент 4. Спектр симметричных импульсов прямоугольной формы с постоянным смещением.

Откройте файл с1_004 (рис. 1.4).

Для получения однополярных симметричных прямоугольных импульсов нужно на генераторе функций установить постоянное напряжение смещения Off Set, например равное 10 В, как показано на рис. 1.4а. Изображение этого напряжения, которое появится на экране осциллографа, показано на рис. 1.4б.

а) б)

i

в)

Рис. 1.4. Анализ по Фурье смещенных прямоугольных импульсов: установка генератора (а), изображение сигнала (б) и его спектр (в)

После подачи команды Анализ > Запустить > Фурье... в окне Analysis Graphs можно увидеть частотный спектр этого сигнала, который отличается от рассмотренного выше спектра прямоугольных импульсов тем, что в нем присутствует постоянная составляющая, равная 10 В. Остальные спектральные составляющие не изменились.

Сравнение этих разложений в ряд Фурье с теоретическими значениями можно произвести, если воспользоваться данными теории. Так, для прямоугольных симметричных импульсов (эксперимент 3), спектральный состав которых определяется по формулам (1.1), имеем:

• амплитуда первой гармоники U_m1 = 4A_m/ = 40/ =12,74 В;

• амплитуда третьей гармоники U_m3 = 4A_m/(3) = 4,25 В;

• амплитуда пятой гармоники U_m5 = 4A_m/(5) = 2,55 В.

Аналогичный расчет можно выполнить для смещенных прямоугольных импульсов (эксперимент 4), которые содержат постоянную составляющую U_o = А_т /2= 10 В. Расчетные формулы для этого сигнала приведены в (1.2). Эти значения полностью совпадают со значениями спектральных составляющих, полученных путем моделирования, что подтверждает корректность выполненного решения.