Богатин а.С., Раевская с.И. Лабораторная работа №74

Изучение закона Ома для цепей переменного тока

Краткая теория

Рассмотрим электрические колебания, возникающие во внешней электрической цепи генератора переменного тока, электродвижущая сила которого изменяется периодически. Внешнюю цепь генератора составим из последовательно соединенных сосредоточенной емкости С (конденсаторы), сосредоточенной индуктивности L (катушки индуктивности, дроссели или обмотки трансформатора), резисторов R, как показано на рис. 1; в такой цепи будет протекать переменный ток, сила которого меняется по синусоидальному закону:

, (1)

где – амплитуда,– круговая частота.

Рис. 1

Переменный ток, протекающий в цепи, будем считать квазистационарным (как бы постоянным). Переменный ток можно считать квазистационарным, если за время , в течение которого изменения тока и напряжения передаются от одного конца цепи к другому, т.е. от точки 1 до точки 4 (рис. 1), сам ток и напряжение изменяются незначительно, а для этого необходимо, чтобы время было много меньше периода колебаний («). В этом случае к мгновенным значениям всех электрических величин можно применять законы постоянного тока и, в частности, законы Ома.

Наконец, будем считать, что колебания в цепи являются установившимися. Это значит, что с момента начала колебания прошло достаточно большое время, так что амплитуды тока и напряжения уже достигли постоянного значения, соответствующего величине внешней ЭДС.

Найдем, по какому закону изменяется напряжение на участках внешней цепи 1-2, 2-3, 3-4 и во всей цепи – 1-4, когда в ней течет ток, изменяющийся по синусоидальному закону (1).

1. На участке цепи 1-2 имеется резистор (активное сопротивление), сопротивление которого и течет переменный ток 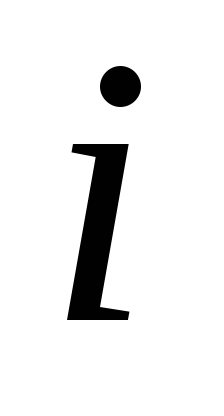, поэтому, согласно закону Ома, падение напряжения на нем:

. (2)

Таким образом, напряжение на концах участка 1-2 изменяется также по закону синуса. Напряжение и ток одновременно достигают максимальных значений и одновременно обращаются в нуль, поэтому разность фаз между колебаниями тока и напряжения равна нулю (рис. 2). Максимальное значение напряжения

(3)

есть амплитуда активной составляющей напряжения, а – круговая частота. Из формулы (3) следует, что амплитуда тока прямо пропорциональна амплитуде напряженияи обратно пропорциональна сопротивлению участка цепи. Формулу (3) иногда называют законом Ома для переменного тока, но нужно помнить, что эта формула относится только к амплитуде, но не к мгновенным значениям и .

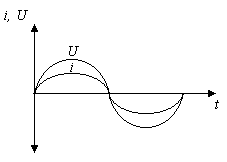
Рис. 2

Гармонически изменяющиеся величины напряжения можно изображать при помощи векторных диаграмм, которые строятся следующим образом: чертится горизонтальная линия, которая называется ось токов; относительно оси токов откладывается вектор, изображающий колебания напряжения. Длина этого вектора равна амплитуде напряжения, а угол между векторами напряжения и осью токов есть угол сдвига по фазе между током и напряжением. На рис. 3 изображена векторная диаграмма напряжения на резисторе.

Рис. 3

2. На участке цепи 2-3 имеется катушка индуктивности, к концам которой приложено переменное напряжение , которое вызывает в ней переменный электрический ток, изменяющийся по закону (1). При наличии переменного тока в катушке индуктивности возникает ЭДС самоиндукциии падение напряжения на ее активном сопротивлении(сопротивление провода), поэтому мы должны применить закон Ома для участка цепи с ЭДС:

.

Предположим, что сопротивление провода катушки очень мало и им можно пренебречь (), тогда приложенное к катушке напряжение в точности уравновешивает ЭДС самоиндукции и поэтому равно ЭДС самоиндукции с обратным знаком:, где. В этом случае

(4)

Сравнивая формулы (1) и (4), мы видим, что колебания напряжения на индуктивности опережают по фазе колебания тока на π/2 (рис. 4). Когда сила тока, возрастая, проходит через нуль, напряжение уже достигает максимума, после чего начинает уменьшаться; когда сила тока становится максимальной, напряжение проходит через нуль и т.д.

Из (4) видно, что амплитуда напряжения равна , следовательно, величинаиграет ту же роль, что и сопротивление участка. Поэтомуназываютиндуктивным сопротивлением (кажущимся сопротивлением индуктивности). Если индуктивность выражена в генри, авсек^-1, то будет выражено в омах.

Рис. 4

Рис. 5

Полученный результат можно представить векторной диаграммой. При построении векторной диаграммы примем за положительное направление вращения вектора напряжения относительно оси токов левое вращение (против часовой стрелки). Векторная диаграмма напряжения на индуктивности показана на рис. 5. Вектор напряжения, длина которого равна амплитуде напряжения , повернут относительно оси токов в положительном направлении на уголπ/2. У реальных катушек сопротивление проводов r ≠ 0, поэтому проложенное к катушке напряжение уравновешивают падение напряжения на активном и индуктивном сопротивлениях катушки. Закон Ома запишется в таком виде:

.

Таким образом, полное напряжение между концами катушки можно рассматривать как сумму двух гармонических колебаний: активной составляющей напряжения с амплитудой , совпадающей по фазе с током, и реактивной составляющей напряжения с амплитудой, отличающейся по фазе наπ/2.

Результирующее напряжение и угол, образованный результирующим вектором напряжения с осью токов, найдем, пользуясь векторной диаграммой напряжения.

Вектор активной составляющей напряжения, имеющий длину , откладываем на оси токов, вектор реактивной составляющей напряжения, имеющий длину, откладываем перпендикулярно к оси токов в положительном направлении, как показано на рис. 6. Тогда из рис. 6 следует, что длина результирующего вектора напряжения будет равна амплитуде действующего на катушке напряжения:

. (5)

Из (5) следует, что полное сопротивление катушки слагается из активнойи реактивнойсоставляющих, и эта формула выражает закон Ома для участка цепи, содержащей индуктивность.

Рис. 6