Богатин А.С., Раевская С.И.

Лабораторная работа № 61

Измерение сопротивления проводников

методом моста Уитстона

Краткая теория

Сопротивления проводников (в электротехнике такие детали именуются резисторами) обычно определяются по результатам измерения тока и напряжения (метод амперметра и вольтметра) и методом сравнения измеряемого сопротивления с образцовым (метод моста).

Первый метод основан на использовании закона Ома для участка цепи

,

где U_R – падение напряжения на R_x.

I_R – ток через R_x.

Вольтметр и амперметр могут быть включены в цепь по одной из следующих схем.

В

R_x

схеме рис. 1 вольтметр показывает напряжение на последовательно соединенных резисторе и амперметре. Поэтому напряжение на резисторе будет

,

где U, I, R_A – соответственно показания вольтметра, амперметра и сопротивление амперметра.

Следовательно,

R_x

В схеме рис. 2 амперметр измеряет суммарный ток, идущий через резистор и вольтметр. Поэтому

,

где R_V – сопротивление вольтметра.

Следовательно,

В схеме рис. 1 необходимо учитывать сопротивление амперметра, в схеме рис. 2 – сопротивление вольтметра.

Второй метод – метод моста постоянного тока (схема рис. 3) позволяет более точно производить измерения R_x, т.к. резисторы, используемые для измерений, можно выполнить с высокой степенью точности.

Мост постоянного тока (мост Уитстона) составлен из резисторов R_x, R, r₁, r₂, образующих «четырехугольник ABCD». В одну из диагональных ветвей – BD – включен гальванометр G, в другую – AC – источник эдс.

R_x – неизвестное сопротивление; R – известное, эталонное сопротивление. Ветвь AC, содержащая сопротивления r₁ и r₂ выполняется в виде реохорда, т.е. проволоки одинаковой толщины, вдоль которой может передвигаться контакт D. Этот контакт D делит сопротивление реохорда на части r₁ и r₂, которые для однородной проволоки одинаковой толщины пропорциональны соответствующим длинам l₁ и l₂ (т.к. , а  и S строго неизменны в любой точке реохорда). Перемещая контакт D, можно найти точку реохорда, потенциал которой равен потенциалу точки B. В этом случае ток через гальванометр не течет /мост сбалансирован/. В уравновешенном мосте ток в точках B и D не разветвляется. Используя второе правило Кирхгофа (в замкнутом контуре алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС) можно записать

(для контура ABD);

(для контура BCD).

Отсюда

Так как сопротивления участков реохорда пропорциональны длинам, то

(1)

(напомним, что l₁ = AD, l₂ = DC, l₁ + l₂ = L = AC – общая длина реохорда). Относительная погрешность результата равна

Величина определяется классом точности используемого магазина сопротивления. Найдем условие минимума погрешности. Общий знаменатель погрешности равен:

Очевидно, относительная погрешность будет минимальна, если величина общего знаменателя будет максимальна. Найдем условия максимума (первая производная должна быть равной нулю):

Т.е. , откуда .

Таким образом, погрешность минимальная, когда ползунок стоит на середине реохорда. В этом случае

и .

ИЗМЕРЕНИЯ

1. С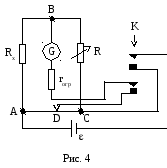хема измерений приведена на рис. 4. В процессе измерений сначала должна замыкаться цепь питания моста, а затем – цепь гальванометра. В схеме для этой цели служит двойной ключ K (при замыкании и размыкании цепи появляется ЭДС самоиндукции, которая вызывает экстратоки, опасные для гальванометра). В ветвь BD введено переменное сопротивление r_огр, ограничивающее ток через гальванометр (если мост не сбалансирован). По мере балансировки моста r_огр следует уменьшать до нуля. В качестве сопротивления R используется магазин сопротивлений.

Во избежание нагрева исследуемого резистора (сопротивление резистора меняется с температурой) мост под током должен находиться минимально возможное время.

Для получения максимальной точности измерений важно следить за чистотой контактов соединительных проводов и надежностью контакта движка с реохордом. Если R_x < 1 Ом, начнет сказываться сопротивление соединительных проводов (резисторы с малыми сопротивлениями исследуются другими мостовыми схемами).

2. Если движок реохорда установлен посередине (т.е. l₁ = l/2), исследуемое сопротивление R_x равно эталонному R. Отсюда методика пробного измерения: установив движок реохорда посередине, изменять сопротивление R до тех пор, пока ток через гальванометр не обратиться в нуль.

Внимание! Ключ K замыкать на короткое время!

3. Измерения с каждым исследуемым резистором провести несколько раз, изменяя l₁ и R. Результаты измерений и вычислений по формуле 1 заносить в таблицу вида:

Nизм	l1	L – l1	R	Rx	Rx
				Rxср = …	Rxср = …

В настоящей работе измерения проводятся:

а) с двумя резисторами R_x1 и R_x2;

R_x1 R_x2

б) с их последовательным соединением R_п: ;

R_x1

в) с их параллельным соединением R_ : .

R_x2

4. Вычислить погрешности измерений. Результат каждого измерения должен иметь вид: R_x  R_x.

5. Сравнить результаты измерений R_п с теоретическими . Сравнивать следует два интервала: (R_nосл  R_посл) и , где . Если указанные интервалы имеют общие значения – результаты можно считать совпадающими.

6. Сравнить результаты измерений R_ с теоретическими

. Учитывая, что ,

сравнение провести аналогично п. 5.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Каким преимуществом обладает метод определения сопротивления мостом Уитстона по сравнению с методом амперметра и вольтметра?

2. Почему на реохорде AC всегда можно найти такую точку D, потенциал которой равен потенциалу точки B?

3. Выведите условие равновесия моста.

4. Почему гальванометр, применяющийся в мостике Уитстона, имеет двустороннюю шкалу с нулем посередине?

5. Изменяется ли условие равновесия моста, если гальванометр и источник тока поменять местами?

5