5

Богатин а.С., Раевская с.И.

Лабораторная работа № 85

Изучение работы газоразрядного диода

Краткая теория

1. Газоразрядные лампы, используемые в настоящей работе, представляют собой заполненный одним или несколькими инертными газами стеклянный баллон, в который введены два электрода. Для газонаполненного диода зависимость тока от напряжения не подчиняется закону Ома и характеризуется особенностями, показанными на рис. 1.

П

I

ри малых напряжениях ток через лампу не течет (лампа «не горит»). При некотором значении приложенного напряжения U_заж энергия свободных электронов, имеющихся в газе, ста-

I_заж

новится достаточной для возбужде-

ния и ионизации атомов газа. Появ-

I_гаш

ление тока сопровождается возник-

новением свечения, цвет которого за-

висит от состава смеси газов в лампе.

Это свойство газоразрядных диодов

U

обусловило их широкое применение

U_гаш U_заж

в качестве самых разнообразных све-

товых индикаторов – цифровых, зна-

Рис. 1.

ковых, панельных и др. Скачком ус-

танавливаемая сила тока I_заж при

U=U_заж, при дальнейшем увеличении

напряжения возрастает по закону, близкому к линейному.

Уменьшение напряжения на горящей лампе (см. направление верхней стрелки на рис. 1) до U_заж не приводит к ее гашению ввиду того, что в баллоне еще остается некоторое количество положительных ионов, поддерживающих ток в лампе. Последняя перестает пропускать ток лишь при более низком напряжении («гашения») U_гаш. Сила тока при этом скачком падает от значения I_гаш до нуля.

Вольтамперная характеристика (ВАХ), изображенная на рис. 1, несколько идеализирована. У реальных ламп ВАХ не вполне линейна, причем ток при возрастании напряжения обычно не совпадает с током при убывании напряжения. Однако эти отличия носят второстепенный характер и на результаты лабораторной работы не влияют.

2. Подключение конденсатора к газоразрядному диоду позволяет получить колебательную систему – генератор релаксационных колебаний. В этом случае колебания являются совокупностью двух апериодических процессов – заряда и разряда конденсатора. (Подробно об этих процессах см. в лаб. работе № 91 «Изучение релаксационного процесса заряда – разряда конденсатора»). Рассмотрим механизм образования релаксационных колебаний в электрической цепи, изображенной на рис. 2 / Точка в кружке обозначает ионы газа в лампе/. При включении источника с напряжением Е посредством ключа К, начинается процесс

K

_

+

U

R

Е

I_c

C

I(U)

Рис. 2.

заряда конденсатора С через сопротивление резистора R; вследствие этого напряжение на обкладках конденсатора U_с возрастает по экспоненциальному закону до момента достижения U_c=U_заж. Поскольку сопротивление горящей лампы значительно меньше сопротивления резистора R, происходит быстрый разряд конденсатора до U_c=U_гаш, лампа

перестает проводить ток и конденсатор снова начинает заряжаться. Таким путем возникают колебания, представляющие собой чередование двух процессов – медленного заряда конденсатора через большое сопротивление и быстрого разряда его через гораздо меньшее сопротивление горящей лампы – см. рис. 3.

U_c

Т

Рассмотрим подробнее схему на рис. 2. При Е > U_заж по второму правилу

U_заж

Кирхгофа: I_c+I(U) = (E – U)/R, но

U_гаш

, поэтому получаем

t_разр

t_зар

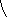
(1)

Если напряжение на конденсаторе

t

остается неизменным во времени, т.е.

Рис. 3.

постоянным, стационарным, то произ-

водная равна нулю и для стационарного тока I_ст находим (2)

Нетрудно видеть, что стационарный режим работы имеет место только при малых R. Случай, когда R=R_кр=(E–U_гаш)/I_гаш, является критическим, так как при дальнейшем увеличении R > R_кр, стационарный режим оказывается невозможным; в системе устанавливаются колебания (рис. 3) с амплитудой, равной размаху напряжения (U_заж – U_гаш).

Вычислим период Т релаксационных колебаний. Полное время колебания состоит из суммы времени заряда t_зар и времени разряда t_разр. Обычно сопротивление резистора R выбирают достаточно большим, существенно превосходящим сопротивление горящей лампы. В этом случае Тt_зар. Во время заряда конденсатора лампа не горит (I(U)=0) и уравнение (1) переходит в

(3)

Отсчитывая время с момента гашения лампы, т.е. U=U_гаш при t=0, будем иметь по формуле заряда конденсатора:

U=E–(E–U_гаш)exp(-t/RC) (4) В момент зажигания t = t_заж, U=U_заж, поэтому

U_заж=Е–(Е–U_гаш)ехр(-t_зар/RC) (5) Из (4) и (5) получаем

(6)

Изложенная теория является приближенной. Кроме отмеченных выше упрощающих расчеты предположений, полностью пренебрегнуты паразитные емкости и индуктивности в схеме. Не рассматриваются также процессы развития разряда и деионизации при гашении разряда. Теория справедлива лишь в тех случаях, когда в схеме установлена достаточно большая емкость и когда период колебаний существенно больше времен развития разряда и деионизации (практически при Т >> 10 мкс).