6

Богатин а.С., Раевская с.И. Лабораторная работа № 75 а

Изучение резонанса переменного тока

Литература для подготовки к выполнению лабораторной работы:

1. Калашников С.Г. Электричество. Учебное пособие. – 5-е издание, 1985 г., стр. 482 – 486.

2. Козлов В.И. Общий физический практикум. Электричество и магнетизм. Учебное пособие. Издательство МГУ, 1987 г., стр. 178– 189.

3. Физический практикум. Электричество и оптика. Под ред. Ивероновой В.И. - 2-е издание, 1968 г., стр. 274 – 277.

Порядок выполнения работы

1. Переключатель электрической цепи устанавливают в положение «J» - резонанс тока; переключатель вольтметра до окончания работы необходимо оставить в положении «U_L, рез. J».

2. Тумблером подключают цепь к источнику переменного тока с частотой 50 Гц и напряжением не более 50 В (лабораторный автотрансформатор, включаемый в сеть 220 В). Изменяя емкость конденсатора от 2 до 24 мкФ, через каждые 2 мкФ измеряют ток J_С , текущий через конденсатор, а также полный, суммарный ток J_∑ цепи.

3. По полученным данным строят общий график зависимостей J_С(С) и J_∑(С). По графику рассчитывают резонансную циклическую частоту ω₀ и линейную частоту ν₀ , определяют добротность контура Q = J_С /J_∑ .

4. Строят векторную диаграмму токов для исследованной цепи на резонансной частоте. Сопоставляют полученные значения добротности и частоты ν₀ для цепей резонанса напряжения и тока.

Контрольные вопросы

1. Начертите цепь, в которой возникает резонанс тока, и постройте векторную диаграмму токов как вдали от резонансной частоты, так и на частоте резонанса.

2. При каких условиях наступает резонанс переменного тока, какие величины характеризуют резонансные качества контура?

3. В чем сходство и различия явлений резонанса напряжений и резонанса токов? Приведите примеры их использования в радиотехнике.

ВНИМАНИЕ: Электрические цепи для наблюдения резонанса напряжений и резонанса токов собраны под дном панели с приборами и принадлежностями этой лабораторной работы, поэтому никаких внешних дополнительных соединений проводами ДЕЛАТЬ НЕ НАДО!

Выделение цепи для получения резонанса напряжений или резонанса токов осуществляется простым переключением тумблера в центре панели. После этого работа выполняется по порядку, изложенному в данном методическом описании (для резонанса токов см. выше).

Следите, чтобы максимальные значения напряжений и токов, достигаемых при резонансах, находились в пределах измерений соответ-ствующих приборов. В противном случае, т.е. при «зашкаливании» прибора, необходимо повысить сопротивление реостатом цепи или понизить подаваемое на схему напряжение.

Краткое теоретическое введение

Как известно [1], в цепи переменного тока, содержащей последовательно соединенные омическое сопротивление, индуктивность и емкость (рис. 1),

сила тока определяется по закону Ома:

.

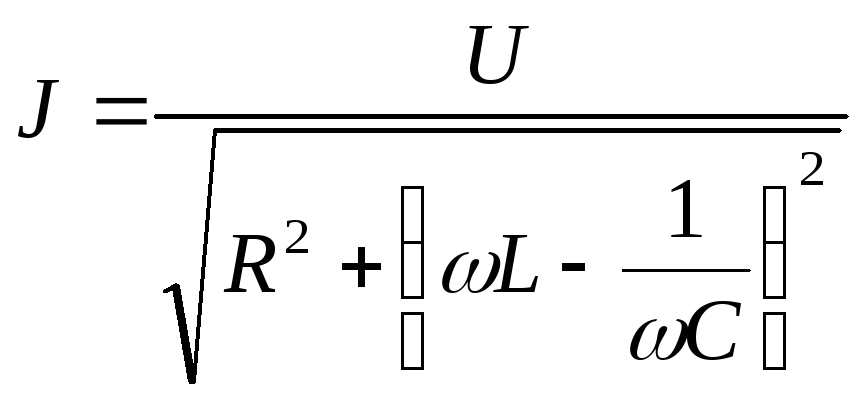Здесь представляется все омическое сопротивление цепи, включая и омическое сопротивление катушки.

Векторная диаграмма для случая, когда в цепи преобладает индуктивная нагрузка, т.е. падение напряжения на индуктивном сопро-тивлении превышает падение напряжения на емкостном сопротивлении, изображена на рис. 2. Сдвиг фаз между током и общим напряжением цепи определяется из выражения:

.

Тангенс сдвига фаз может получиться положительным или отрицательным в зависимости от того, преобладает ли в цепи индуктивное ωL > 1/ωС или емкостное 1/ωС > ωL сопротивление.

Рис.2

При некоторой частоте приложенного внешнего напряжения контура ω=ω₀, определяемой условием ω₀²=1/LC, реактивное сопротивление контура (ωL - 1/ωС) обращается в нуль. При этом амплитуда тока достигает максимального значения, а разность фаз между током и напряжением равна нулю, т.е. контур действует как чисто активное сопротивление.

Остановимся более подробно на этом практически очень важном случае вынужденных колебаний в последовательной цепи переменного тока, называемом явлением резонанса напряжений. Падение напряжения на индуктивности JωL и падение напряжения на емкости J/ωС в момент резонанса, будучи равны друг другу и противоположны по фазе, в то же время могут быть сколь угодно большими. Такое значительное повышение напряжения на емкости и индуктивности может привести к пробою диэлектрика конденсатора (или изоляции проводов). При резонансе внешнее приложенное напряжение, действуя в такт с собственными колебаниями системы, как бы раскачивает ее, причем амплитуда колебаний может достичь критических величин.

Частота, при которой наступает резонанс, в общем случае не равна частоте собственных колебаний контура

.

Однако в большинстве практических случаев , и поэтому с большим приближением этим различием можно пренебречь.

Исследование вынужденных колебаний в колебательном контуре сводится прежде всего к изучению зависимостей: 1) тока в цепи, 2) разности потенциалов на пластинах конденсатора, 3) напряжения на индуктивности – от соотношения между частотой вынуждающего воздействия и собственной частотой незатухающих колебаний в системе (ω₀² = 1/LC).

Соотношение между частотами ω и ω₀ может изменяться двумя способами: путем изменения ω₀ (т.е. параметров контура L или С) при ω=const или путем изменения частоты действующего в контуре напряжения при ω₀=const.

В настоящей работе применяется первый способ, а именно: соотношение между частотами ω и ω₀ изменяется путем изменения емкости. Зависимость тока в цепи от частоты имеет резонансный характер (рис. 3). Сила тока в момент резонанса при заданном напряжении определяется величиной активного сопротивления. Чем больше активное сопротивление цепи, тем слабее в ней проявляется резонанс.

Кривые U_L = f(ω) и U_С = f(ω) также имеют максимумы, однако достигаются они при частотах, отличных от ω₀ (рис. 4). Напряжение U_C = J/ωC достигает максимума до наступления максимума тока. Действительно, сила тока до резонанса возрастает быстрее, чем ω, потому U_C растет. Когда кривая тока подходит к резонансу, то нарастание становится все медленнее. В момент, когда нарастание силы тока и частоты сравняется, достигнет максимума U_C. Далее кривая тока будет нарастать медленнее, чем частота, и кривая U_C начнет убывать. Кривая U_L = ωLJ достигает максимума после максимума силы тока. Возрастание U_L происходит быстрее, чем U_C. Максимума U_C достигнет тогда, когда скорость убывания силы тока будет равна скорости возрастания частоты.

Для характеристики затухания колебательных контуров часто пользу-ются величиной, называемой добротностью контура Q. Она связана с логарифмическим декрементом затухания δ соотношением: Q = π/δ. Добротность контура есть умноженное на π число полных колебаний, по истечение которых амплитуда уменьшается в e раз. Добротность контура тем выше, чем меньше затухание в нем.

Добротность контура при резонансе есть отношение индуктивного (или емкостного) сопротивления к активному сопротивлению контура:

.

Отсюда следует, что при резонансе:

,

.

Целью настоящей работы является получение экспериментальным путем резонансных кривых для контуров с различными активными сопротивлениями и определение добротности контуров.

Описание приборов. При измерениях используются: исследуемые контуры, вольтметр с большим входным сопротивлением, который не шунтировал бы заметным образом конденсатор исследуемого контура, амперметр. Различные контуры создаются в ходе выполнения работы путем соединения одной катушки с разными конденсаторами и путем включения различных сопротивлений. Описание используемых в работе вольтметра и амперметра см. п.2.