5_КСЕ_Математика Древних и Средних веков 12_13
.pdf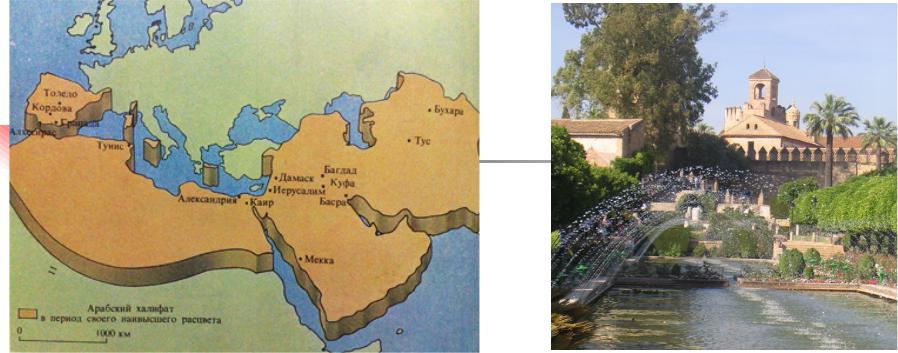
МАТЕМАТИКА В АРАБСКОМ ХАЛИФАТЕ
06.10.12 |
Е.Цупак |
41 |
http://elementy.ru/trefil/21136? context=20446
Liber abaci
Абак - самый древний счетный инструмент
Бухгалтерские
счёты
http://www.ksu.kst.kz/kib/museum.htm
06.10.12
Леонардо из Пизы (Фибоначчи) 1175–
1250
Арабские цифры в Европу пришли через Арабский Халифат. Итальянский математик Леонардо Фибоначчи в 1202 г. написал в
«Liber abaci» («Книге по арифметике»): «Девять индийских знаков суть следующие: 9, 8, 7, 6, 5, 4, 3, 2, 1.
С помощью этих знаков и знака 0, который называется по-арабски zephirum, можно написать какое угодно число».
http://shkolazhizni.ru/archive/0/n-38973/
Е.Цупак |
42 |
«Арабские» 
цифры
1 2 3 4 5 6 7 8 9 |
10 11 12 13 14….. |
|
|
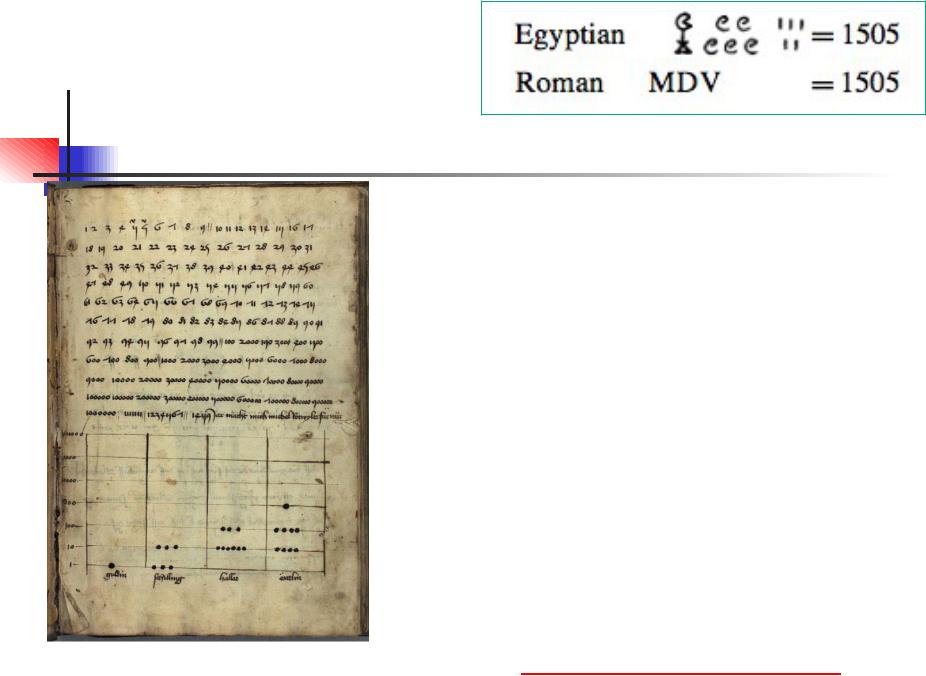
Ученые Европы до XVIIв. предпочитали не
связываться с арабскими цифрами, особенно с «0» (не могли понять идею
пустоты = 0). Банкиры и купцы стали пользоваться
ими почти везде в Европе лишь к середине к XV в.
германский06.10.12манускрипт 1459 года Е.Цупак |
43 |
http://www.supernovum.ru/forum/read.php?1,31116 |
|
http://chernykh.net/content/view/201/213/
Десятичная 
система
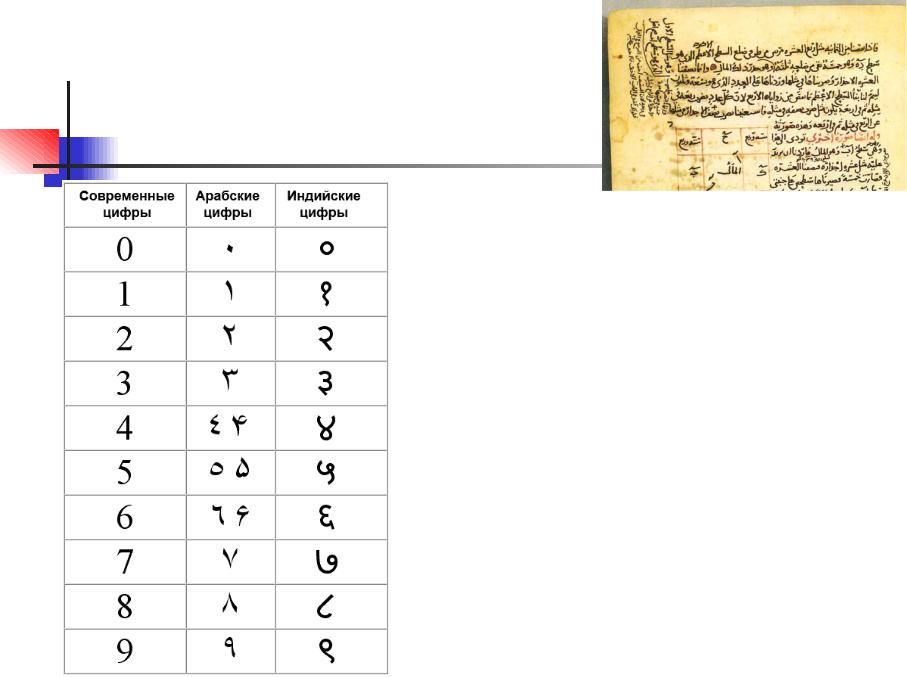
Трактат «Книга о сложении и вычитании на основе
индийского счисления» Мухамада аль-Хорезми:
nраспространение десятичной системы счисления и арабских
|
цифр, в т.ч. цифры «ноль»; |
|
|
|
nоперации |
, включая |
|
|
умножение и деление |
|
|
|
|
||
|
Изображение цифры «8» происходит |
||
|
из сокращённой записи латинского |
|
|
06.10.12 |
слова octo («восемь»). |
44 |
|
Е.Цупак |
|
||
Математик Аль-Хорезми
(IX в.)
в своей книге «Индийское искусство счета»:
«Если не остается ничего, то пишут маленький кружок, чтобы
место не оставалось пустым. Этот ок.780 – ок. 850 кружок должен занять место, потому что в противном случае у нас будет меньше разрядов, и второй, например, мы можем счесть за первый».
06.10.12 |
Е.Цупак |
45 |
Математика 
аль Хорезми
Трактат по алгебре «Книга о восполнении и противопоставлении» содержит уравнения первой и
второй степени. Классификация на шесть видов:
1. квадраты равны корням (пример 5x2 = 10x); 2. квадраты равны числу (пример 5x2 = 80); 3. корни равны числу (пример 4x = 20);
4. квадраты и корни равны числу (пример x2 + 10x = 39); 5. квадраты и числа равны корням (пример x2 + 21 = 10x);
6. корни и числа равны квадрату (пример 3x + 4 = x2).
Корнями уравнения Аль-Хорезми назвал значения переменной, при |
|
|
которых левая часть уравнения обращается в нуль. |
46 |
|
06.10.12 |
Е.Цупак |
|
|
Аль Хорезми 780-850г. |
|
Багдад |
Решение уравнений |
|
|
аль-Хорезми: x2 + 10x = 39 (IX |
век) имеет |
геометрическую формулировку: |
"Квадрат и |
корней равны 39". Геометрический |
метод его решения соответствует выделению полного
квадрата: |
= 39 |
|
|
|
|
x = 3 |
|
x + 5 = 8 |
(a + b)2 = a2 + 2ab + b2 |
||
|
|
|
|
Корнями уравнения Аль-Хорезми назвал значения переменной, при которых левая часть уравнения обращается в нуль.
06.10.12 |
h"p://school.iot.ru/predmety/matema<ka/05/main_1.htm |
47 |
Е.Цупак |
||
h"p://www.3elmwanoor.com/images/khawarizmi.jpg |
|
|
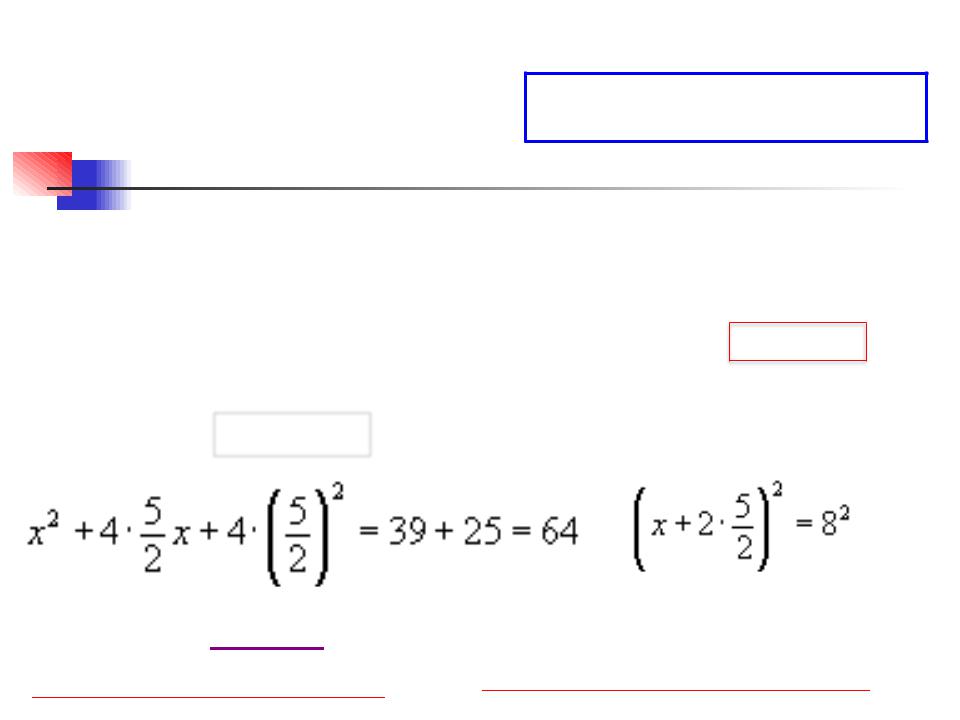
Математика 
аль Хорезми
x2 + 10x = 39
Уравнение (IX век) имеет в оригинале
: "Квадрат и десять корней равны 39". Геометрический метод его решения
полного квадрата: x2 + 10x = 39
(x + 5)2 = |
|
+ 52 |
(a + b)2 = a2 + 2ab + b2 |
|||
x2 + 10x |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 3 |
x + 5 = 8 |
||
|
|
|
06.10.12 |
h"p://school.iot.ru/predmety/matema<ka/05/main_1.htm |
48 |
Е.Цупак |
||
h"p://www.3elmwanoor.com/images/khawarizmi.jpg |
|
|
Математика аль Хорезми
Из « Книги об исчислении аль-джебры и алмукабалы»:
Пусть дано уравнение 6х -13 = 5х-8.
1) Прибавив к обеим частям по 13 и 8, совершим действие аль-джебр.
Получим 6х + 8 = 5х + 13.
2) Отнимая от обеих частей по 5х и по 8, совершим действие алмукабала и получим х = 5.
аль-джебр - алгебра ал-Хорезми ~ Algorithmus - алгоритм
06.10.12 |
Е.Цупак |
49 |
Математика 
аль Хорезми
«Книга о восполнении и противопоставлении» была дважды
переведена в XII веке на латынь и сыграла важную роль в развитии математики в Европе
В главе "о сделках" сформулировано Правило для нахождения неизвестного члена пропорции по трём
известным членам
1,2 кг яблок – 15 руб |
48 кг 15 руб |
х = = 600 руб |
|
48 кг яблок – х руб |
1,2 кг |
|
06.10.12 |
Е.Цупак |
50 |