
- •Конспекты лекций
- •Содержание
- •1.1. Функция спроса и предложения. Наклон кривой.
- •1.2. Наклон кривой спроса для нормальных товаров.
- •1.3. Наклон кривой предложения для нормальных товаров.
- •Литература основная
- •Динамические модели рынка одного товара
- •2.1. Паутинообразная модель рынка одного товара Дискретная модель.
- •2.2. Устойчивость равновесия. Сдвиг равновесия.
- •Контрольные вопросы
- •ПроизводствЕнная функция как модель процесса производства
- •3.1. Производственная функция и ее свойства.
- •3.2. Производство с одним переменным фактором.
- •3.3. Замещаемость производственных факторов.
- •3.4. Капиталоемкость технологии.
- •3.5. Эластичность замены одного фактора другим
- •3.6. Два крайних и общий случаи замещения факторов производства.
- •3.7. Изокоста (прямая равных издержек). Правило минимизации издержек фирмы.
- •3.8. Производство с двумя переменными факторами.
- •Контрольные вопросы
- •Литература основная
- •Научные работы профессора Германовой о.Е., используемые в преподавании микроэкономики
- •4.1. Издержки производства в краткосрочном периоде.
- •4.2. Издержки производства в долгосрочном периоде.
- •4.3. Доход фирмы: валовой, средний и предельный.
- •Контрольные вопросы
- •Литература основная
- •Научные работы профессора Германовой о.Е., используемые в преподавании микроэкономики
- •5. Деятельность фирмы на товарных рынках
- •5.1 Равновесие фирмы в условиях совершенной конкуренции.
- •5.2. Рынок чистой монополии. Основные признаки монополии.
- •5.3. Спрос, цена и предельный доход монополиста.
- •5.4. О кривой предложения монополиста.
- •5.5. Необходимое и достаточное условия максимизации
- •5.6. Показатель монопольной власти.
- •5.7. Ущерб, приносимый монополией.
- •5.8. Ценовая дискриминация
- •5.9. Регулирование деятельности монополии с помощью налогов.
- •Научные работы профессора Германовой о.Е., используемые в преподавании микроэкономики
Литература основная
Нуреев Р.М. Курс Микроэкономики. – М.: НОРМА-ИНФРА-М, 2008
Гальперин В.М., Игнатьев С.М., Моргунов В.И. Микроэкономика. Т.1. М., 2008
Гальперин В.М., Игнатьев С.М., Моргунов В.И. Микроэкономика. Т.2. М., 2008
Микроэкономика. Теория и российская практика / Под ред. Грязновой А.Г., Юданова А.Ю. М. КноРус, 2008
Микроэкономика: практический подход / Под ред. Грязновой А.Г., Юданова А.Ю. М. КноРус, 2009
Экономическая теория. /Под ред Н.Г. Кузнецова. М.: ИКЦ «МарТ; Ростов н/Д: Издательский центр «МарТ», 2008 Рекомендовано Министерством образования Российской Федерации в качестве учебника для вузов.
Динамические модели рынка одного товара
2.1. Паутинообразная модель рынка одного товара Дискретная модель.
Простейшие модели экономического равновесия разработаны в 30-50гг. 20-го века.
Рассмотрим рынок одного товара. Сделаем ряд допущений:
- у производителей не возникают трудности с покупкой ресурсов;
- объединим всех покупателей в одну группу и будем рассматривать их как одного покупателя;
- объединим всех продавцов в другую группу и будем рассматривать их как одного продавца;
- допустим, что весь произведенный товар реализуется сразу (единовременно).
Рассмотрим ситуацию на рынке, когда предложение товара постоянно отстает от спроса, в дискретном анализе на один интервал.
Интервалы времени одинаковы и последовательно принимают значения:

Если
 (time)
– текущий интервал времени, то
(time)
– текущий интервал времени, то
 – предшествующий, а
– предшествующий, а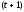 последующий интервал времени.
последующий интервал времени.
Такая
ситуация нередко наблюдается на рынке
нового товара. Функции спроса и предложения
на данный товар являются некоторыми
функциями от цены:
 и
и
Объем
товара
 произведен в предыдущем временном
интервале
произведен в предыдущем временном
интервале ,
а реализуется в текущем интервале
,
а реализуется в текущем интервале .
.
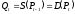
Производители
руководствуются ценой
 и производят продукцию в объеме
и производят продукцию в объеме .
Данное предложение товара реализуется
в следующем временном интервале по
новой цене спроса
.
Данное предложение товара реализуется
в следующем временном интервале по
новой цене спроса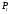 .
.
Общую схему действия модели можно представить следующим образом:
в
начальный интервал времени
 имеем
имеем ,
,
в
следующий интервал времени
 имеем
имеем и т.д.
и т.д.
Так как известны функции спроса и предложения, то можно определить равновесную цену. Для этого необходимо приравнять функции спроса и предложения:
 ,
,
где
 (equilibrium)
- индекс, означающий равновесное значение
величины объема и цены, соответственно
(
(equilibrium)
- индекс, означающий равновесное значение
величины объема и цены, соответственно
( ).
).
Если функции спроса и предложения линейны, то, приравнивая их, получим одну точку равновесия и единственное значением равновесной цены и равновесного объема.

Если функции спроса и предложения не линейны, то получим два или более значений равновесной цены и равновесного объема. В таком случае необходимо провести дополнительное исследование и определить, в какую точку равновесия приходит система под влиянием спроса и предложения и факторов их определяющих.
Проиллюстрируем
графически паутинообразную модель.
Первоначально находимся в точке
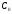 .
В этой точке производители руководствуются
ценой
.
В этой точке производители руководствуются
ценой и производят продукцию в объеме
и производят продукцию в объеме в период времени
в период времени .
.
Реализуется
товар в точке
 в периоде
в периоде по цене спроса
по цене спроса .
В периоде
.
В периоде производители увеличивают предложение
товара до
производители увеличивают предложение
товара до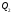 ,
так как выросла цена товара, и находятся
в точке на кривой предложения с
координатами
,
так как выросла цена товара, и находятся
в точке на кривой предложения с
координатами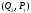 .
.
Продается
товар в точке
 .
Поскольку предложение товара возросло,
то, чтобы продать весь товар, приходится
снизить цену с
.
Поскольку предложение товара возросло,
то, чтобы продать весь товар, приходится
снизить цену с до
до .
.
В
следующий период времени
 производители руководствуются ценой
производители руководствуются ценой ,
производят объем продукции
,
производят объем продукции в точке на кривой предложения с
координатами
в точке на кривой предложения с
координатами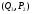 .
Реализуется эта продукция по цене
.
Реализуется эта продукция по цене в точке
в точке и т.д. Рынок приходит в состояние
равновесия в точкеС.
и т.д. Рынок приходит в состояние
равновесия в точкеС.
Аналитическая интерпретация модели состоит в следующем:
Для простоты будем считать, что спрос и предложение являются линейными функциями:
 ;
;
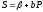 ,
,
где
 – конкретные параметры каждого товара.
– конкретные параметры каждого товара.
Находим
равновесные объем и цену, приравняв
функцию спроса и предложения:




 .
.
Подставим
равновесное значение цены в функции
спроса и предложения и определим
равновесный объем:
 .
Так как в точке равновесия объем спроса
равен объему предложения, то справедливо
выражение:
.
Так как в точке равновесия объем спроса
равен объему предложения, то справедливо
выражение:
 .
(1.1)
.
(1.1)
Запишем
условие равновесия для любого времени
 :
:
 (1.2)
(1.2)
Выражение (1.2) справедливо для любой точки. Знак равенства в выражении (1.2) означает, что весь произведенный продукт реализован.
Вычтем из уравнения (1.2) уравнение (1.1):
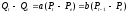 .
.
Перейдем к следующим обозначениям:
 характеризует
отклонение объема выпуска в любой период
времени от равновесного объема выпуска;
характеризует
отклонение объема выпуска в любой период
времени от равновесного объема выпуска;
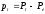 представляет
отклонение цены спроса в любой момент
времени от равновесного значения;
представляет
отклонение цены спроса в любой момент
времени от равновесного значения;
 -
отклонение цены предложения в любой
момент времени от равновесного значения.
-
отклонение цены предложения в любой
момент времени от равновесного значения.
Тогда действие модели можно представить разностными уравнениями:
 (1.3).
(1.3).
Выражение (1.3) аналогично выражению (1.2), но описывает отклонения цены и выпуска в некоторый период времени от их равновесных значений.
Из
уравнения (1.3) можно выразить значение
цены в любой период времени
 следующим
образом:
следующим
образом: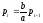 .
Обозначим
.
Обозначим ,
тогда
,
тогда .
Величина
.
Величина ,
так как наклон кривой спроса для
нормальных товаров отрицателен
,
так как наклон кривой спроса для
нормальных товаров отрицателен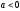 ,
а наклон кривой предложения – положителен
,
а наклон кривой предложения – положителен .
.
Так
как
 ,
то
,
то ,
где
,
где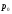 - известная величина – цена в начальный
период времени
- известная величина – цена в начальный
период времени ,
а
,
а можно определить из уравнения (1.3),
поскольку известны функции спроса и
предложения.
можно определить из уравнения (1.3),
поскольку известны функции спроса и
предложения.
Во все периоды времени имеем:
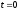

 ;
;


 ;
;


 ;
;


 ,
,
т.е.
для любого периода времени
 имеем
имеем .
Отсюда
.
Отсюда


 .
.
Отклонение
цены в любой период времени от ее
равновесного значения
 принимает то положительные, то
отрицательные значения. Так как начальное
отклонение
принимает то положительные, то
отрицательные значения. Так как начальное
отклонение ,
то
,
то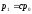 - положительная величина.
- положительная величина.
Число
 - величина отрицательная, так как
- величина отрицательная, так как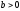 - наклон кривой предложения,
- наклон кривой предложения, - наклон кривой спроса. Обозначим
- наклон кривой спроса. Обозначим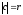 .
Тогда
.
Тогда
 ;
;
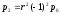 ;
;
 ;
;
….;
 ,
т.е. знак отклонения
,
т.е. знак отклонения
 будет чередоваться: минус, плюс, минус
и т.д. Следовательно,
будет чередоваться: минус, плюс, минус
и т.д. Следовательно, будет то меньше, то больше равновесной
цены.
будет то меньше, то больше равновесной
цены.
У данной модели есть развитие. Под влиянием неценовых факторов спроса и предложения кривые спроса и предложения перемещаются, и с помощью модели можно рассматривать, как рынок приходит в состояние равновесия до того периода пока не возникает новое возмущение.
Например, в спокойное течение дел на рынке вмешивается резкий рост предложения, если продавцы выбрасывают запасы товара. В новой ситуации в анализе рынка товара следует соединить рассмотренную модель с моделью включения запаса.
Непрерывная модель.
В
модели время течет непрерывно,
 ,
и все параметры являются функциями
времени:
,
и все параметры являются функциями
времени: ,
, ,
,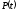 .
Поскольку изменение цены происходит
на стороне спроса, то спрос зависит от
цены
.
Поскольку изменение цены происходит
на стороне спроса, то спрос зависит от
цены и ее изменения
и ее изменения ,
а предложение зависит только от цены.
В каждый момент времени спрос поглощает
предложение, т.е.
,
а предложение зависит только от цены.
В каждый момент времени спрос поглощает
предложение, т.е. .
.
Используем
линейные функции спроса и предложения
в следующем виде:
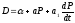 ;
; .
.
Определим равновесные значения цены и объема, приравняв функции спроса и предложения:
 .
(1.4)
.
(1.4)
Так
как в точке равновесия цена задана
рынком, то
 Значения
Значения и
и в любой момент времени удовлетворяют
равенству:
в любой момент времени удовлетворяют
равенству:
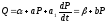 .
(1.5)
.
(1.5)
Вычитаем из выражения (1.5) выражение (1.4) и получим:
 .
.
Как
и в дискретной модели вводим обозначение:
 .
Тогда
.
Тогда .
В новых обозначениях выражение (1.5)
принимает вид:
.
В новых обозначениях выражение (1.5)
принимает вид:
 (1.6)
(1.6)
Уравнения
(2) и (3) представляют собой дифференциальные
уравнения первого порядка. Обозначаем
 ,
тогда
,
тогда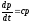

 .
.
 -
дифференциальное уравнение относительно
-
дифференциальное уравнение относительно
 .
.
Используя
правило логарифмического дифференцирования,
получим:
 .
Решение имеет вид:
.
Решение имеет вид: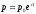 ,
, .
Следовательно,
.
Следовательно,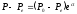

 .
Зная цену, и подставив ее в функцию
предложения, всегда можно найти объем
продукции, который надо произвести.
.
Зная цену, и подставив ее в функцию
предложения, всегда можно найти объем
продукции, который надо произвести.
