Министерство науки и высшего образования Российской Федерации

федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский университет «Московский институт электронной техники»

Институт микроприборов и систем управления имени Л.Н. Преснухина

Отчет по лабораторной работе № 4

«Расчет дискретных (цифровых) фильтров. Проектирование фильтров с конечными импульсными характеристиками»

по курсу

«Цифровая Обработка Сигналов»

Выполнил Студент РТ-33	Л азба Ф.Б. / _______________
Преподаватель	Мелёшин Ю.М. / _______________

Москва 2021

Введение

Цель работы:

1. Закрепить теоретические знания по проектированию нерекурсивных цифровых фильтров, полученные на лекциях;

2. Научиться пользоваться аппаратом MATLAB для синтеза нерекурсивных цифровых фильтров по заданной частотной характеристикой, в т.ч. согласованных с типовыми радиотехническими сигналами, и в определении характеристик синтезированных фильтров.

3. Научиться пользоваться различными функциями взвешивания (оконными функциями, весовыми функциями) при синтезе фильтров.

4. Получить первичные навыки в применении функций MATLAB для синтеза нерекурсивных цифровых фильтров.

Используемое оборудование или ПО: MatLab 2010/2014/2018/2020.

Задание на выполнение:

1. C помощью функций: рассчитайте нерекурсивный полосно-пропускающий фильтр с линейной ФЧХ, предназначенный для квазиоптимальной фильтрации прямоугольного радиоимпульса длительностью 6 мкс, на несущей (промежуточной) частоте (1,167) МГц. Исследуйте зависимость полосы пропускания и уровня пульсаций в полосе задерживания от порядка фильтра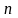 , принимая значения из ряда 8, 16, 32, 64 и т.д. (до достижения требуемой полосы пропускания). Результаты исследования оформите в виде таблицы.

Определите реакцию фильтра на входное воздействие в виде прямоугольного радиоимпульса при согласованной полосе пропускания (совпадает с полосой сигнала по первым нулям его спектра), при полосе пропускания больше на 30% чем полоса сигнала и меньше на 30% чем полоса сигнала. Полученные графики привести в отчете. Объясните получившиеся результаты.

2. C помощью функции рассчитайте, пожалуйста, режекторный фильтр, предназначенный для подавления промежуточной частоты 6 МГц на выходе детектора. Ширина полосы сигнала: 76 кГц.

Для неискаженного приема информации необходимо, чтобы фильтр обеспечивал подавление промежуточной частоты не менее -40 дБ в полосе сигнала КГц.

По значениям коэффициентов нерекурсивного фильтра рассчитайте и постройте графики импульсной характеристики, амплитудночастотной и фазочастотной характеристик. Определите уровень запирания в заданной полосе запирания и пропускания на частоте .

Задание 1

f=1.167 Mhz

6 мкс

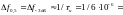0.167 МГц

1. Выберем частоту дискретизации =16 МГц. Аналогично предыдущему примеру определим вектор частот, вектор значений АЧХ

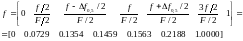
Вектор значений АЧХ .

2. Рассчитываем вектор коэффициентов по исходным данным для 8 с помощью программы

%РАСЧЕТ ПОЛОСОВОГО ФИЛЬТРА КВАЗИОПТИМАЛЬНОГО К РАДИОИМПУЛЬСУ

a=[1]; %вектор коэфф рекурсивной части

n=8; %порядок фильтра

f= [0 0.0729 0.1354 0.1459 0.1563 0.2188 1.0000 ]; %вектор частот частотной х-ки

m=[0.1 0.1 0.707 1 0.707 0.1 0.1]%вектор значений частотной х-ки (частотных отсчетов)

b=fir2(n,f,m); %вектор коэфф нерекурсивной части

%определяется для полосового фильтра порядка n

%и векторов частот и значений АЧХ

Impz(b,a); %построение импульсной характеристики

figure

freqz(b,a) %построение частотной характеристики

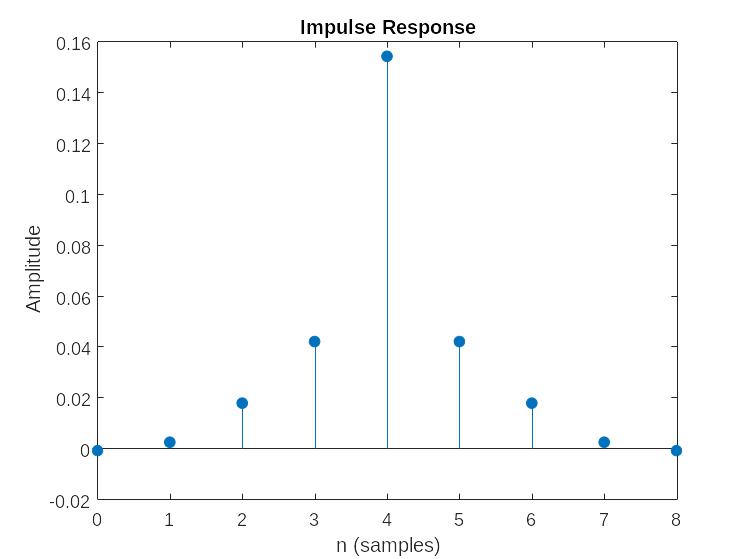
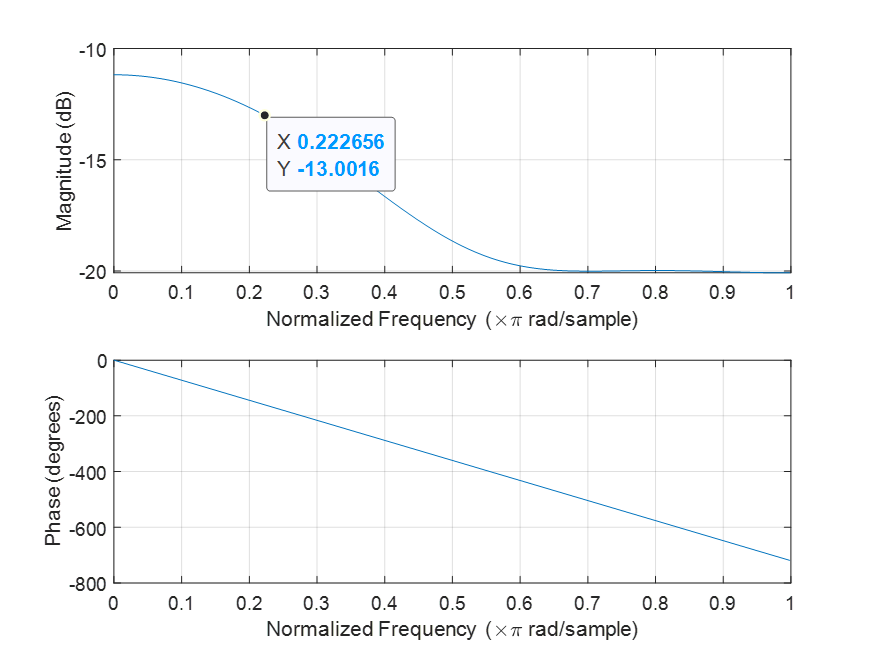
в) В результате расчетов получаем частотную характеристику, по которой полоса пропускания фильтра явно не соответствует заданной (0.223*f_Н вместо 0,167). Кроме того, такой вид АЧХ скорее характерен для ФНЧ, чем для полосового фильтра.

г) С целью достижения заданного значения полосы пропускания будем увеличивать порядок фильтра. Повторим вычисления для 16, 32, 64, 128, 256, определяя при этом ширину полосы пропускания

Порядок фильтра n	Параметры частотной характеристики
	Граничная частота полосы пропускания fГП1, МГц	Граничная частота полосы пропускания fГП2, МГц	Центральная частота полосы пропускания fПП, МГц	Ширина полосы пропускания ΔfПП, МГц	Неравномерность АЧХ в полосе пропускания ΔAпп, Дб	Граничная частота полосы задерживания по уровню 0,01 fГЗ, МГц	Ширина переходной области ΔfПЕР, МГц	Крутизна АЧХ в переходной области ΔAПЗ/ΔfПЕР, дБ/МГц	Уровень боковых лепестков в области задерживания AБГЗ, дБ
n=8	0	2.232	1.116	2.232	3	5.6	3.368	-2.078	отс
n=16	0	1.968	0.984	1.968	3	3.184	1.216	-5.756	отс
n=32	0.71	1.576	1.144	0.864	3	2	0.424	-16.51	отс
n=64	0.872	1.432	1.152	0.560	3	1.68	0.248	-28.22	отс
n=128	0.936	1.368	1.152	0.432	3	1.624	0.256	-27.34	отс
n=256	1	1.328	1.164	0.328	3	1.592	0.264	-26.51	отс
n=512	1.04	1.28	1.16	0.240	3	1.576	0.296	-23.64	отс

Необходимая ПП была получена для 32 порядка. Приведем ИХ, АЧХ, ФЧХ

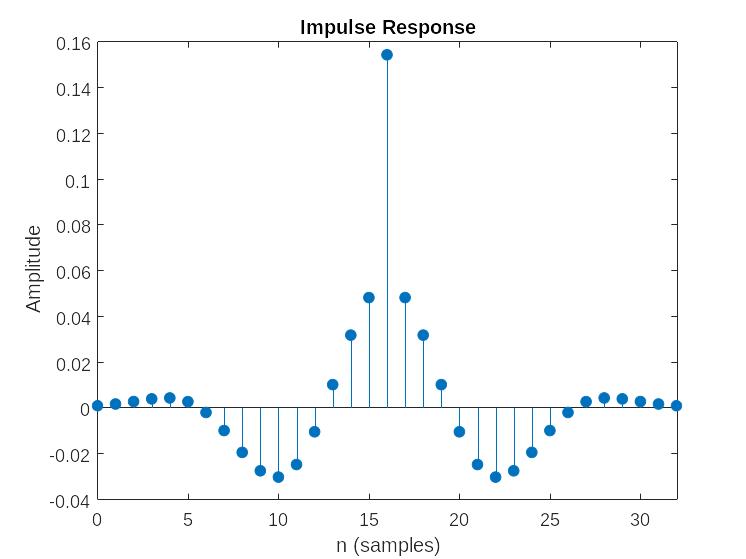
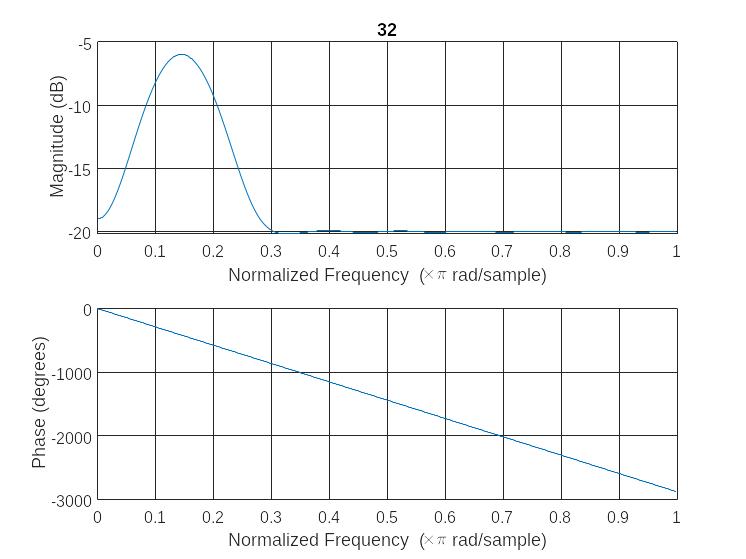
е) Для трех из приведенных выше случаев ( 16, МГц, 32, МГц и 64, МГц) с помощью известной нам функции дискретной фильтрации вычислим реакцию на исходный сигнал - прямоугольный радиоимпульс. Используем программу

%РАСЧЕТ ПОЛОСОВОГО ФИЛЬТРА КВАЗИОПТИМАЛЬНОГО К РАДИОИМПУЛЬСУ И ПРОХОЖДЕНИЕ РАДИОИМПУЛЬСА ЧЕРЕЗ ФИЛЬТР

a=[1]; %вектор коэфф рекурсивной части

n=16; %порядок фильтра

f= [0 0.0729 0.1354 0.1459 0.1563 0.2188 1.0000 ]; %вектор частот частотной х-ки

m=[0.1 0.1 0.707 1 0.707 0.1 0.1]%вектор значений частотной х-ки (частотных отсчетов)

b=fir2(n,f,m); %вектор коэфф нерекурсивной части

%определяется для полосового фильтра порядка n

%и векторов частот и значений АЧХ