2. Примеры решения типовых задач расчета нерекурсивных фильтров (ких-фильтров)

1. C помощью MATLAB (функции 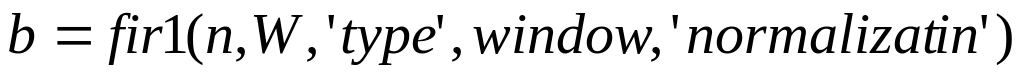рассчитайте нерекурсивный полосно-пропускающий фильтр с линейной ФЧХ, предназначенный для квазиоптимальной фильтрации прямоугольного радиоимпульса длительностью 1 мкс, на несущей (промежуточной) частоте 8 МГц, частоту дискретизации примите равной 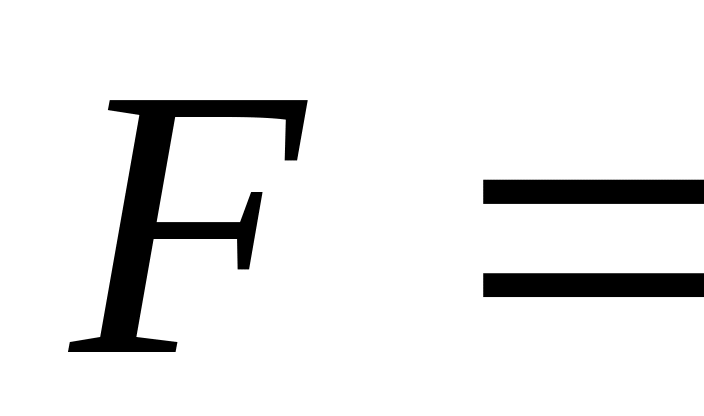64 МГц. Исследуйте зависимость полосы пропускания от порядка фильтра.

Решение.

1. Для квазиоптимальной фильтрации одиночного прямоугольного радиоимпульса применяется полосовой фильтр, настроенный на частоту несущей 8 МГц, с полосой пропускания 1 МГц. Для задания требуемой частотной характеристики определим значения частот в долях частоты Найквиста (половины частоты дискретизации ). Вектор граничных частот полосы пропускания полосового фильтра определится .

2. Вектор коэффициентов нерекурсивного фильтра для 8 и графики ИХ, а также АЧХ и ФЧХ могут быть рассчитаны с помощью следующей программы

%РАСЧЕТ НЕРЕКУРСИВНОГО ПОЛОСОВОГО ФИЛЬТРА ПО ПОРЯДКУ И ВЕКТОРУ ЧАСТОТ СРЕЗА КВАЗИОПТИМАЛЬНОГО К РАДИОИМПУЛЬСУ

a=[1]; %вектор коэффициентов рекурсивной части

W=[0.2334 0.2656]; %частоты среза

n=8; %порядок фильтра

b=fir1(n,W) %вычисление вектора коэффициентов нерекурсивной части

%определяется для нерекурсивного полосового фильтра порядка n

%с граничными частотами полосы пропускания W=[w1 w2]

%в долях частоты Найквиста = F/2

Impz(b,a); %построение импульсной характеристики

figure

freqz(b,a); %построение частотной характеристики

3. В результате расчетов получаем вектор коэффициентов нерекурсивной части 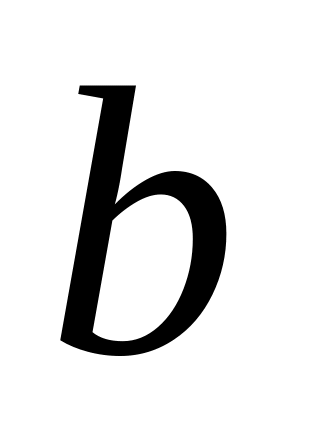=[-0.0355 -0.0673 0.0008 0.2736 0.4467 0.2736 0.0008 -0.0673 -0.0355] и импульсную характеристику, состоящую из =8 + 1 = 9 отсчетов (рис.1).

Рис.1. Импульсная характеристика полосового НРЦФ для n=8.

4. В результате расчетов получаем частотную характеристику (рис.2), по которой полоса пропускания фильтра составляет 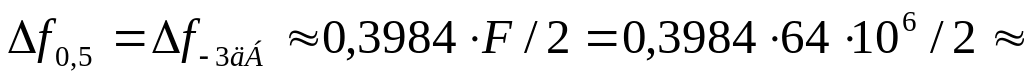12,75 МГц. Кроме того, такой вид АЧХ скорее характерен для ФНЧ, чем для полосового фильтра.

Рис.2. Комплексная частотная характеристика полосового НРЦФ для n=8: а – амплитудная частотная характеристика, б – фазовая частотная характеристика.

5. С целью достижения заданного значения полосы пропускания будем увеличивать порядок фильтра. Повторим вычисления для 16, 32, 64, 128, 256, определяя при этом ширину полосы пропускания

Получаем для 16; МГц

Получаем для 32; МГц

Получаем для 64; МГц

Получаем для 128; МГц. Для этого случая приводим графики ИХ и АЧХ и ФЧХ (рис.3)..

Рис.3. Характеристики НРЦФ для 128 МГц: а – импульсная характеристика, б - амплитудная частотная характеристика, в – фазовая частотная характеристика

Таблица 1 – Зависимость параметров АЧХ нерекурсивного полосового фильтра, синтезированного с помощью функции , от порядка фильтра

Порядок фильтра n	Параметры частотной характеристики
	Граничная частота полосы пропускания fГП1, МГц	Граничная частота полосы пропускания fГП2, МГц	Центральная частота полосы пропускания fПП, МГц	Ширина полосы пропускания ΔfПП, МГц	Неравномерность АЧХ в полосе пропускания ΔAпп, Дб	Граничная частота полосы задерживания по уровню 0,01 fГЗ, МГц	Ширина переходной области ΔfПЕР, МГц	Крутизна АЧХ в переходной области ΔAПЗ/ΔfПЕР, дБ/МГц	Уровень боковых лепестков в области задерживания AБГЗ, дБ
n=8	0	12,74	7,5	12,74	3	20,31	7,57	2,24	отс
n=16	5,51	8,00	10,49	4,98	3	14,12	3,63	4,68	-35
n=32	6,75	9,31	8,00	2,56	3	11,06	1,75	9,71	-38,2
n=64	7,36	8,64	8,00	1,28	3	9,5	0,86	19,77	-40,4
n=128	7,68	8,32	8,00	0,64	3	8,73	0,41	41,46	-42,2

Получаем для 16 МГц

Получаем для 32 МГц

Получаем для 64 МГц

Получаем для 128 МГц. Для этого случая приводим графики.

6. Для трех из приведенных выше случаев ( 16, МГц, 64, МГц и 128, МГц) с помощью известной нам функции дискретной фильтрации вычислим реакцию на исходный сигнал - прямоугольный радиоимпульс. Используем программу

%РАСЧЕТ ПОЛОСОВОГО ФИЛЬТРА КВАЗИОПТИМАЛЬНОГО К РАДИОИМПУЛЬСУ И ПРОХОЖДЕНИЕ РАДИОИМПУЛЬСА ЧЕРЕЗ ФИЛЬТР

a=[1]; %вектор коэфф рекурсивной части

W=[0.2334 0.2656]; %частоты среза

n=128; %порядок фильтра

b=fir1(n,W) %вектор коэфф нерекурсивной части

%определяется для полосового фильтра порядка n

%и граничных частот полосы пропускания W=[w1 w2]

%в долях частоты Найквиста = F/2

Fs=64e6; %частота дискретизации 64 МГц

f=8e6; %несущая частота 8 МГц

tau=1.0e-6; %длительность радиоимпульса 1 мкс

t=-tau:1/Fs:2*tau; %вектор дискретных значений времени nT

A=rectpuls(t-tau/2, tau);%расчет отсчетов прямоугольного импульса A(nT)

u=A.*sin(2*pi*f*t); %расчет отсчетов ралиоимпульса u(nT)

y=filter(b, a, u); %вычисление реакции фильтра

subplot(2,1,1) %определение места №1 графика в матрице 1х2

%figure

plot(u) %построение входного сигнала

title('INPUT SIGNAL u(n)') %заголовок