Xlabel('Нормированная частота') %подпись по оси X

ylabel('Амплитуда') %подпись по оси y

grid on % добавление сетки

subplot(2,1,2) %определение места №2 графика в матрице 1х2

stem(n-1,phi) % построение ФЧХ

title(' ФАЗОВЫЙ СПЕКТР') %заголовок

Xlabel('Нормированная частота') %подпись по оси X

ylabel('Фаза') %подпись по оси y

grid on % добавление сетки

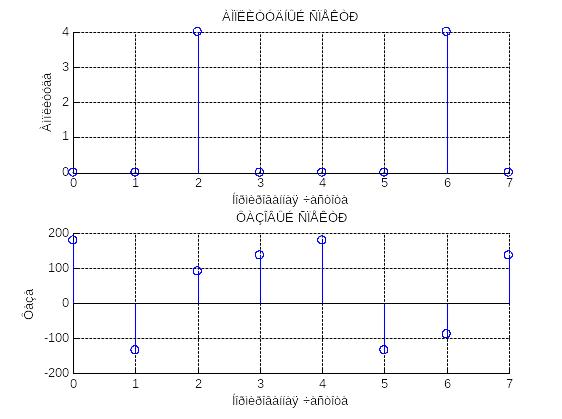
Рис.6. Результат выполнения восьмиточечного БПФ гармонического сигнала

2. С помощью MATLAB выполните, пожалуйста, обратное ДПФ (восстановить временную зависимость ) по известному вектору восьмиточечного БПФ s = [0 0 0 0 0 0 8j 0].

Решение.

1. Для восстановления временной зависимости по известному спектру необходимо выполнить обратное дискретное преобразование Фурье, в основе которого также лежит прямое ДПФ.

В соответствии с условиями задачи выполним прямое ДПФ (БПФ) над комплексно сопряженным спектром .

%ИССЛЕДОВАНИЕ ОБРАТНОГО БПФ ДЛЯ K=8

clear

%СПЕКТР СИГНАЛА ДЛЯ ОБПФ

K=8

k=1:K %формирование последовательности k

s=[0 0 0 0 0 0 -8j 0]%вектор отсчетов спектра s(k)

%s=conj(s) %вычисление комплексносопряженного спектра

% ВЫЧИСЛЕНИЕ АМПЛИТУДНОГО И ФАЗОВОГО СПЕКТРОВ

scompl=s; % результат выполнения восьмиточечного БПФ

a=abs(scompl); % амплитудный спектр сигнала

phi=(180/pi)*angle(scompl); % фазовый спектр сигнала

% ПОСТРОЕНИЕ ГРАФИКОВ АМПЛИТУДНОГО И ФАЗОВОГО СПЕКТРОВ

figure

subplot(2,1,1) %определение места №1 графика в матрице 1х2

stem(k-1,a); % построение амплитудного спектра

title('SPECTR N=8') %заголовок

xlabel('k, (kmax=N-1), [frequency samples]') %подпись по оси x

ylabel('Magnitude, [V]') %подпись по оси y

grid on % добавление сетки

subplot(2,1,2) %определение места №2 графика в матрице 1х2

stem(k-1,phi) % построение ФЧХ

xlabel('k, (kmax=N-1), [frequency samples]') %подпись по оси x

ylabel('Phase, [degrees]') %подпись по оси y

grid on % добавление сетки

%ДВУХТОЧЕЧНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ (ЧЕТЫРЕ)

un21=[s(1)+s(5) s(1)-s(5)] %вектор первого (из четырех) двухточечного БПФ

un22=[s(3)+s(7) s(3)-s(7)] %вектор второго (из четырех) двухточечного БПФ

un23=[s(2)+s(6) s(2)-s(6)] %вектор третьего (из четырех) двухточечного БПФ

un24=[s(4)+s(8) s(4)-s(8)] %вектор четвертого (из четырех) двухточечного БПФ

%ЧЕТЫРЕХТОЧЕЧНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ (ДВА)

un41=[un21(1)+un22(1) un21(2)-j*un22(2) un21(1)-un22(1) un21(2)+j*un22(2)] %вектор первого (из двух) четырехточечного БПФ

un42=[un23(1)+un24(1) un23(2)-j*un23(2) un23(1)-un24(1) un23(2)+j*un23(2)] %вектор первого (из двух) четырехточечного БПФ

%ВОСЬМИТОЧЕЧНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ

un8=[un41(1)+un42(1) un41(2)+(exp(-j*pi/4))*un42(2) un41(3)+(exp(-j*pi/2))*un42(3) un41(4)+(exp(-j*3*pi/4))*un42(4) un41(1)-un42(1) un41(2)-(exp(-j*pi/4))*un42(2) un41(3)-(exp(-j*2*pi/4))*un42(3) un41(4)-(exp(-j*3*pi/4))*un42(4)] %вектор восьмиточечного БПФ

un8=(un8)/K

figure

% ПОСТРОЕНИЕ ГРАФИКА СИГНАЛА (ДЕЙСТВИТЕЛЬНОЙ И МНИМОЙ ЧАСТИ)

n=k

subplot(2,1,1)

axis tight; % масштаб такой, чтобы вошел весь

% диапазон значений по обеим осям

plot(n-1,real(un8)); % график сигнала

title('SIGNAL u(n)'); % заголовок графика

xlabel('n, (n max=N-1), [samples]'); % надписи по горизонтальной оси

ylabel('real(u(n)), [V]'); % надписи по вертикальной оси

grid on

subplot(2,1,2)

axis tight; % масштаб такой, чтобы вошел весь

% диапазон значений по обеим осям

plot(n-1,imag(un8)); % график сигнала

xlabel('n, (n max=N-1), [samples]'); % надписи по горизонтальной оси

ylabel('image(u(n)), [V]'); % надписи по вертикальной оси

grid on

В результате вычисления получаем un = [-j 1 j -1 -j 1 j -1] (рис.7).

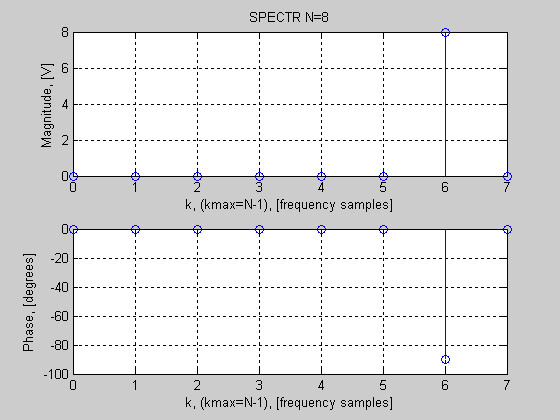
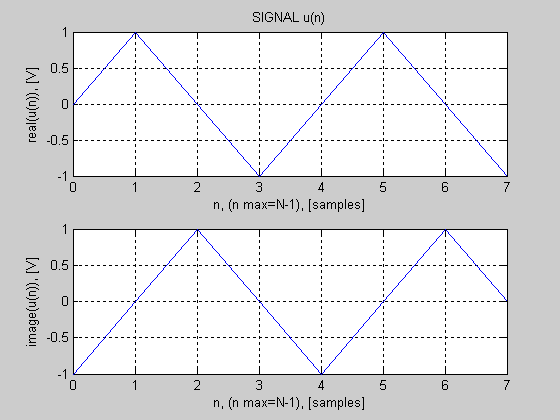
Рис.7. Результат вычисления обратного ДПФ спектра s = [0 0 4j 0 0 0 -4j 0] – временная последовательность .

3. C использованием возможностей, предоставляемых MATLAB (программа fft) выполните прямое ДПФ с размером выборки 64 для косинусоидального сигнала для случая, когда на выборке укладывается целое количество периодов сигнала 16 и для нецелого количества периодов 16,3 и 18.

Для уменьшения эффекта растекания спектра, имеющего место в случае, когда на выборке укладывается нецелое число периодов сигнала, примените к весовую функцию – окно Хэмминга.

По результатам вычислений заполните таблицу 2.

Таблица 2 – Спектр гармонического сигнала (основная область) для различных значений периода

Функция
№ част. отсчета	0	1	2	3	4	5	6	7	8	9	10
Величина
Функция
№ част. отсчета	0	1	2	3	4	5	6	7	8	9	10
Величина
Функция
№ част. отсчета	0	1	2	3	4	5	6	7	8	9	10
Величина
Функция , взвешивание по Хэммингу
№ част. отсчета	0	1	2	3	4	5	6	7	8	9	10
Величина

Решение.

1. Выполним прямое ДПФ для косинусоидального сигнала с периодом =16 (рис. 8,а) – на периоде БПФ содержится целое количество периодов сигнала .

% ПРЯМОЕ БПФ

T=16; %период гармонического сигнала u(n)

n=1:1:64; %вектор номеров отсчетов n

un=cos(2*pi*n/T) %вектор отсчетов un

scompl=fft(un);% комплексный спектр сигнала

s=abs(scompl); % амплитудный спектр сигнала

phi=180/pi*angle(scompl); % фазовый спектр сигнала

subplot(2,1,2) %определение места №1 графика в матрице 1х2

stem(n-1, s); % построение амплитудного спектра

title('АМПЛИТУДНЫЙ СПЕКТР') %заголовок