
Цифровая обработка сигналов ЦОС / Матлаб / Лаба 6 / C6_195_Sklizkov_Dmitry_RT_31
.pdf
Лабораторная работа 6
Склизков Дмитрий РТ-31
Задание 3.
3) Для когерентно-импульсной РЛС (см. рис.3) рассчитайте параметры гребенчатого фильтра на базе процессора ДПФ (минимально необходимый размер выборки N и период (интервал) дискретизации T ) для выработки оценок радиальной составляющей скорости целей. Значение несущей частоты РЛС f =
1,7 ГГц, максимальное значение радиальной скорости цели VRMAX =5400 км/ч, потенциальное значение ошибки не должно превышать 10 м/с. Для упрощения задачи время прихода сигнала будем считать известным, шумовой и динамической ошибкой в оценках точности можно пренебречь.
ОпределитереакциюДПФ-процессоранасигнал,отраженныйотцели,имеющей радиальную составляющую скорости V =1000; 1500; 10; 0 м/с.
Эффект Доплера:
Эффе́кт До́плера — изменение частоты и, соответственно, длины волны излучения, воспринимаемой наблюдателем (приёмником), вследствие движения источника излучения относительно наблюдателя (приёмника)

ДПФ-процессор – прибор, который получает на вход сигнал от цели и анализирует его с помощью дискретного преобразования Фурье
Частота волны, отраженной от приближающегося объекта (v отрицательная) увеличивается. От уходящего объекта (v положителная) – уменьшается.
Гетеродин - это частота сигнала , которая создается путем объединения или смешивания двух других частот
clc clear all close all
format short g
V_rmax = 5400 / 3600 * 1000 %перевод в м/с V_rmin = 10
f_nes = 1.7*10^9 c = 3 * 10^8
f_dmax = 2 * V_rmax / c * f_nes %макс. знач. доплеровской частоты f_dmin = 2 * V_rmin / c * f_nes %разрешение по допплеровской частоте
F_s = f_dmax * 2 t=0:1/F_s:1/f_dmin; n=t*F_s;
vr=1500; %действующая рад. скорость fd=2*vr*f_nes/c un=exp(j*2*pi*fd*t); scompl=fft(un);
s=abs(scompl);
phi=180/pi*angle(scompl);
subplot(2,1,1)
stem(n,un)
title(' ВХОДНОЙ СИГНАЛ') xlabel('Отсчеты времени') ylabel('Отсчеты сигнала') grid on
subplot(2,1,2) stem(n, s);
title('АМПЛИТУДНЫЙ СПЕКТР') xlabel('Нормированная частота') ylabel('Амплитуда')
grid on hold on
V_rmax = 1500 %максимальная радиальная скорость
V_rmin = 10 %минимальная радиальная скорость f_nes = 1.7e+09 %несущая частота
c = 300000000 %скорость света
f_dmax = 17000 %максимальная частота по Доплеру f_dmin = 113.33 %минимальная частота по Доплеру
F_s = 34000 %период следования (период дискретизации), исходя из условия однозначного измерения максимального Доплера
fd = 1700 %текущий Доплер
Отсчеты сигнала
ВХОДНОЙ СИГНАЛ
1





















0.5
0
-0.5
-1
0 |
50 |
100 |
150 |
200 |
250 |
300 |
Отсчеты времени
АМПЛИТУДНЫЙ СПЕКТР
200
150
Амплитуда |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
50 |
100 |
150 |
200 |
250 |
300 |
Нормированная частота
Отсчеты сигнала
ВХОДНОЙ СИГНАЛ
1


















0.5
0
-0.5 |
|
0 |
50 |
300
200
Амплитуда |
100 |
|
100 |
150 |
200 |
Отсчеты времени
АМПЛИТУДНЫЙ СПЕКТР
250 |
300 |
0 |
|
|
|
|
|
|
0 |
50 |
100 |
150 |
200 |
250 |
300 |
Нормированная частота

Отсчеты сигнала
ВХОДНОЙ СИГНАЛ
1
0.5
0
-0.5
-1 |
|
|
|
|
|
|
0 |
50 |
100 |
150 |
200 |
250 |
300 |
Отсчеты времени
АМПЛИТУДНЫЙ СПЕКТР
300
Амплитуда
200
100
0 |
|
|
|
|
|
|
0 |
50 |
100 |
150 |
200 |
250 |
300 |
Нормированная частота
ВХОДНОЙ СИГНАЛ
1 |
Отсчеты сигнала
0.5
0
0 |
50 |
100 |
150 |
200 |
250 |
300 |
Отсчеты времени
Амплитуда
АМПЛИТУДНЫЙ СПЕКТР
300 
200
100
0 |
|
|
|
|
|
|
0 |
50 |
100 |
150 |
200 |
250 |
300 |
Нормированная частота
Задание 4
N и период (интервал) дискретизации T ) для выработки оценок
радиальной составляющей скорости целей при неизвестной дальности (неизвестном времени прихода сигнала). Исходные данные для расчета из примера 1, скважность последовательности зондирующих импульсов в РЛС КНИ Q =5.
Задачу решить в общем виде – время прихода сигнала неизвестно. Шумовой и динамической ошибкой в оценках точности можно пренебречь.
Определите реакцию ДПФ-процессора на сигнал, отраженный от цели, имеющей значения радиальной составляющей скорости те же, что и в предыдущей задаче.
fdmax = |
17000 |
|
fdmin = |
113.33 |
|
vr = |
|
1500 |
Fsl = |
|
8500 |
T = |
1.1765e-05 |
|
N = |
750 |
|
clc close all clear
f=1.7e9; %несущая частота
vrmax=5400 / 3600 * 1000; %максимальная радиальная скорость vrmin=10; %минимальная радиальная скорость
%(точность (чувствительность) измерения радиальной скорости) fdmax=2*vrmax*f/3e8 %максимальный допплер fdmin=2*vrmin*f/3e8 %минимальный допплер
%(предел чувствительности допплеровского измерителя) vr=1500 %текущая радиальная скорость
fd=2*vr*f/3e8; %текущий допплер
Fsl=fdmax/2 %период следования (ЗДЕСЬ НЕ РАВЕН периоду дискретизации), определяется исходя из условия однозначного измерения максимального допплера
taui=1/(Fsl*5)
T=taui/2 %интервал дискретизации N=1/(fdmin*T)%размер выборки процессора ДПФ
t=0:T:1/fdmin;%вектор времени n=t/T; %временные отсчеты
d=(0:(Fsl/fdmin))' *1/Fsl;%вектор описывающий положение импульсов сигнала на временной оси в пределах n от 0 до N
un1=pulstran(t,d,'tripuls',2*taui); %последовательность треугольных после оптимальной фильтрации в приемнике) видеоимпульсов
un=un1.*exp(j*2*pi*fd*t); %отсчеты сигнала, полученные в результате
%выделения с помощью ФД модуляции последовательности видеоимпульсов Доплером цели scompl=fft(un);% комплексный спектр сигнала
s=abs(scompl); % амплитудный спектр сигнала phi=180/pi*angle(scompl);
subplot(2,1,1) %определение места 1 графика stem(n,un) %построение графика сигнала title(' ВХОДНОЙ СИГНАЛ')
xlabel('Отсчеты времени') %подпись по оси x ylabel('Отсчеты сигнала') %подпись по оси y grid on % добавление сетки

subplot(2,1,2) %определение места 2 графика stem(n, s); % построение амплитудного спектра title('АМПЛИТУДНЫЙ СПЕКТР') ylabel('Амплитуда')
xlabel('Нормированная частота') grid on
hold on
Отсчеты сигнала
ВХОДНОЙ СИГНАЛ
1














0.5
0 |
|
0 |
100 |
150
100 
Амплитуда |
50 |
|
200 |
300 |
400 |
500 |
600 |
Отсчеты времени
АМПЛИТУДНЫЙ СПЕКТР
700 |
800 |
0 |
|
|
|
|
|
|
|
|
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
Нормированная частота
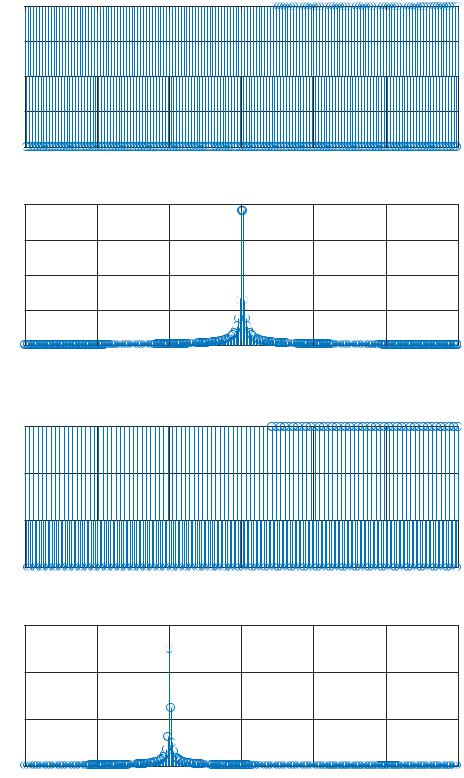
Максимальный уровень сигнала наблюдаем на выходе n=150, что соответствует радиальной скорости 150*10=1500 м/с

Отсчеты сигнала
ВХОДНОЙ СИГНАЛ
1
0.5
0 



































-0.5 |
|
0 |
100 |
150
100
Амплитуда |
50 |
|
200 |
300 |
400 |
500 |
Отсчеты времени
АМПЛИТУДНЫЙ СПЕКТР
600 |
700 |
800 |
0 |
|
|
0 |
100 |
200 |
V=1000 m/c
300 |
400 |
500 |
600 |
700 |
800 |
Нормированная частота
ВХОДНОЙ СИГНАЛ
1 |
0.5 |
Отсчетысигнала |
0 |
-0.5 |
-1
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
Отсчеты времени
Амплитуда
АМПЛИТУДНЫЙ СПЕКТР
150
100
50
0
-50
-200 |
0 |
200 |
400 |
600 |
800 |
Нормированная частота
V = 10 m/c

ВХОДНОЙ СИГНАЛ
1














Отсчеты сигнала
0.5 





























0
0
150 
100
Амплитуда |
50 |
|
100 |
200 |
300 |
400 |
500 |
600 |
Отсчеты времени
АМПЛИТУДНЫЙ СПЕКТР
700 |
800 |
0 |
|
|
|
|
|
|
|
|
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
Нормированная частота
V= 0 m/c
Задание 5
Рассчитайте параметры фильтра на базе процессора БПФ, согласованного с одиночным ЛЧМ-импульсом, имеющим следующие параметры – длительность импульса N =512 T , где T - период дискретизации, f1 =0,03F - минимальное значениенесущейчастоты, f2 =0,06 F - максимальноезначениенесущейчастоты. Сравните полученные результаты фильтрации с аналогичным по длительности одиночнымрадиоимпульсомпо крутизненарастания выходного напряжения вблизи максимума.

ЛМЧ-сигнал
clc clear close all
%БЫСТРАЯ СВЕРТКА. СОГЛАСОВАННЫЙ ФИЛЬТР НА БАЗЕ ПРОЦЕССОРА БПФ %CИГНАЛ ЛЧМ
N=511 %размер выборки ДПФ n=0:1:N; %вектор отсчетов времени T=1 %период дискретизации t=0:T:N*T; %вектор времени
f0=0.03 %минимальное значение частоты ЛЧМ-сигнала f1=0.06 %максимальное значение частоты ЛЧМ-сигнала
t1=N*T %длительность ЛЧМ-сигнала (время изменения частоты от %минимального до максимального значения uin=chirp(t,f0,t1,f1,'linear'); %вычисление вектора отсчетов
%входного ЛЧМ-сигнала
h=uin(N-n+1); %формирование вектора импульсной характеристики %фильтра, согласованного с сигналом uin
uou=fftfilt(h,uin); %вычисление быстрой свертки subplot(3,1,2) %определение места No2 графика в матрице 1х2 stem(h); % построение импульсной характеристики title('ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА') %заголовок xlabel('Отсчеты времени') %подпись по оси x ylabel('Амплитуда') %подпись по оси y
grid on % добавление сетки
subplot(3,1,1) %определение места No1 графика в матрице 1х3 stem(uin); % построение графика входного сигнала title('ВХОДНОЙ СИГНАЛ') %заголовок
xlabel('Нормированная частота') %подпись по оси x ylabel('Амплитуда') %подпись по оси y
grid on % добавление сетки
subplot(3,1,3) %определение места No3 графика в матрице 1х3
