
Тестирование.ГМУ
..docТестирование
Специальность 080504.65 – Государственное и муниципальное управление
|
№ |
Наименование дидактической единицы ГОС |
|
|
|
1 |
Алгебра |
|
|
|
2 |
Математический анализ |
|
|
|
3 |
Теория вероятностей и матстат. |
|
|
|
|
|
|
|
-
Определитель матрицы
 равен ответ 1. Решение = sin22x
+ cos22x
=1.
равен ответ 1. Решение = sin22x
+ cos22x
=1.
2. Даны матрицы А =
 и В =
и В =
 , то С = 2АТ – 3В =
, то С = 2АТ – 3В =
 .
.
Решение: С = 2АТ – 3В = 2 - 3
- 3 =
=
 .
.
3. Ранг матриц A = (a1,
a2, a3)
a1 =
![]()
![]() a2 =
a2 =
![]() a3 =
a3 =
![]() равен: ответ 3.
равен: ответ 3.
Решение: A = (a1,
a2, a3)
=
 и имеет 3 ненулевых строки.
и имеет 3 ненулевых строки.
4. Дана матрица А =
![]()
![]() . Тогда матрица А-1 может иметь
вид: А-1=
. Тогда матрица А-1 может иметь
вид: А-1=
 .
.
Решение: достаточно проверить выполнение
равенства АА-1 =
![]()
 =
=
![]() .
.
_________________________________________________________________________________
5. Система несовместна
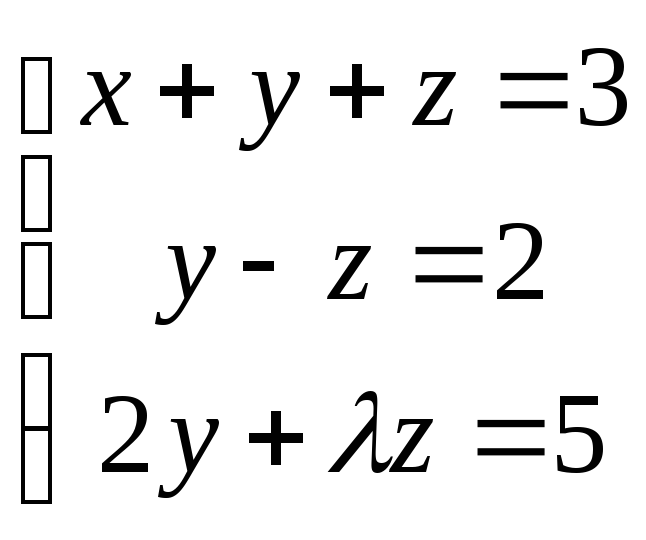 если
если
![]() равно. Ответ: при
равно. Ответ: при
![]() = -2.
= -2.
Решение: система несовместна, если ранг матрицы не равен рангу расширенной матрицы. В примере ранг расширенной матрицы равен 3. Ранг матрицы будет меньше 3, если
 =
=
![]() + 2 = 0.
+ 2 = 0.
6. Среди представленных линейных множеств линейное пространство не образует:
Ответ: множество всех векторов пространства R2 образующих острый угол с положительным направлением оси координат.
7. Область определения функции
![]() имеет вид: ответ
имеет вид: ответ
![]() .
.
Решение: Область определения находится
как решение системы ![]() .
.
_________________________________________________________________________________8.
Предел
![]() равен: Ответ 0,5.
равен: Ответ 0,5.
Решение:
![]() =
=
![]() =
=
![]() = =
= =![]() = 0,5.
= 0,5.
9. Значение производной по переменной
x функции
![]() в точке (0,-1) равно:
в точке (0,-1) равно:
Решение: для функции, заданной неявно
F(x,y) = 0,
искомая производная находится по
формуле yx’
= - Fx’(x,y)/Fy’(x,y).
Поэтому имеем yx’
= -
![]() .
yx’(0,-1)
= 1/3.
.
yx’(0,-1)
= 1/3.
10. Сумма наибольшего и наименьшего
значений функции
![]() на отрезке
на отрезке
![]() равна: Ответ: 3,5.
равна: Ответ: 3,5.
Решение: наибольшее и наименьшее значение
функции ищем в точках «-2», «0» - концах
сегмента и точках, принадлежащих сегменту
![]() ,
в которых производная функции равна
нулю. Имеем
,
в которых производная функции равна
нулю. Имеем
![]() 3(x+1)(x-2)
= 0 при x = - 1.
3(x+1)(x-2)
= 0 при x = - 1.
f(-2)=-1, f(-1)= 4,5, f(0) = 1. Искомая сумма равна 3,5.
11. Уравнение наклонной асимптоты графика
функции
![]() имеет вид y = kx
-1. Тогда k равно … Ответ:
-2.
имеет вид y = kx
-1. Тогда k равно … Ответ:
-2.
Решение: коэффициент равен пределу
![]()
12.Приближенное значение выражения
![]() вычисленное приближенно с помощью
первого дифференциала приближенно
равно … Ответ 1,2.
вычисленное приближенно с помощью
первого дифференциала приближенно
равно … Ответ 1,2.
Решение: пользуемся формулой приближенного
вычисления
![]() +
+
![]() ,
где
,
где
![]() .
При этом
.
При этом
![]() ,
y = 3,97, x0
= 1, y0 =4.
,
y = 3,97, x0
= 1, y0 =4.
![]()
13. Множество первообразных функции
![]() имеет
вид … Ответ:
имеет
вид … Ответ:
![]()
Решение:
![]() =
=
![]()
14. Среднее значение функции
![]() на отрезке
на отрезке
![]() равно … Ответ:
равно … Ответ:
![]() .
.
Решение: среднее значение находим по
формуле
![]() =
=
![]() =
=
![]() .
.
15. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет четное число очков, равна …. Ответ 0,5.
Решение: P(A) = m/n = 3/6 = 0,5, m = 3 – число благоприятных (2, 4, 6), а n = 6 – общее число исходов (1, 2, 3, 4, 5, 6).
16. Устройство состоит из двух элементов, работающих независимо. Вероятность их не отказа в работе 0,75 и 0,90. Найти вероятность, что оба элемента откажут. Ответ: 0,025.
Решение: По формуле произведения
независимых событий
![]()
17. Дискретная случайная величина задана законом распределения
|
x |
1 |
2 |
5 |
6 |
|
p |
0,1 |
a |
b |
0,3 |
Тогда a и b могут быть равны … Ответ: a = 0,4 b = 0,2.
Решение: из предложенных вариантов выбираем тот, где сумма в нижней строке равна 1.
18. 1 Дискретная случайная величина задана законом распределения
|
xi |
1 |
2 |
4 |
|
pi |
0,2 |
p2 |
0,3 |
Тогда ее математическое ожидание равно … Ответ: 2,4.
Решение: находим p2
= 1 - 0,2 – 0,3 = 0,5. Тогда математическое
ожидание находим по формуле
![]() 1,2
= 2,4.
1,2
= 2,4.
19. Из генеральной совокупности извлечена выборка объема n = 120, полигон частот имеет вид
Тогда относительная частота варианты xi =4 равна … Ответ: 0,375.
Решение. Если n – объем выборки, ni частота i – варианты, то wi = ni/n –относительная частота. Из примера находим n2 = 120 – 10-15-20-30=45. Находим w2 =45/120 =0,375.
20. Размах вариационного ряда 11, 12, 14, 14, 14, 15, 17, 18 равен… Ответ: 7.
Решение: Размах ряда находим по формуле R = xmax – xmin =18 -11 = 7.
21. Из генеральной совокупности извлечена выборка объема n = 20.
|
xi |
2 |
4 |
5 |
6 |
9 |
|
ni |
7 |
2 |
1 |
5 |
5 |
Тогда несмещенная оценка математического ожидания равна … Ответ: 5,1.
Решение: Несмещенная оценка находится
по формуле = (14+8+5+30+45)/20 = 5,1.
= (14+8+5+30+45)/20 = 5,1.
22. Дан доверительный интервал (18,44; 19,36) для оценки математического ожидания нормально распределенного качественного признака. Тогда точечная оценка математического ожидания равна … Ответ: 18,9.
Решение: точечная оценка соответствует середине доверительного интервала
(18,44 + 19,36)/2 = 18,9.
_________________________________________________________________________________23. Выборочное уравнение парной регрессии имеет вид y = 6,4 – 1,6x. Тогда выборочный коэффициент корреляции может быть равен…
Решение: он принадлежит сегменту
![]() и совпадает по знаку с выборочным
коэффициентом регрессии - 1,6. Поэтому
может быть равен -0,92.
и совпадает по знаку с выборочным
коэффициентом регрессии - 1,6. Поэтому
может быть равен -0,92.
24. Основная гипотеза имеет вид H0: a = 12. Тогда конкурирующей может являться гипотеза ...
Решение: конкурирующая т.е. противоположная
для имеющегося в основной гипотезе
равенства H1:
![]()
25. Область допустимых решений задачи линейного программирования задана многоугольником ОАВСД. Тогда максимальное значение функции F(x) = 2x1 + 3x2 достигается в точке …
Решение: выполняется графически.
Определяется вектор градиента функции
gradF =
![]()
Для заданной функции gradF = (2; 3) и находится последняя вершина многоугольника ОАВСД в направлении вектора градиента.
26. Транспортная задача будет закрытой, если «а» , «в» и «с» равны…
|
|
а |
60 |
в |
|
40 |
4 |
9 |
2 |
|
с |
10 |
7 |
8 |
|
30 |
12 |
3 |
5 |
Решение: задача будет закрытой, если 40 + с +30 = а + 60 + в, или а + в = с + 10. Из предлагаемых вариантов выбираем подходящий, например а = 40, в = 70, с = 100.
27. Матрица выигрышей в игре с природой имеет вид
 тогда средний выигрыш игрока по критерию
Байеса, относительно выигрышей будет
равен … Ответ: 8,0.
тогда средний выигрыш игрока по критерию
Байеса, относительно выигрышей будет
равен … Ответ: 8,0.
Решение: выбираем максимальное из чисел
![]() = 2х0,25 + 10х0,75 = 8,0
= 2х0,25 + 10х0,75 = 8,0
![]() = 6х0,25 + 8х0,75 = 7,5
= 6х0,25 + 8х0,75 = 7,5
![]() = 8х0,25 + 4х0,75 = 5,0
= 8х0,25 + 4х0,75 = 5,0
![]() = 12х0,25 + 2х0,75 = 4,5
= 12х0,25 + 2х0,75 = 4,5
28. Для сетевого графика, изображенного на рисунке

длина критического пути равна…
Варианты ответов:
1) 40, 2) 12, 3) 13, 4) 30.
Решение: Наиболее протяженный
путь по времени называется критическим
путем. В задаче наиболее протяженным
является путь
![]() ,
его длина равна 4+11+15 = 30.
,
его длина равна 4+11+15 = 30.
Ответ: 4)
29. Функция
полезности потребления имеет вид
![]() .
Тогда при
.
Тогда при
![]() предельная
норма замещения продукта X продуктом
Y
предельная
норма замещения продукта X продуктом
Y
 равна
…
равна
…
Варианты ответов:
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() .
.
Решение:
![]() .
.
Ответ: 3)
30. Дана функция полезности
![]() .
Тогда кривая безразличия задается
уравнением…
.
Тогда кривая безразличия задается
уравнением…
Варианты ответов:
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() .
.
Решение: Кривая безразличия задается
уравнением
![]() .
.
31. Дана функция полезности
![]() .
Тогда кривая безразличия задается
уравнением…
.
Тогда кривая безразличия задается
уравнением…
Варианты ответов:
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() .
.
Решение: Кривая безразличия задается
уравнением
![]() .
.
32. Объем промежуточной продукции в линейной статистической модели Леонтьева представлен матрицей

